中性面对倾覆力矩中心和倾覆力矩臂的影响

何为中性面呢？可利用图3-2来说明这个问题：若在图的左上端施加一个垂直于地面的载荷，右端必然翘起来，反之若载荷施加于右上端，左端又必然翘起来。若载荷沿着簧载质体平移，当质体只作平上平下运动之处，便是所求之中性面，因此，多簧质量系统的中性面，就是这样一个面，若沿此面作用一个垂直负荷时，系统各簧的变形相等。对于汽车来说，中性面也就是倾覆力矩中心所在的平面。因此，只有知道了中性面的位置，才能确定倾覆力矩中心的位置以及倾覆力矩臂的大小。这对于研究车身稳定性和平顺性等均是十分重要的。

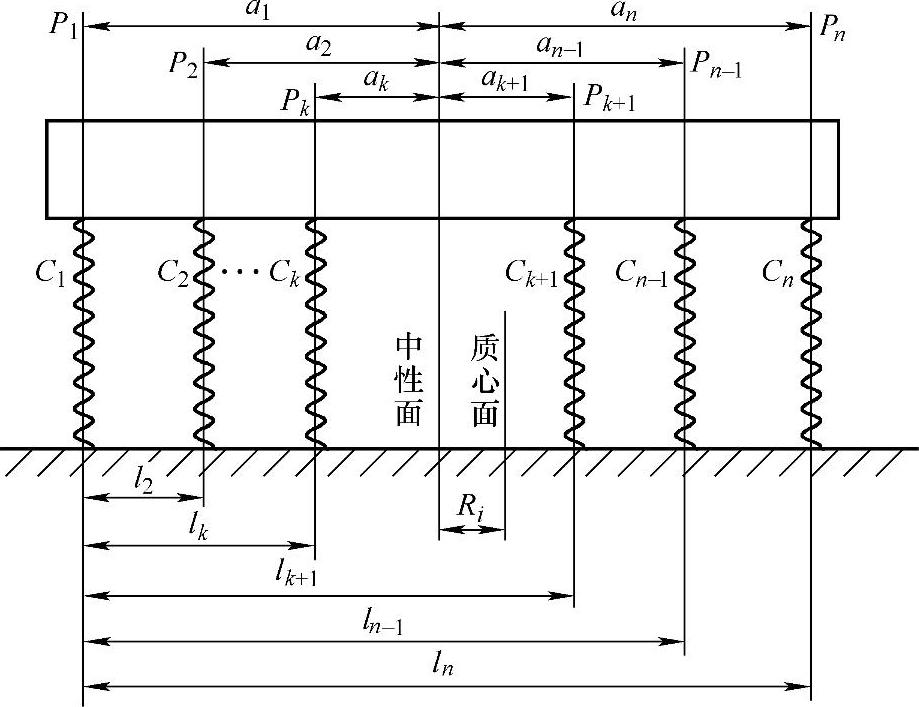
图3-2 中性面的位置

首先确定第一簧至中性面的距离a₁。

设中性面在k和k+1个弹簧之间，k为1至（n-1）中的任意整数。假设在中性面处作用一垂直载荷P时，各簧的变形力为P_i。由于系统在中性面处的组合线刚度C₀等于各簧线刚度C_i之和，即

再根据此时各簧变形相等的特点，便有

于是各簧变形力为

现假设各簧至中性面的距离为a_i，根据各簧对中性面所取力矩之和为零的关系可得

将式（3-11）代入式（3-12）后便有

在图3-2中，假设各簧至第一簧的距离为l_i，按其几何关系有

a_i=a-l_i（3-14）(www.xing528.com)

把式（3-14）代入式（3-13）后可解得第一簧至中性面的距离：

式中 a₁——第一簧至中性面的距离（mm）；

C_i——各簧线刚度（N/mm）；

l_i——各簧至第一簧的距离（mm）。

再确定任一簧至中性面的距离a_x。

式（3-15）虽已完全确定了中性面的位置，然而，这并非一般表达式，在一定的情况下，尚需知道各簧至中性面的距离。由图3-2的几何关系可知：

a_x=a₁-l_x （3-16）

将式（3-15）代入式（3-16）可解得

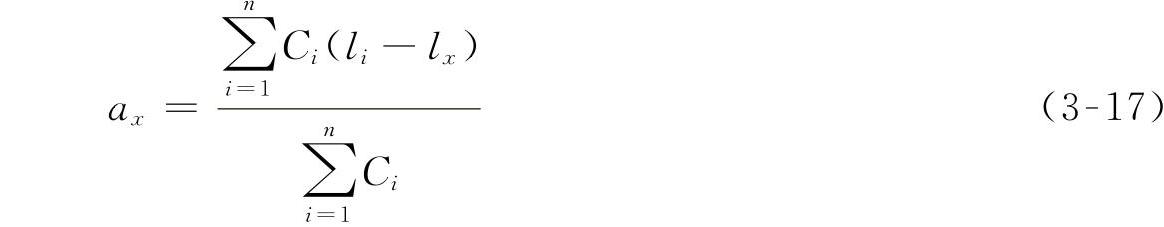
式中 a_x——任一弹簧至中性面的距离（mm）；

l_x——任一弹簧至第一簧的距离（mm）。

式（3-15）和式（3-17）的物理概念是鲜明的。若将它们的分子、分母同乘以各簧的变形f_i，均可转化为一个力矩平衡式。

式（3-17）的值可正可负，是对中性面位置的方位描述：当计算数值为正时，说明中性面在该（x）簧右侧；计算数值为负时，说明中性面在该（x）簧左侧。