动车组噪声控制技术：车内外噪声仿真预报

5.3.4.1 统计能量法基本理论

（1）统计能量分析的基本假设 统计能量分析方法认为一个机械系统或流体系统都可以借助一系列的子结构来构成系统分析模型，其中，每个子结构都是包含许多模态的振荡器。在建立统计能量分析模型时，有以下普遍的基本假设：

1）模型中的各子结构之间的耦合是线性、守恒的耦合，即这些耦合都是弹性耦合、惯性耦合或回转力耦合，不存在非保守性质的耦合特征。

2）能量在所研究的频带内具有共振频率的子结构之间流动。

3）系统所受的力为互不相关的宽带随机激励，这些随机激励在统计上是独立的，所以具有模态非相干性，并可以应用能量的线性叠加原理。

4）在给定的子结构中，在给定频带内所有共振模态之间的能量是等分。

表5-23 气动噪声功率谱参数值

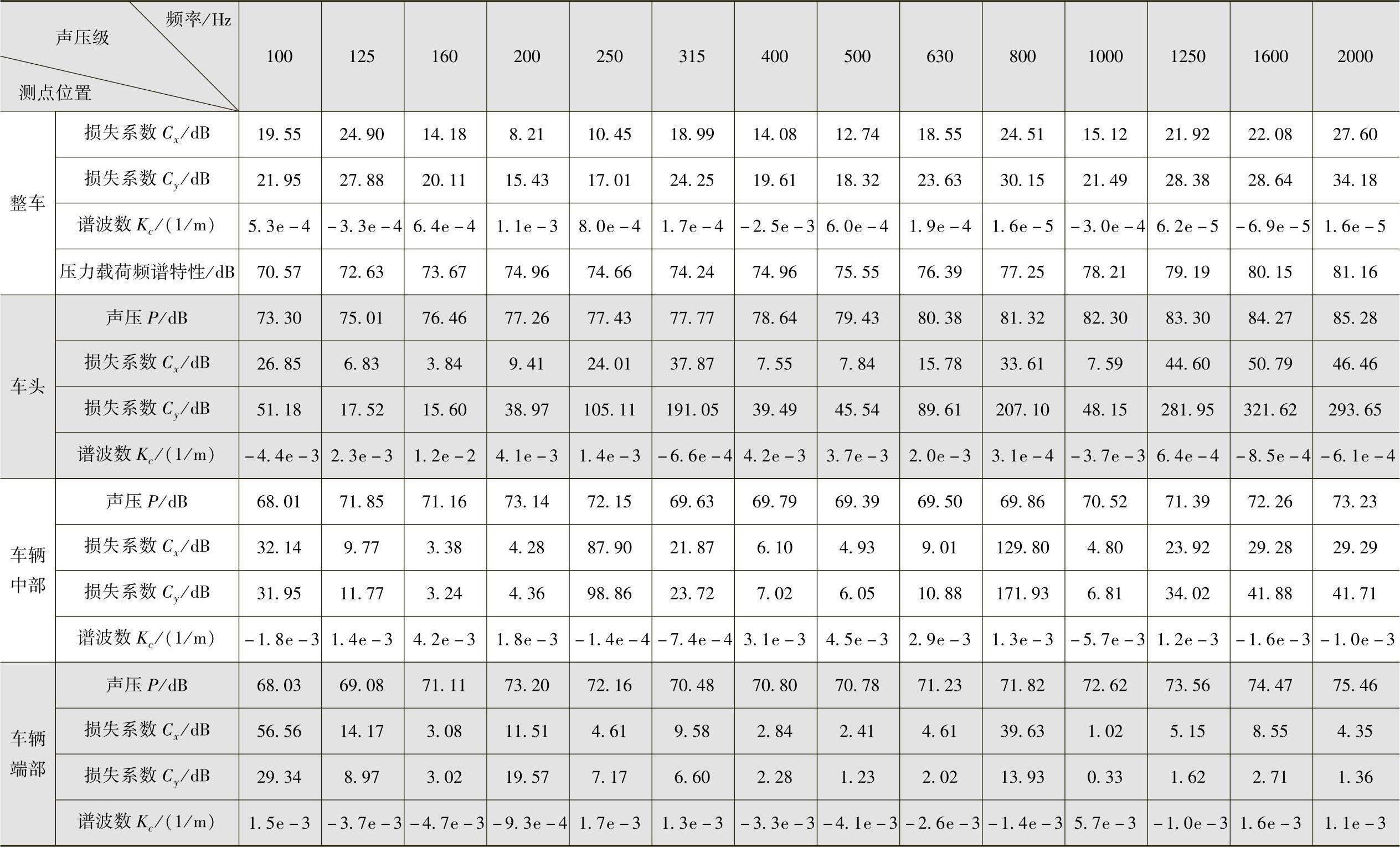
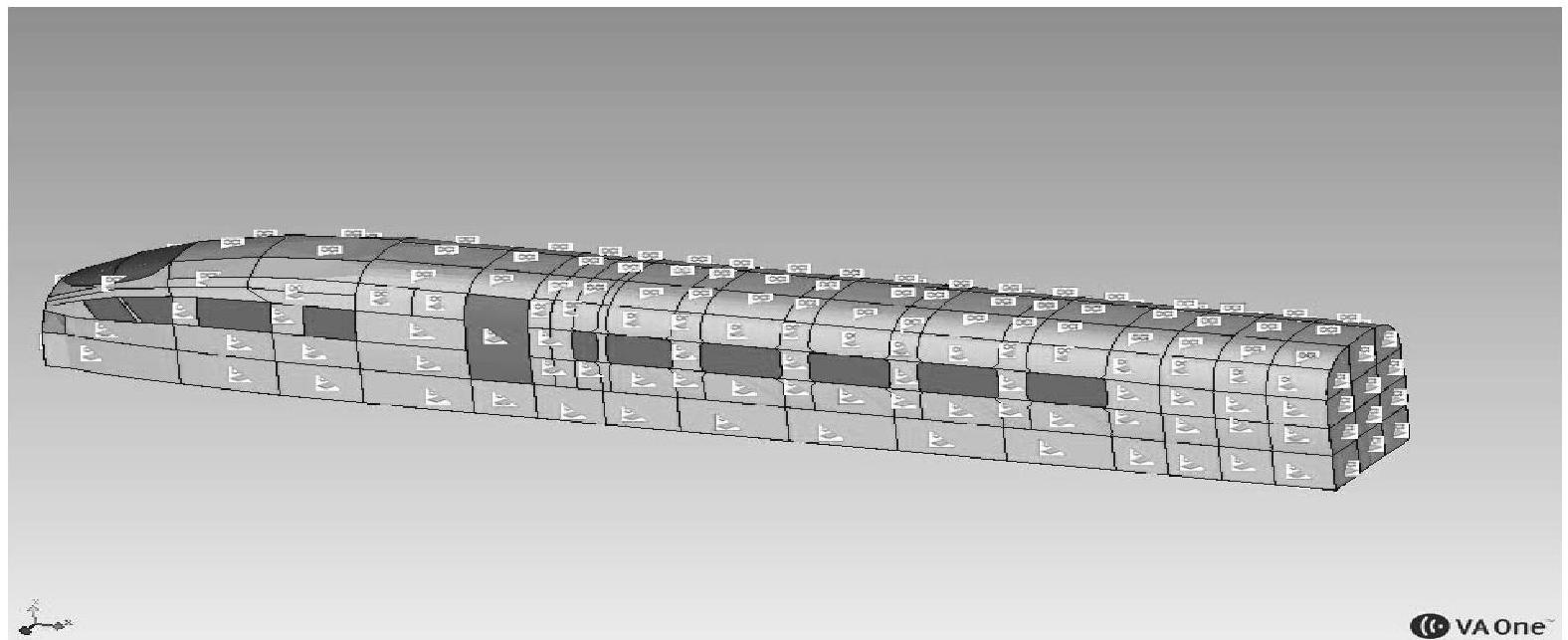
图5-133 车体湍流边界载荷

5）互易性原理适用于不同子结构间。

6）任两个子结构间的能量流与振动时耦合的子结构间的实际能量差成正比。

（2）统计能量分析的适用范围 根据统计能量分析模型中每个子系统模态密度n（f）的大小和带宽Δf内振型N=n（f）×Δf的多少，把研究对象的频率范围划分为低频区、中频区和高频区：

1）当N≤1时，定义为低频区。

2）当1＜N＜5时，定义为中频区。

3）当N≥5时，定义为高频区。

统计能量分析适用于解决高频区内的复杂系统动力学问题。

（3）统计能量分析基本理论框架 对如图5-134所示单自由度振动系统，系统的耗散功率P_d为

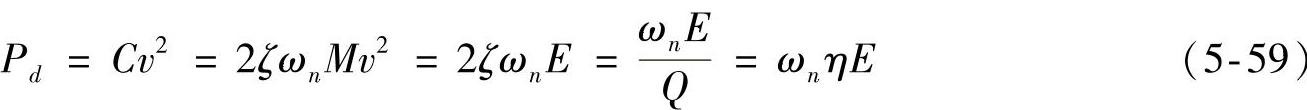
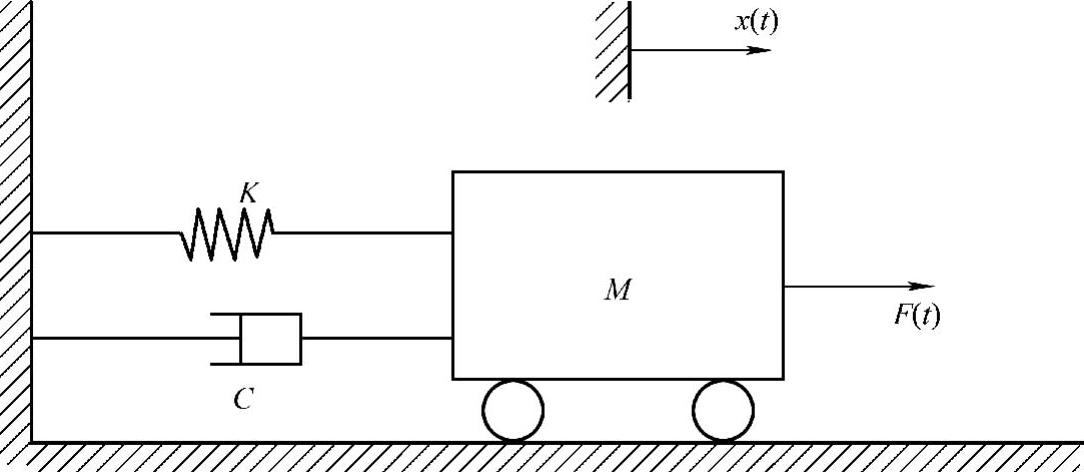
图5-134 单自由度振动系统

式中，C为振动系统的阻尼系数，υ为速度，ζ为阻尼比，n为系统固有频率，M为振动系统质量，E为振动系统能量，Q为品质因子，为系统内损耗因子。推广至一定频带宽内的一系列单自由度系统组成的一般子结构，有

式中，ω为频带的几何平均中心频率，η为对应该频带内所有模态的平均损耗因子。

以两个子结构组成的最简单的统计能量模型为例，如图5-135所示，建立其功率平衡方程。

由功率流平衡关系，可得

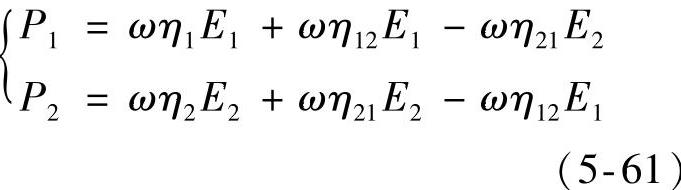
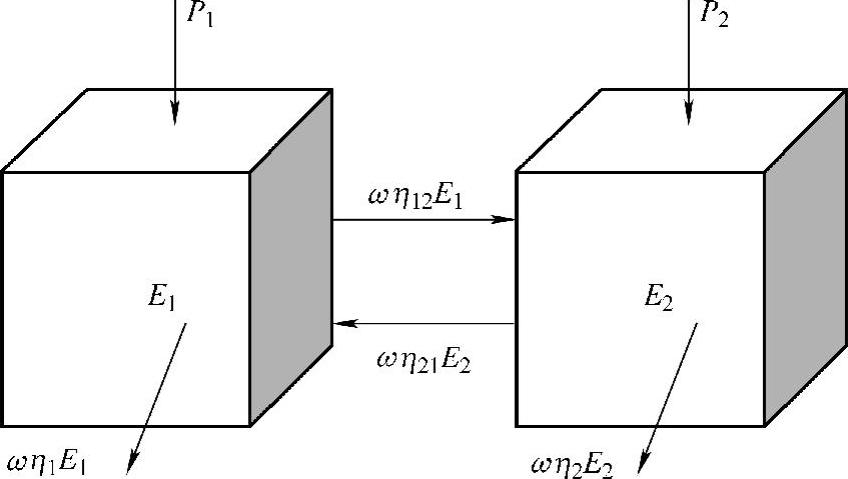
图5-135 简单的统计能量分析模型

在保守耦合情况下，由线性、无源和可逆子系统构成的大系统，都存在互易性普遍原理。统计能量分析中的互易性原理为

n_iη_ij=n_jη_ji （5-62）

式中，n_i，n_j分别为子系统i、j的模态密度，ij、ji分别为振动能量从子系统i传至子系统j的耦合损耗因子和振动能量从子系统j传至子系统i的耦合损耗因子。

因此，利用互易性原理，计算方程可表述如下：

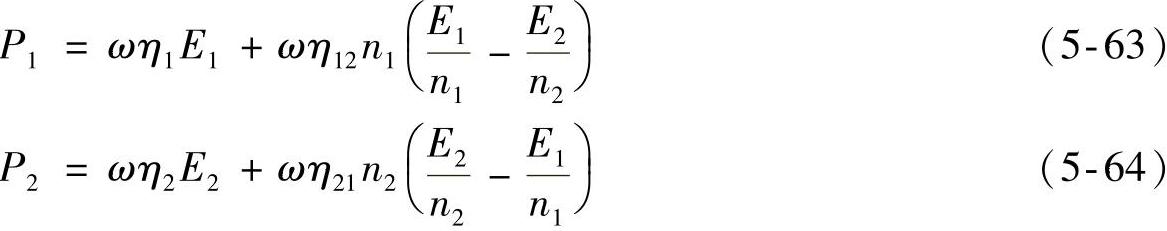
写成矩阵形式，有

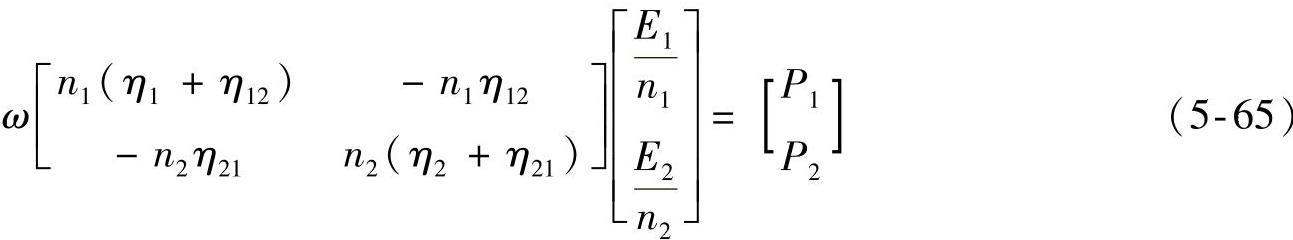
系统的损耗因子、输入功率都可通过理论计算或试验测试获取，这时，通过求解式（5-65）就可解出所需各子系统的平衡能量水平。推广至包含N个子系统的复杂动力学系统，其能量平衡方程：

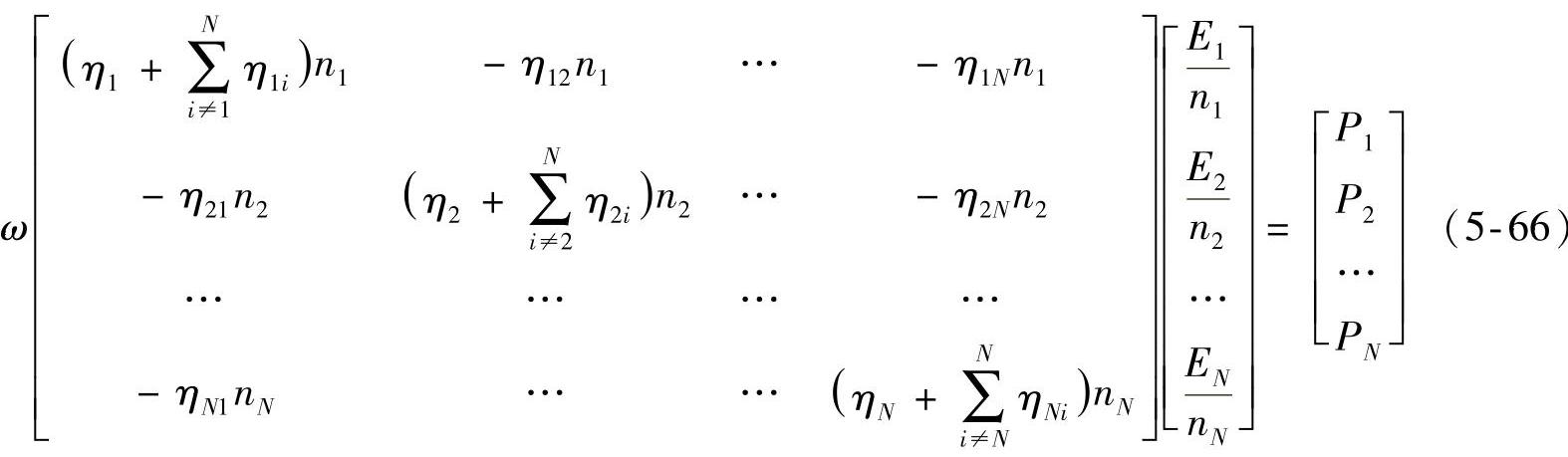
或

ω[L][E]=[P] （5-67）

式中，[L]为包含内损耗因子和耦合损耗因子的系统能量损耗矩阵，具体为

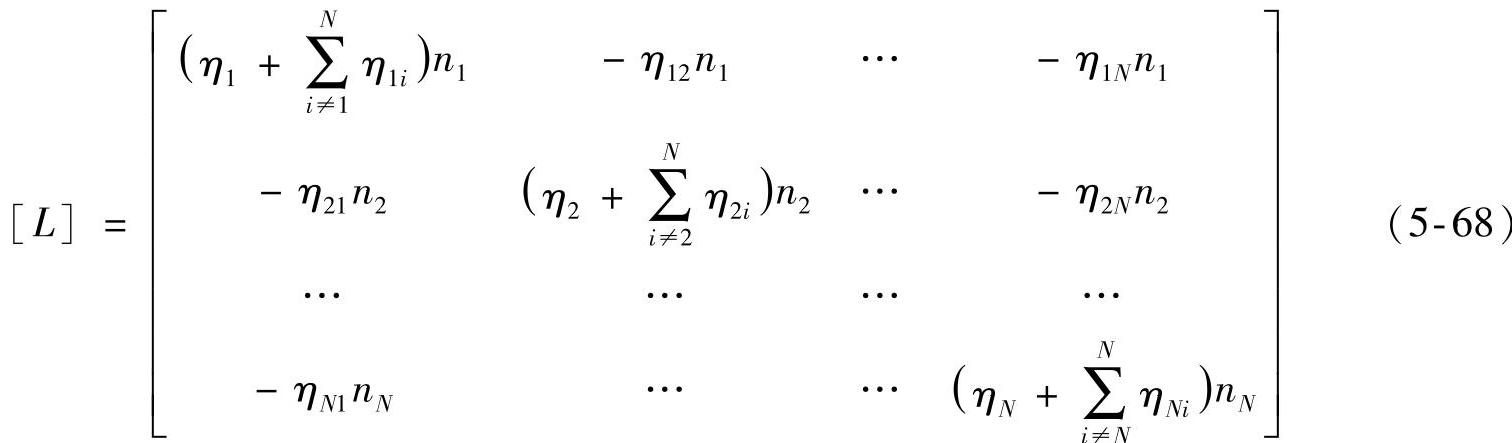
[E]为子系统能量矩阵，[P]为系统输入功率矩阵，具体表达式分别为

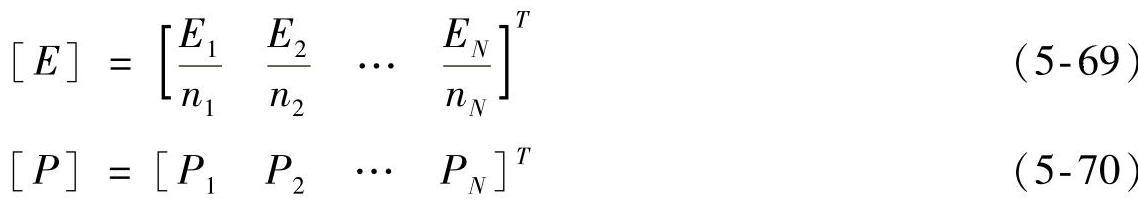
式（5-67）～式（5-70）代表了利用统计能量分析法对复杂系统进行分析的最基本表达式。方程中包含的统计能量分析参数包括：模态密度、内损耗因子、耦合损耗因子以及输入功率。如果具备这些参数，求解联立方程，即可得到每个子系统上总的能量。再根据如下的能量定义式：

式中，M为结构子系统的质量；〈v²〉为时间平均和空间平均的均方振动速度；M〈v²〉为结构子系统的能量；V为声学子系统的体积；〈p²〉为时间平均和空间平均的均方声压；ρ为介质密度；c为声音在介质中的传播速度；V〈p²〉/c²为声场子系统的能量。

系统的模态密度、内损耗因子、耦合损耗因子以及输入功率都可通过理论计算或试验获取，通过这些参数和输入功率，可以求出目标子系统的平均能量水平，从而进一步转换成所需要的振动级、声压级、应力等动力学参数。

（4）统计能量分析子系统划分原则 统计能量分析之所以能够为受高频宽带激励的复杂工程结构系统提供动力学计算响应预测，就是因为它能够把复杂系统（包括机械的和声学的系统）划分为不同的模态群，并且在统计意义上把大系统分解成便于分析的独立子系统，而不是逐个精确地确定每个模态的响应。在工程结构初步设计阶段应用统计能量分析的第一步就是定义出模态群构成的子系统，所建立的统计能量分析模型必须能够清楚地表示出振动能量的输入、存储、损耗和传输的特征。

统计能量分析中的子系统是可存储能量的子系统，而只有一些相似共振模态组成一群共振运动的子系统才可能存储振动能量。因此，一群相似共振模态就可视为一个子系统。一个子系统在分析带宽内的模态数，是由子系统的特征参数模态密度确定的。所以目前建立统计能量分析模型子系统的一条重要原则就是子系统模态密度必须足够高。有研究表面，分析带宽能的模态数须超过5才能保证计算结果有效。

模态相似的准则是振型要用相同的动力学特性（即相同的阻尼、相同的模态能量和相同的耦合损耗因子等）。通常根据复杂结构耦合系统的自然边界条件、动力学边界条件、材料介质特性以及上述的原则建立子系统。同时，还要根据实际情况、任务阶段要求和经验建立统计能量分析模型。

（5）统计能量分析基本参数 由式（5-67）～式（5-70）可知，统计能量分析模型所需的基本参数是系统的模态密度、内损耗因子和耦合损耗因子。利用这些基本参数，结合统计能量分析模型的输入功率，通过对所建统计能量分析模型进行分析计算，就可以求出目标子系统的平均能量水平，从而进一步转换成所需要的振动级、声压级、应力等系统响应结果。因此，模态密度、内损耗因子和耦合损耗因子，这些参数对SEA的计算精度起着决定性的作用。这些参数的确定可以通过理论计算或通过试验方法测量，可以根据工程设计的不同阶段和分析的不同目标，采取更适合的方法进行确定。

1）模态密度。统计能量分析中的模态密度是描述振动系统贮存能量能力大小的一个物理量。理论确定模态密度基本上是个数学问题，首先从系统的振动方程得到频率方程，然后找到用频率表示的共振频率数的数学表达式，再将其数学式对频率取微分就可得到模态密度的计算公式。

2）内损耗因子。内部损耗是指由系统阻尼特性所决定的那部分能量损耗，所以内损耗因子有时也称作阻尼损耗因子。可将内损耗因子写为

内损耗因子是指子系统在单位频率内单位时间损耗能量与平均存储能量之比。工程中，对系统阻尼特性的描述参数有很多，它们与统计能量分析中的内损耗因子之间的关系见表5-24。

表5-24 各种阻尼参数与内损耗因子η的关系

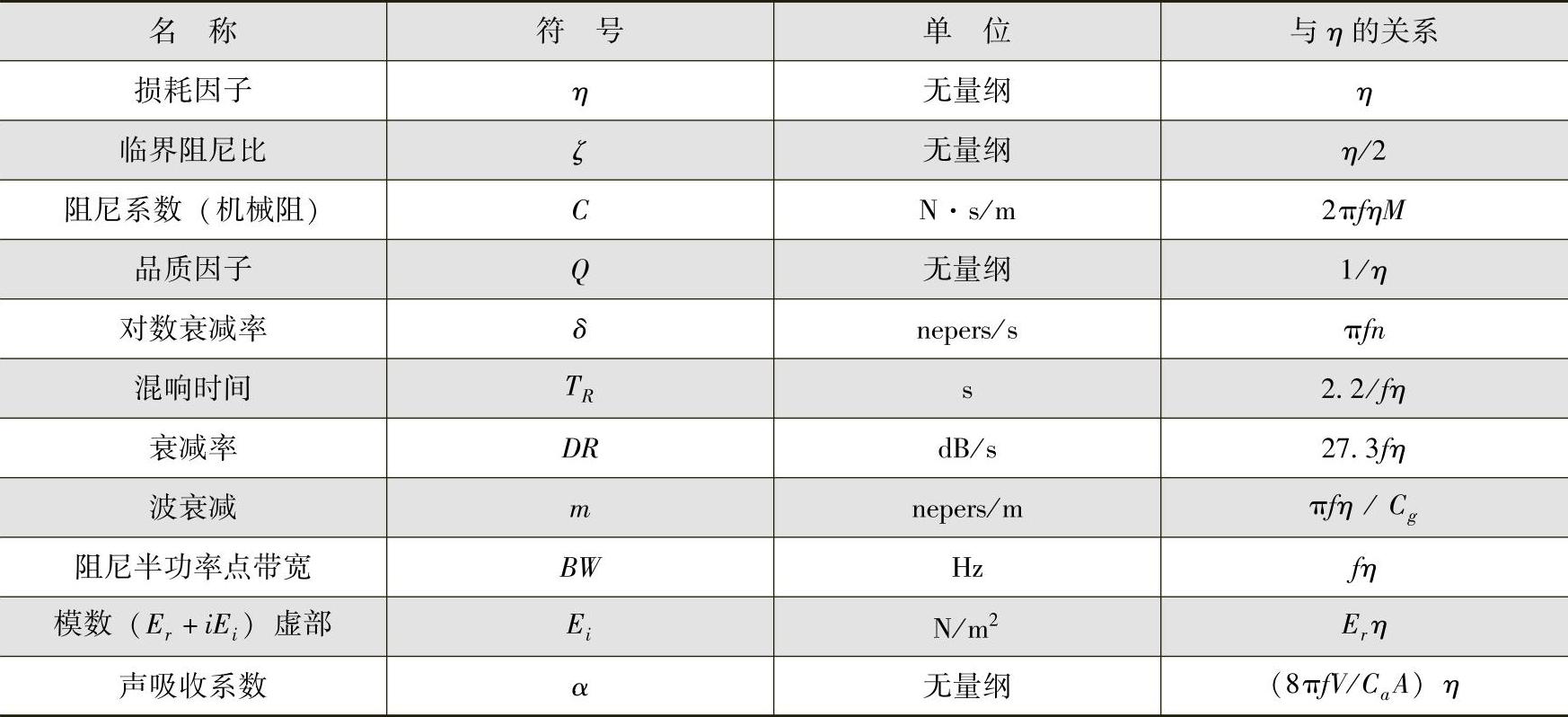
表5-24中，C_g为系统群速度（m/s），M为系统质量，A为表面积，V为声腔容积，C_a为空气中的声速。

在机械结构中，子系统的内损耗因子主要是由三种彼此独立的阻尼机理构成的，其关系式为

η_i=η_is+η_ir+η_ib （5-73）

式中 is——结构损耗因子，是子系统本身材料内摩擦构成的；

ir——声辐射损耗因子，是子系统振动声辐射阻尼形成的；

ib——边界连接损耗因子，是子系统边界连接阻尼构成的。

在统计能量分析对振动和噪声问题的实际应用中，有下面的简化估计：

①当子系统结构间为刚性连接时，ib＜s，此时i=is+ir，当子结构间为非刚性连接时，ib是不能忽略的。

②对于梁结构子系统，认为声的辐射损耗可以忽略不计，此时i≈is。

③当子系统为具有高辐射比ir的孤立单个轻质结构时，有is＜ir，此时i≈is；当不是轻质结构时，i≈is；当f＞fc或f＞fr（柱壳环频率）时，ir≈1.0，1r→0，此时i≈is。

经验表明，在非常低的频率区域，内损耗因子以结构损耗因子is为主；在低频和中频区域，内损耗因子以声辐射损耗因子ir为主；在高频区域内损耗因子又以结构损耗因子is为主。因此内损耗因子的下限是结构损耗因子is。

（6）传统噪声预测分析法的局限性 传统的数值计算方法如有限元法和边界元法在强度和振动计算方面取得很大成功，但在噪声预测方面存在一定的局限性。传统数值方法结构建模的精度在大约20阶模态后较低，特别是存在螺栓和点焊连接时，精度将进一步下降。而重要的声学频率范围常常超过100阶模态。基于上述原因，在航空工业的高频振动、高频噪声预测方面引进了统计能量分析技术。准确的统计能量分析方法依赖于结构的高模态密度（单位频带内的模态数）、高模态重叠度（共振峰值和频带宽的比率）和短波波长。然而，高模态密度、高模态重叠度和短波波长恰好是造成传统数值方法不精确和计算量大的因素。从根本上说，统计能量分析技术和传统的有限元或边界元数值方法在结构的全频段振动噪声预测方面相互补充。传统数值计算方法主要适用于低频，统计能量分析方法适用于高频。列车车内噪声的传统数值预测模型受到以下几个方面的限制：

1）在高频分析中，由于短波分辨率要求，需要对结构划分庞大的网格数量，使得计算量巨大。

2）对板件施加有限频带、散布压力场非常困难。

3）对车体（地板、侧墙、顶板等）板材以及内装结构的建模非常困难。

4）数值仿真周期长，不能满足我国轨道交通车内噪声的设计周期要求。

相比之下，统计能量分析把复杂结构动力学系统的模态参数（频率、振型、阻尼等）处理成随机变量，其预测结果不能提供系统某个局部位置的精确相应，却能从统计意义上较精确地预测出各个子系统的响应级。在工程结构的初步设计阶段，在工程人员尚未掌握研究对象的详细参数的情况下，能对系统的动力学性能进行预测。随着对被分析系统的细节参数了解增多，计算模型会逐步完善，动力学预测结果就会更精确。

（7）统计能量分析的特点 统计能量分析具有一种独特的建模方法。它以梁、杆、板、壳、柱等子结构为建模基础，搭建复杂系统的振动和噪声耦合动力学预测模型。统计能量分析的“统计”指的是所有系统子结构参数或总体参数都是在时间、空间和频率上经过统计平均处理的。例如，描述子结构能量消耗特性的内部损耗因子是在子结构上许多点测量的平均结果；描述子结构能量接受特征的模态密度则是在频带宽内平均的一种参数。正因为如此，用这种方法对振动水平进行的分析，其结果也必然是一种平均值，需要从统计的意义上去理解。

统计能量分析中的“能量”指的是系统中各个子系统间的相互联系是通过功率流描述的。模型的外界输入以输入功率流的形式进入系统，而输出结果也以子结构的输出功率流表示。系统各子结构间的功率流动存在一定的规律性。各能量由高内耗子结构向低内耗子结构流动，能量由低模态密度子结构向高模态密度子结构流动。当然，能量流动方向还取决于子结构间的耦合特性。

统计能量分析中的“分析”则指的是它是一种建模方法，是一种理论预测方法，具有一切“分析”方法的所有特征，如模型的建立、模型的参数确定、求解系统方程得到所需要的解等。但是较为独特的是该模型中许多参数需要通过实验取得，特别对复杂子结构更是如此。(www.xing528.com)

由于统计能量分析方法的上述特性，它也具有一定的局限性。主要表现为：

1）按目前的统计能量分析发展水平，适用于解决高频区内复杂结构的动力学问题，而不适用于解决中低频问题的分析。但是，采用与有限元混合建模的技术，可以有效地解决中高频问题。

2）因为统计能量分析所有参数都是时、空、频域的平均统计量，所以分析结果不能得到某一特定位置处的响应结果。也就是说，统计能量分析不能预测系统中某局部位置的精确响应，但能准确地从统计的意义上预测整个子结构的平均响应。它几乎是目前唯一能预测复杂系统对高频宽带随机激励响应的实用分析方法。

5.3.4.2 基于SEA的车内噪声预报

（1）头车模型建立 采用统计能量分析理论（SEA方法）进行建模，建模时主要把握以下原则：

1）频率100～4000Hz内，模型中每个子系统带宽内的模态数大于1。

2）子系统划分原则：与车下设备激励源的尺寸相对应。

3）模型中，局部子系统模态数不能达到要求，但因尺寸较小，计算结果对整体结果影响可以忽略不计。

4）考虑到车体尺寸，车内声腔划分为三层，车体横向划分为三个，可以提高1.5m处噪声计算精度。

5）针对不同材料属性（如车门、车窗部位），单独划分为板单元。在所建好的模型中任取一块板模型和一个腔体，计算后由VAone得出，如图5-136、图5-137所示。

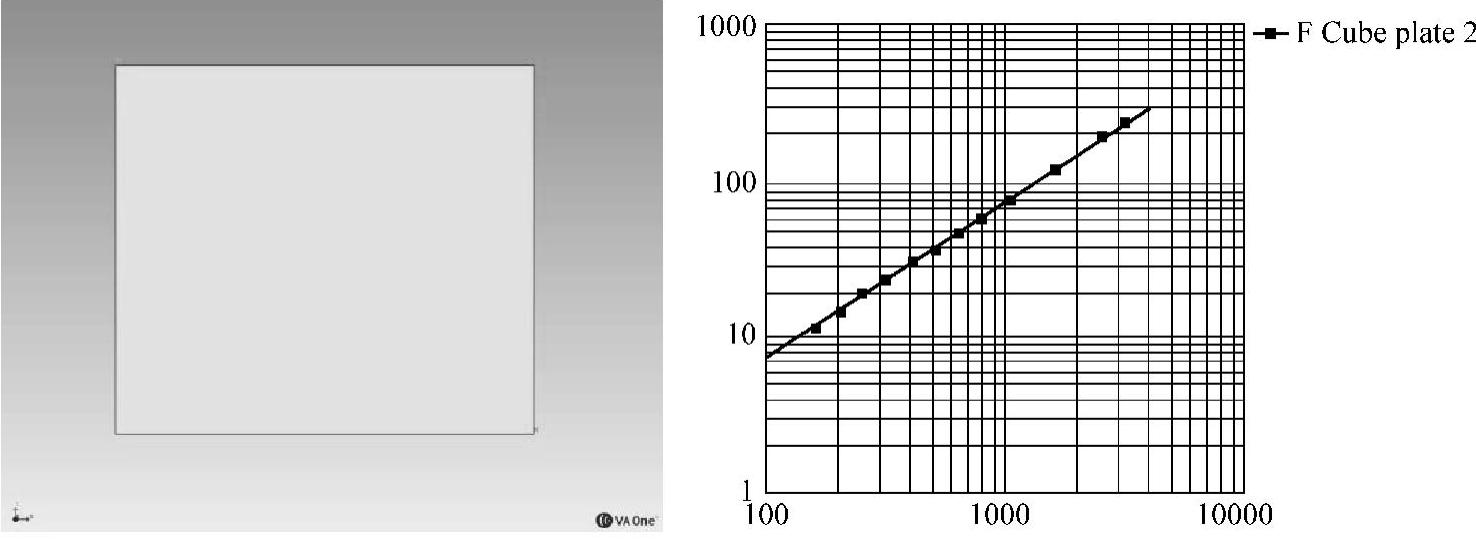
图5-136 SEA板模型及带宽（mode in band）

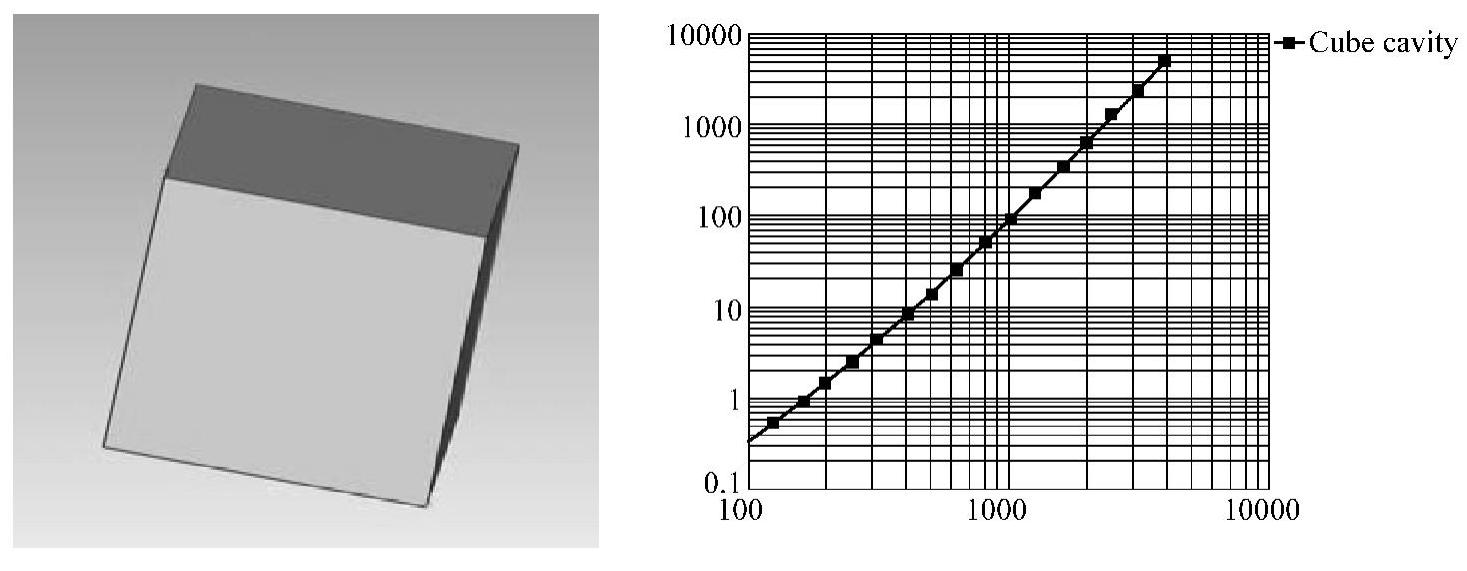
图5-137 声腔模型及带宽（mode in band）

以上从模型中任意选取比较常规的声腔和板，从图中可以看出最小带宽在分析的频段内模态数大于1的要求。

（2）载荷获取 基于上述隔声仿真计算结果、轮轨仿真计算、气动噪声计算结果作为基本输入载荷。计算流程如图5-138～图5-141所示。

（3）车内噪声计算结果 车内噪声计算分为车辆静止（设备全开）和运行300km/h工况。车内选点情况如图5-142、图5-143所示。

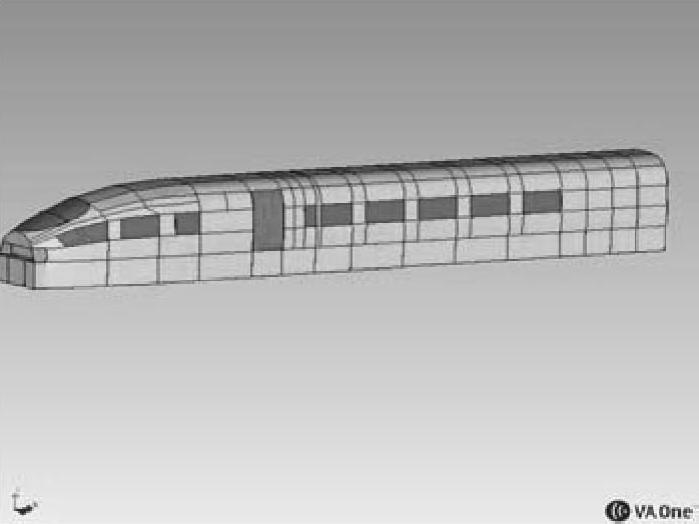
图5-138 头车SEA车体子结构一

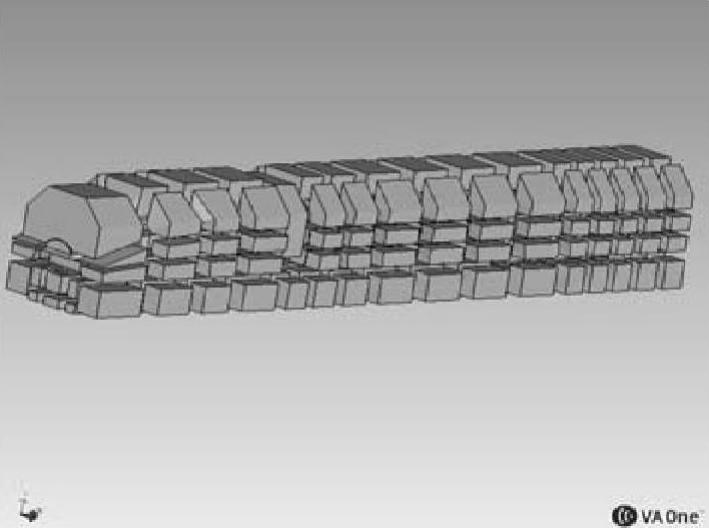
图5-139 头车SEA车体子结构二

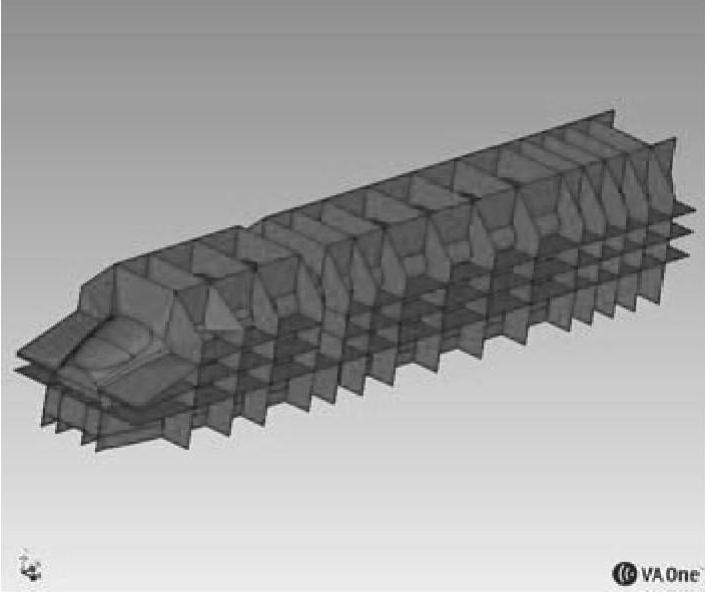
图5-140 头车模型面连接

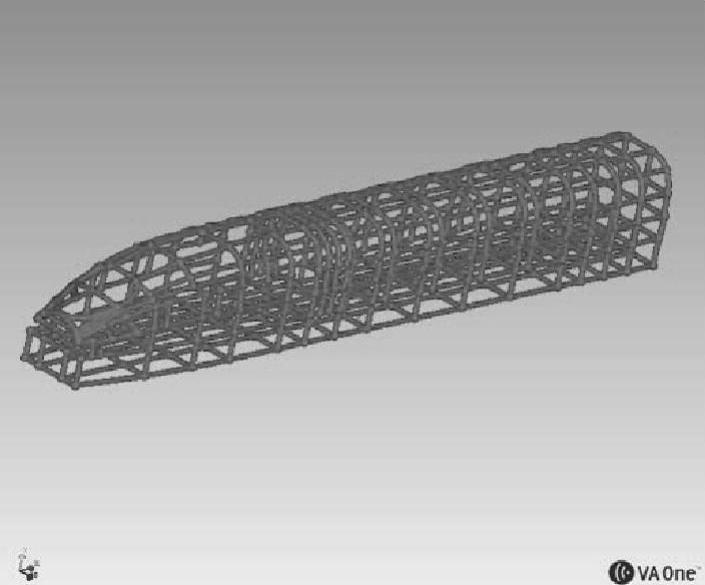
图5-141 头车模型线点连接

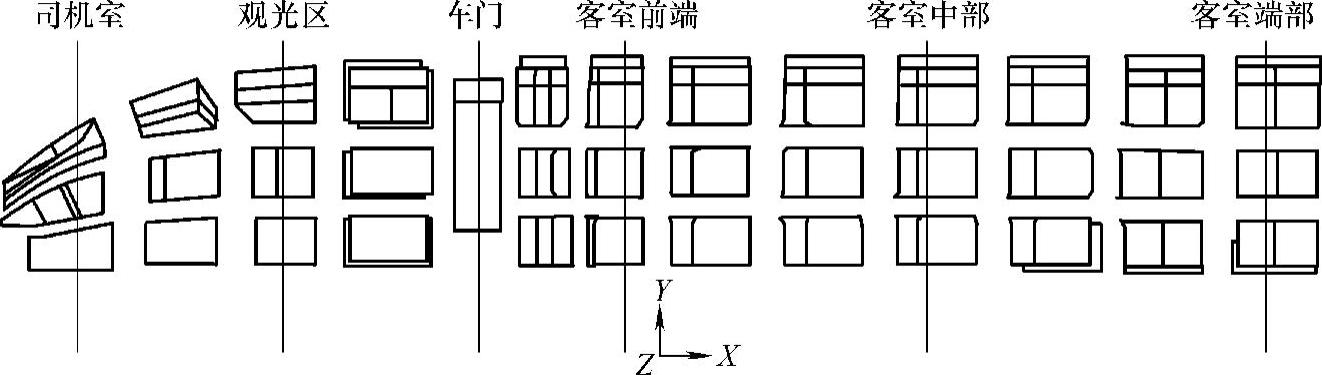
图5-142 车内选点名称（选取第二层中间声腔即为1.5m处）

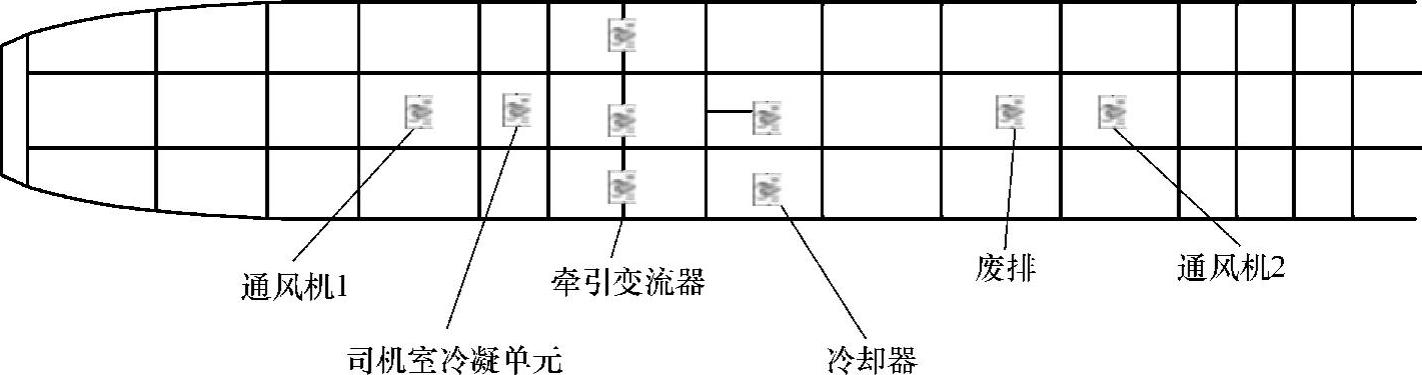
图5-143 车内选点名称（选取车下设备载荷位置车内0.5m处声腔第三层）

车辆静止（设备全开）计算结果如图5-144～图5-147所示。

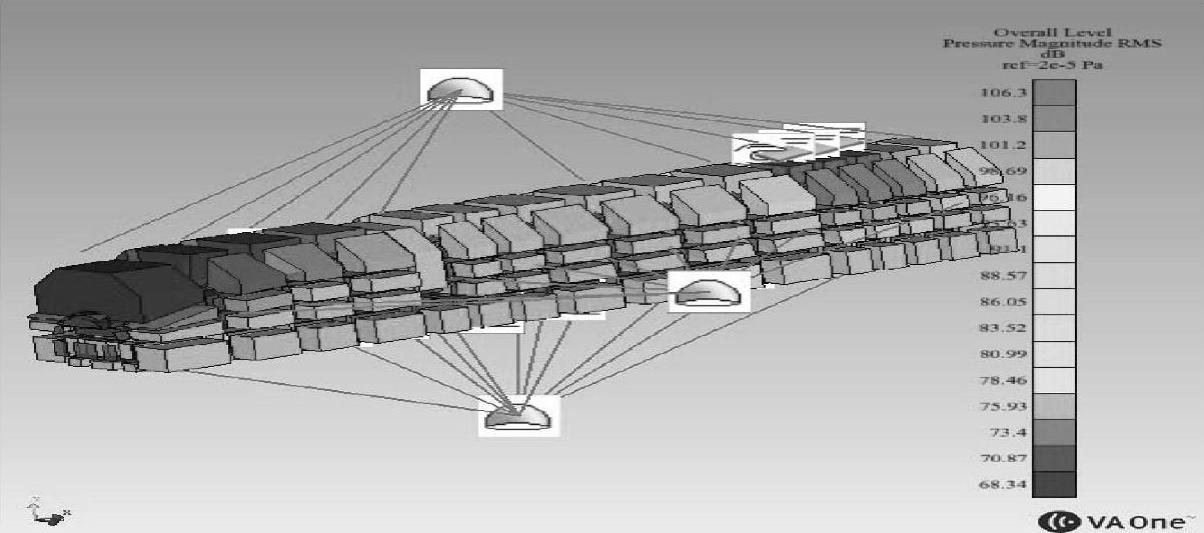
图5-144 静止车内外声压级

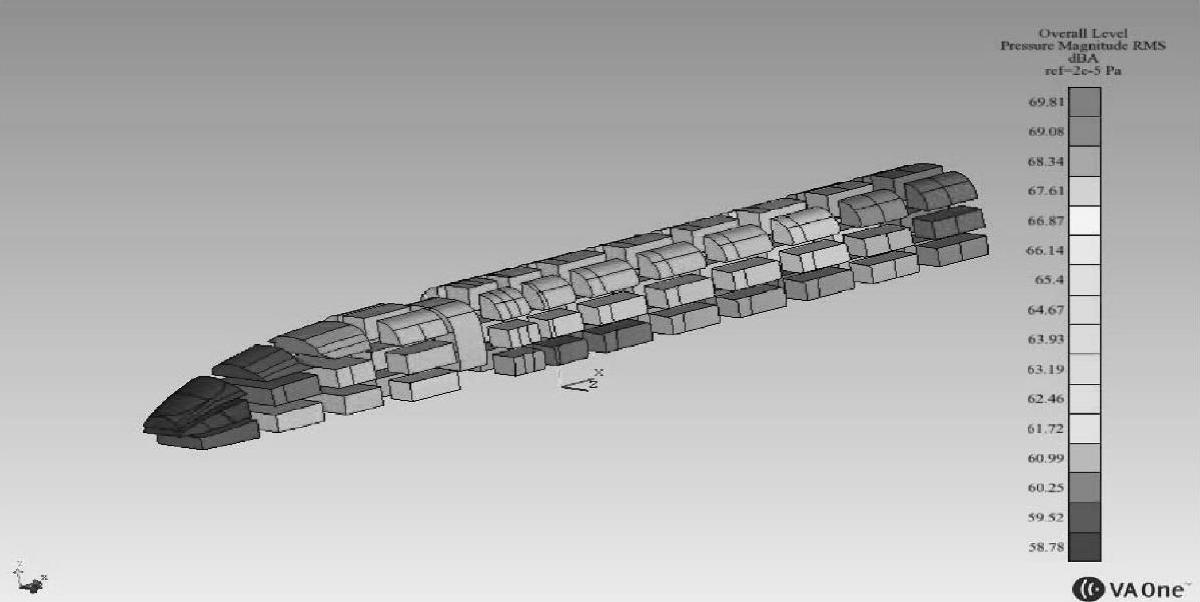
图5-145 车静止工况车内噪声

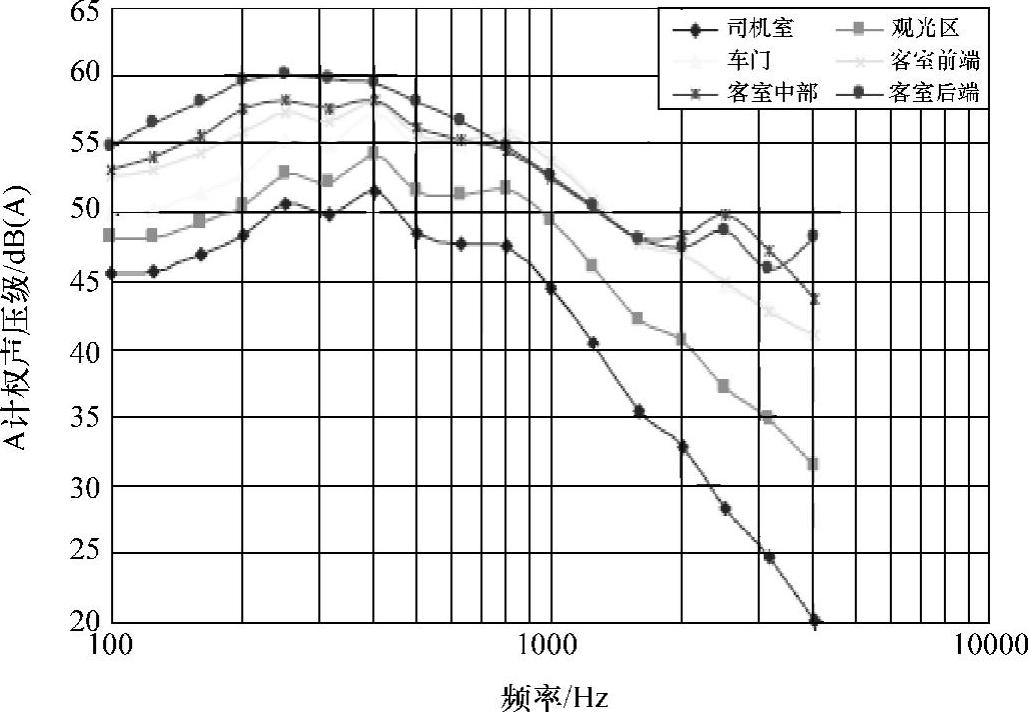
图5-146 车内地板1.5m处噪声值

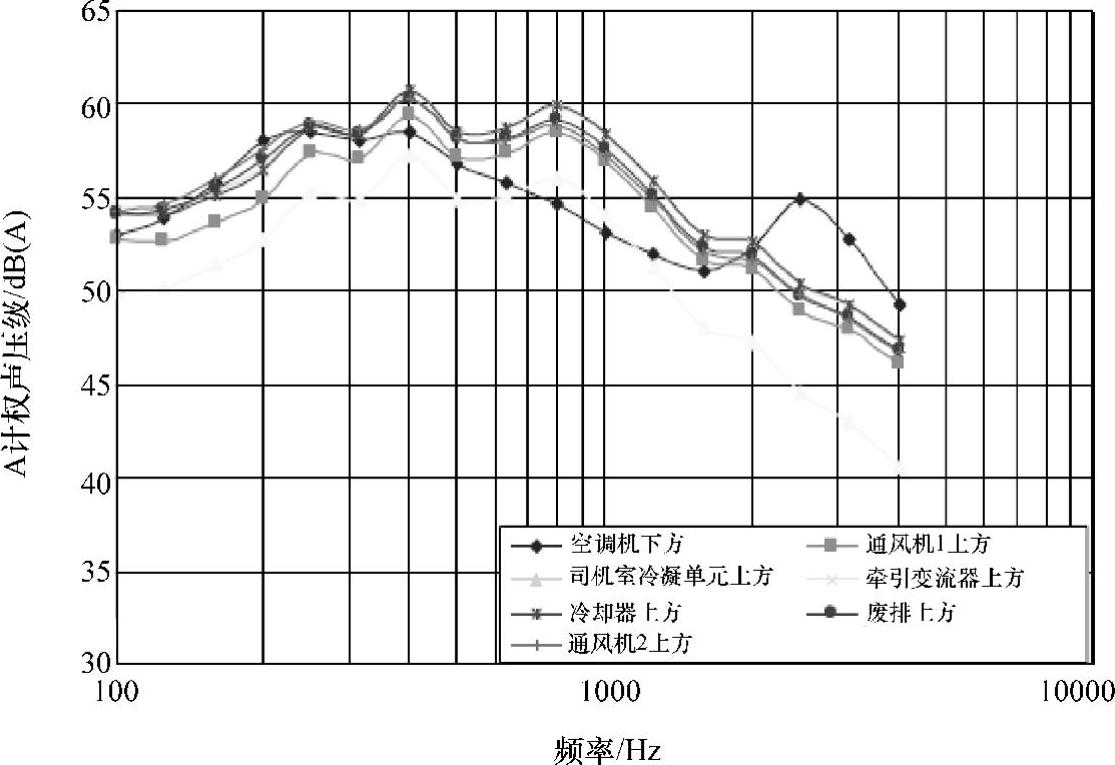
图5-147 车内设备上方0.5m处噪声值

运行工况300km/h计算结果如图5-148、图5-149所示。

从云图中可以看出噪声值在转向架下方比较大，其次是车头部位和端部受到气动噪声影响噪声比较明显，然后是有源设备下方处。整个结构声压级变化趋势比较合理。

5.3.4.3 车外噪声仿真预测

RAYNOISE是比利时声学设计公司开发的一种大型声场模拟软件系统。其主要功能是对封闭空间或者敞开空间以及半闭空间的各种声学行为加以模拟。它能够较准确地模拟声传播的物理过程，包括镜面反射、扩散反射、墙面和空气吸收、衍射和透射等现象。该系统可以广泛应用于厅堂音质设计、工业噪声预测和控制、录音设备设计，以及机场、地铁和车站等公共场所的语音系统设计，还有公路、铁路和体育场的噪声估计等。RAYNOISE不仅有良好的界面，还具有较高的计算速度和精确度。RAYNOISE系统工作框图如图5-150所示。

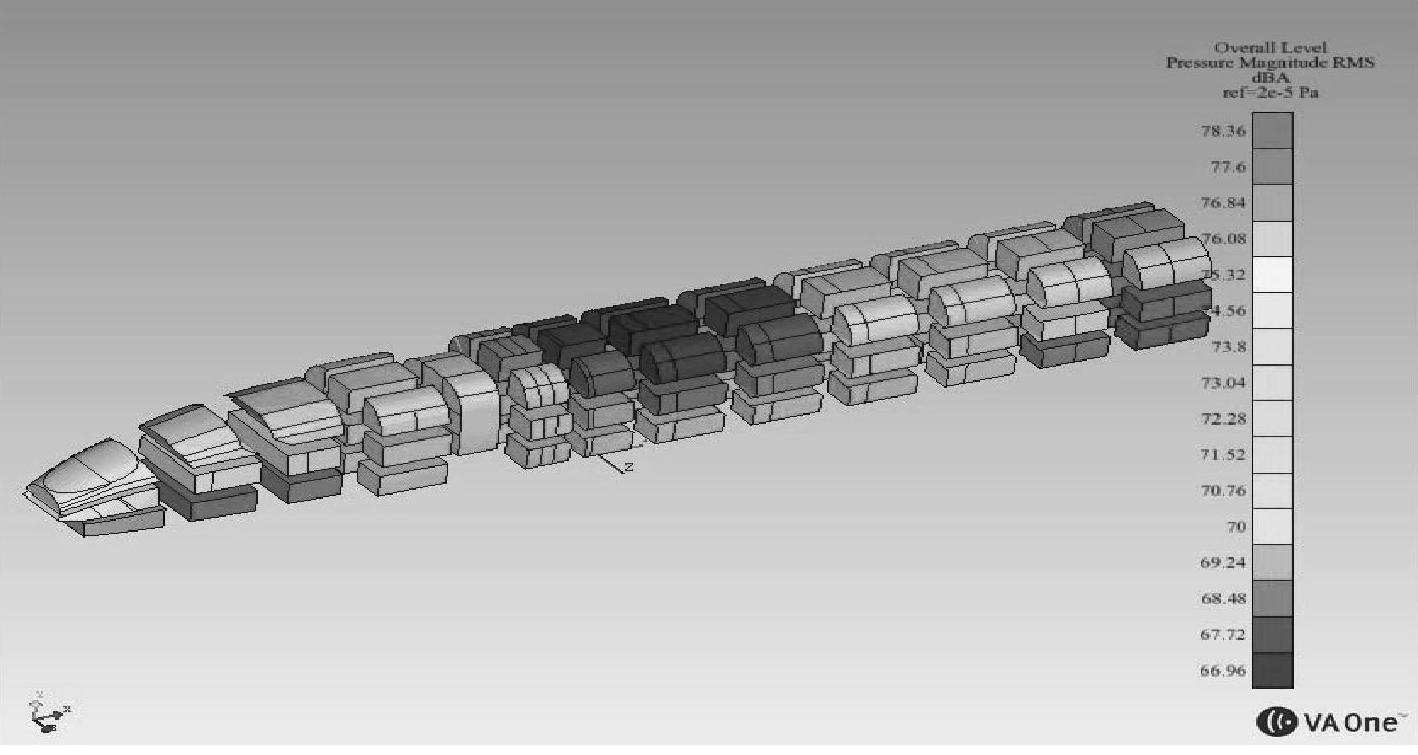
图5-148 车运行工况车内噪声

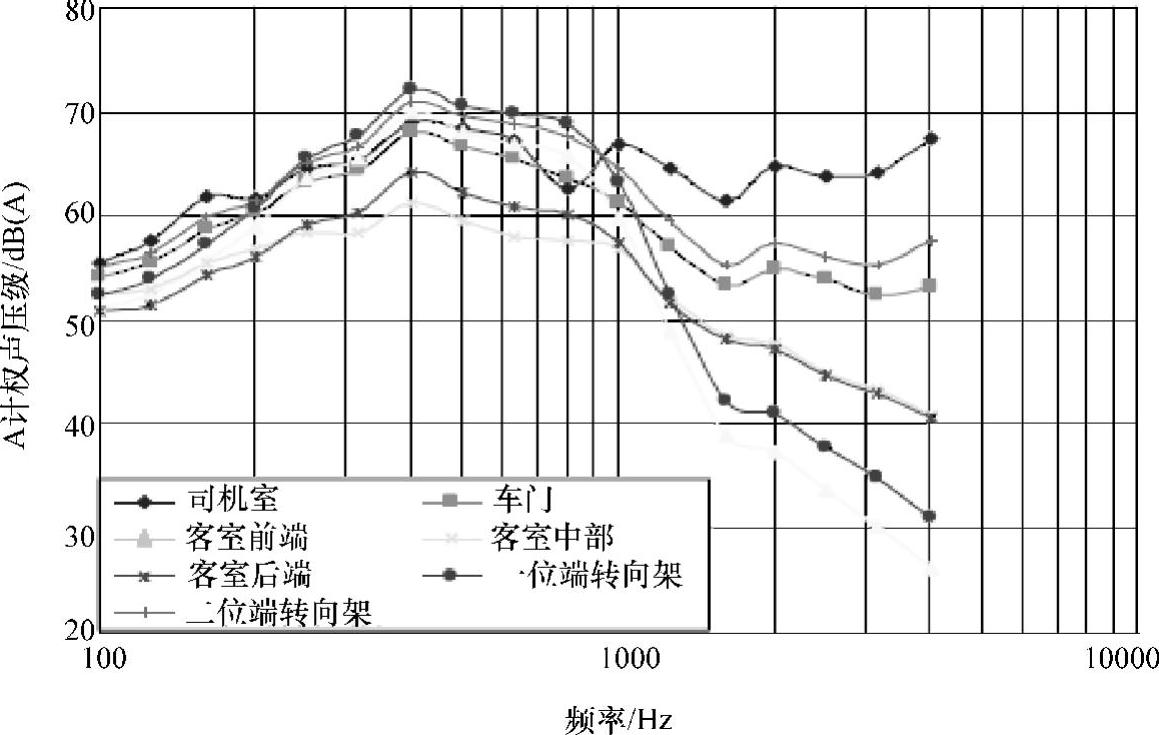
图5-149 车内地板1.5m处噪声值

RAYNOISE系统实质上也可以认为是一种音质可听化系统。它主要以几何声学为理论基础。几何声学假定声学环境中声波以声线的方式向四周传播。声线在与介质或界面（如墙壁）碰撞后能量会损失一部分，这样，在声场中不同位置声波的能量累积方式也有所不同。如果把一个声学环境当作线性系统，则只需知道该系统的脉冲响应就可由声源特性获得声学环境中任意位置的声学效果。因此，脉冲响应的获得是整个系统的关键。

以往多采用模拟方法，即利用缩尺模型来获得脉冲响应。20世纪80年代后期以来，随着计算机技术的高速发展，数字技术正逐渐占据主导地位。数字技术的核心就是利用多媒体计算机进行建模，并编程计算脉冲响应。该技术具有简便、快速以及精度可以不断改善的特点，这些是模拟技术所无法比拟的。计算脉冲响应有两种著名的方法：虚源法（Mirror Im-age Source Method，简称MISM）和声线跟踪法（Ray Tracing Method，简称RTM）。两种方法各有利弊。后来，又产生了一些将它们相结合的方法，如圆锥束法（Conical Beam Mehtod，简称CBM）和三棱锥束法（Triangular Beam Method，简称TBM）。RAYNOISE将这两种方法混合使用作为其计算声场脉冲响应的核心技术。

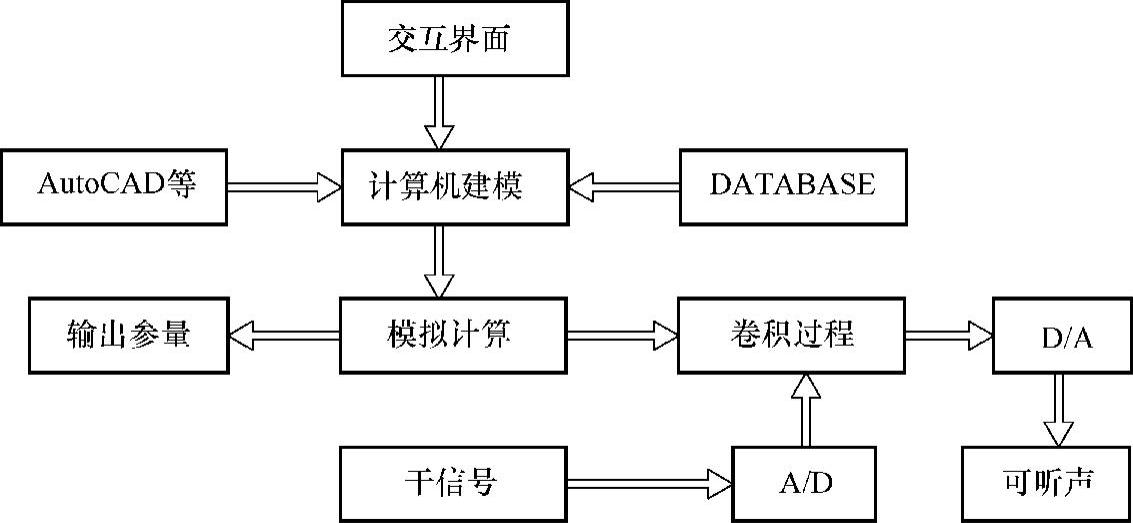
图5-150 RAYNOISE系统框图

（1）RAYNOISE系统计算机建模 RAYNOISE可以广泛用于工业噪声预测和控制、环境声学、建筑声学以及模拟现实系统的设计等领域，但设计者的初衷还是在房间声学，即主要用于厅堂音质的计算机模拟。进行厅堂音质设计，首先要求准确快速地建立厅堂的三维模型，因为它直接关系到计算机模拟的精度。RAYNOISE系统为计算机建模提供了交互界面。用户既可以直接输入由AutoCAD或HYPERMESH等产生的三维模型，也可以由用户选择系统模型库中的模型并完成模型的定义。

建模的主要步骤包括：

1）启动RAYNOISE。

2）选择模型。

3）输入几何尺寸。

4）定义各面的材料及性质（包括吸声系数等）。

5）定义声源特性。

6）定义接收场。

7）其他说明或定义，如所考虑的声线根数、反射级数等。

通过对计算结果进行处理，可以获得所关心的接收场中某点的声压级、A声级、回声图和频率脉冲响应函数等声学参量。如果还想知道该点的听音效果，可以先将脉冲响应转化为双耳传输函数，并将其与事先在消声室录制好的干信号相卷积，便可以通过双耳听到该点的听音效果。

（2）RAYNOISE软件的特点 RAYNOISE计算模型所采用的方法为综合了镜像声源法和声线跟踪法的混合方法，可在封闭空间、半封闭空间、开敞空间内进行众多声学参数的计算。该软件有如下特点：

1）计算模型表面数量无限制，因此可以尽可能详细、符合实际地仿真待预测声场的表面形状。

2）吸声材料的数量无限制，模型有多少表面就可定义多少种吸声材料。

3）数据库是开放式的，用户可随时根据实际情况对其修改，且可接受为文本文件格式的数据文件。

4）基于赛宾吸收的墙壁吸声仿真计算。

5）模型中声源的数量无限制，可以根据实际需要来设定足够数量的各种声源，并可在所定义的声源中任意选取所需数量的声源进行计算。

6）声像法中的反射阶数及声线法中的声线数皆可自定义。

7）内含各种CAD接口，如AUTOCAD、ANSYS、I—DEARS等。

8）友好的用户界面。

9）彩色图或等高线图输出。

10）计算结果包括：声压级、A声级、混响时间、混响半径、侧向反射率、早期反射声、清晰度（D50）、明晰度（C80）。在指定计算点后可得到该计算点的时间序列及对应的声线、该点的频率响应、该点的双耳脉冲响应及主观音质评价声音文件等。

根据CRH动车组车辆参数和既有线路区段条件，参考ISO 3095相关参数设置，分别对静置和运行状态下的车外噪声进行仿真计算，预测结果如图5-151、图5-152所示。

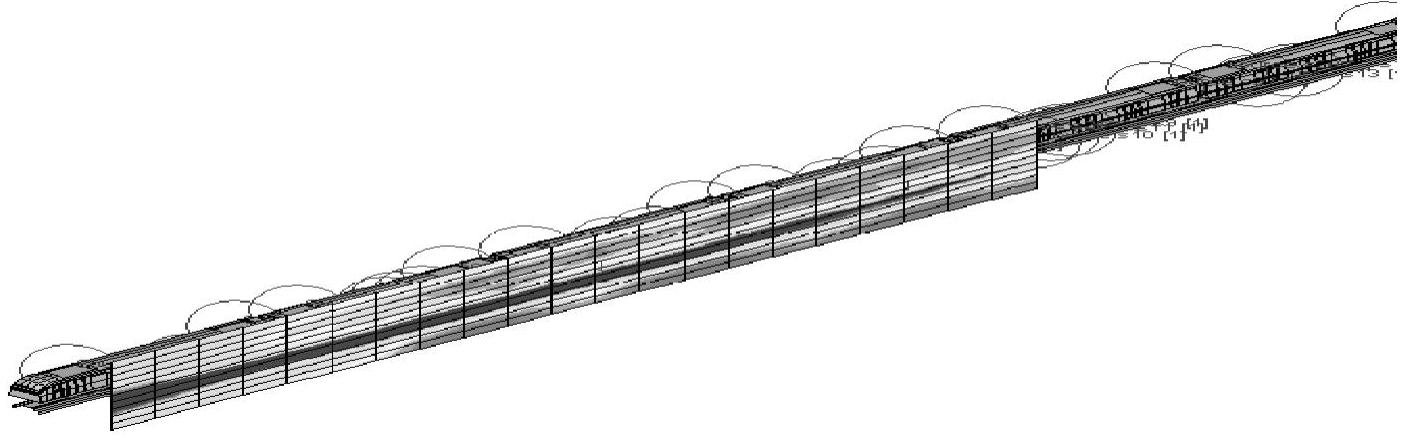
图5-151 车外远场25m预测结果

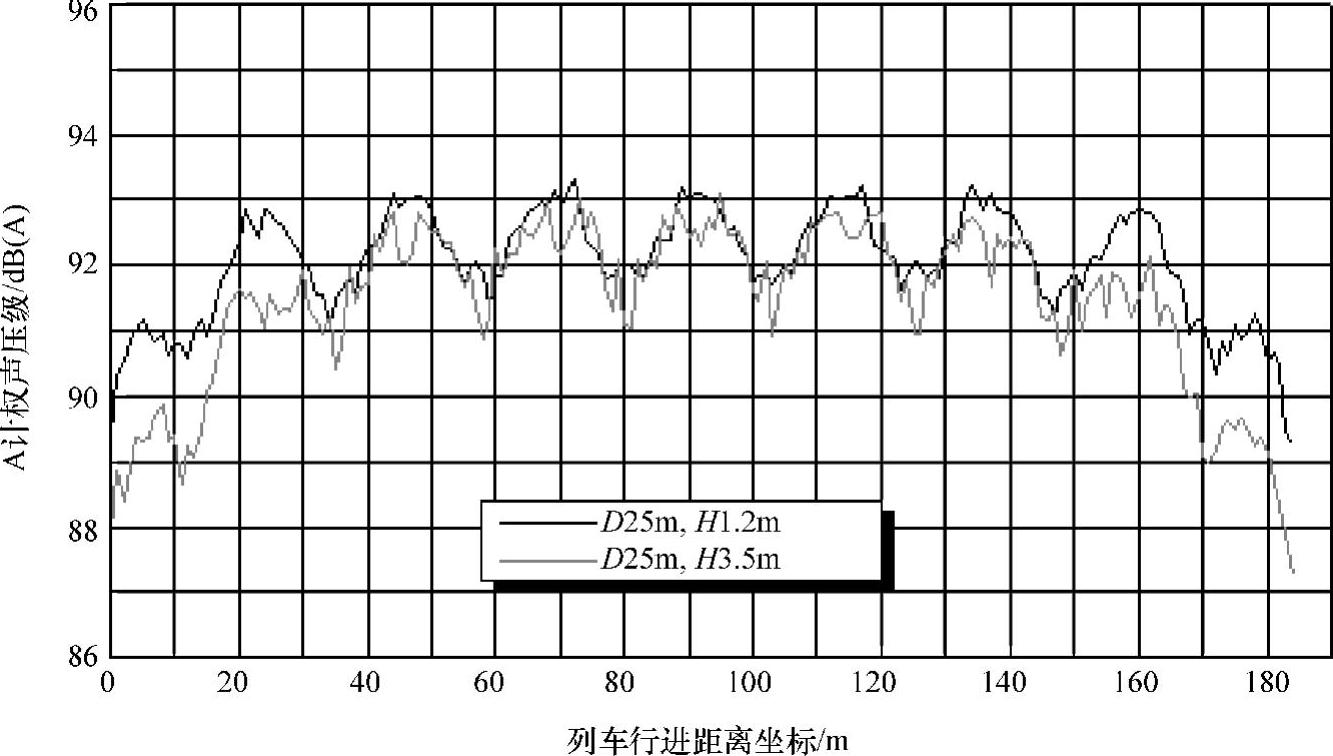
图5-152 车外运行噪声预测结果（速度：300km/h）