动车组噪声控制技术：基于试验的隔声量仿真模型修正

5.3.1.1 隔声仿真计算的应用方法

对中空铝型材的分析方法有很多，包括有限元法、统计能量法、FE-SEA混合法、等效法等，下面进行介绍。

（1）有限元法 结构-声耦合有限元理论计算结构隔声的形式为

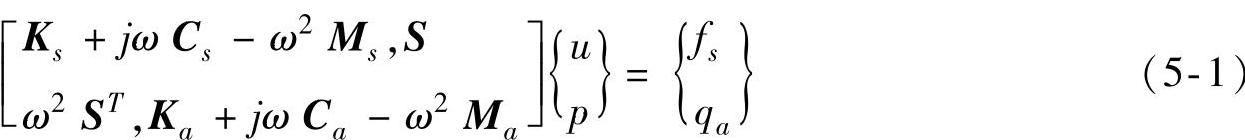
式中，K，C，M分别表示刚度矩阵、阻尼矩阵和质量矩阵，下标s、a分别表示结构和声腔。S为结构网格和声腔网格耦合因子矩阵，u、p分别表示节点位移和结点声压，f_s、q_a分别表示外界力和声源源强。假设铝型材镶嵌在无限大障板中，板两侧是空气。在板的一侧有一个随机入射白噪声声源，声源一侧声压处处相等，相位无规。板的另一侧是半无限大自由声场，如图5-96所示。

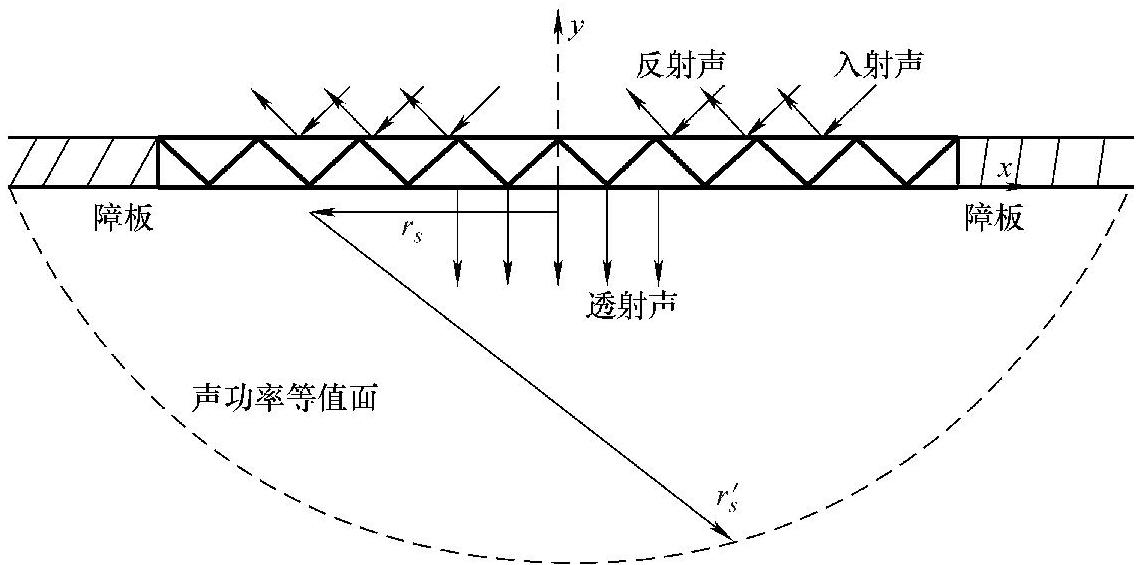
图5-96 铝型材隔声计算模型

在此假设下，式（5-1）简化为

式中Z_S=K_s+jωC_s-ω²M_s，Z_A=K_a+jωC_a-ω²M_α，由此可以计算节点位移和结点声压：

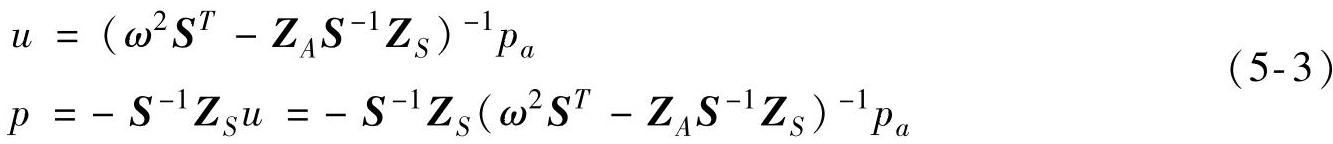
板的振动在半无限大空间辐射声功率，大小等于板表面声功率：

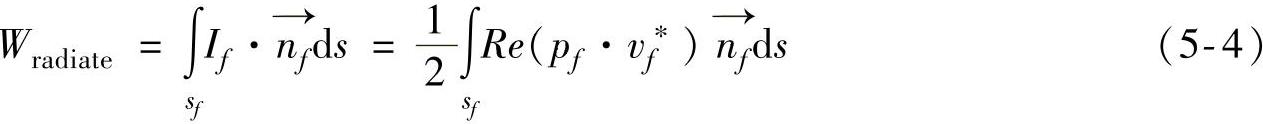
根据上式可以计算出隔声量大小为

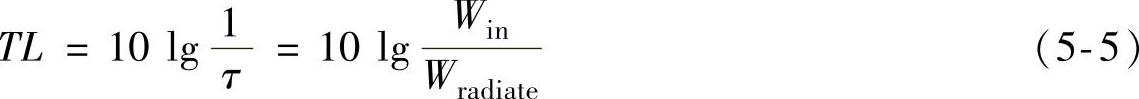
（2）FE-SEA混合法 有限元（FE）方法求解隔声量时，在中低频有很大的优势，结果较准确，但随着频率的提高，有限元法对网格的要求也随之提高，导致计算时间过长。而统计能量法（SEA）可以有效地求解高频问题，解决计算时间长的缺陷，因此衍生出FE-SEA的混合建模法。下面对FE-SEA混合法进行详细介绍。

类似于SEA，一个混合系统可以划分为若干子系统，每个子系统都有形状区域和边界，区域可能是封闭的也可能是开孔的或者内部不连续的，而子系统之间边界可能接触也可能不接触，因而会有各种边界形式。大体来说，子系统边界可以划分为确定性边界和随机边界两大类，如图5-97所示。

其中确定性边界指其性质能够被辨认的边界，比如子系统之间互相接触的边界都是确定性边界，其特点是能量可以从边界传递进来或出去。其他边界属于不确定性的，称为随机边界。

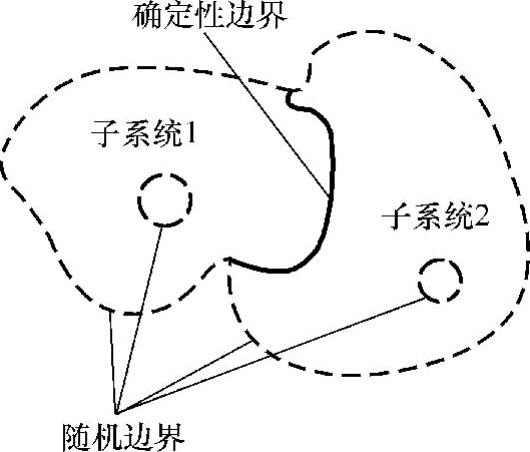
图5-97 子系统边界示意图

假设一个系统被划分为若干子系统，在分析频带内某些子系统尺寸比弯曲波长大很多，模态数和模态密度足够大，可以定义为SEA子系统；另一些子系统尺寸和弯曲波相当，模态数较低，则可以定义为FE子系统。SEA子系统和FE子系统通过确定性边界连接，如图5-98所示。

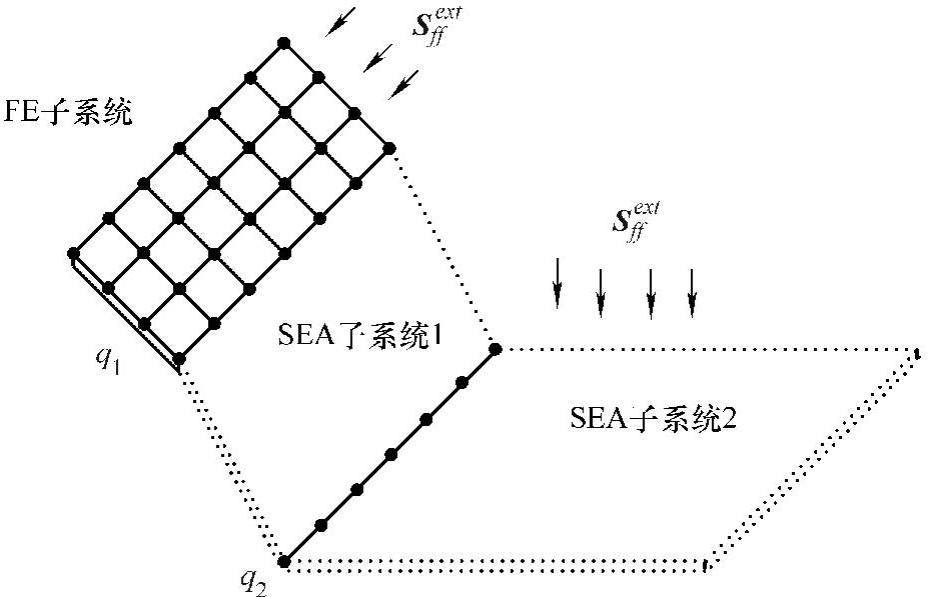
图5-98 FE-SEA子系统划分示意图

图中q₁表示有限元子系统的位移向量，该向量既包含内部节点位移向量也包含与其他子系统接触边界的节点位移向量，q₂表示SEA子系统之间连接处的位移向量（线接触可以用若干离散点表示）。那么向量q=[q₁^T，q₂^T]^T则完全表征了系统FE结构位移和所有连接边界的位移。

假设FE子系统的动态刚度矩阵为D_d（ω），那么其运动方程为

D_dq=f_d （5-6）

式中f_d是作用在自由度的广义力。

对于SEA子系统而言，由于波传播的统计平均特性，可将子系统波动场分离为直达场和混响场，类似于房间声学直达声场和混响声场的概念。直达场描述的是在忽略随机边界情况下，和确定性边界位移联系在一起的自由波动位移场；而混响场描述的是在直达场中加入随机边界或者边界条件为受挡边界条件（位移为0）的确定性边界后新出现的反射位移场，如图5-99所示。由此得第j个SEA子系统非耦合运动方程：

D^（j）_dirq=f+f^（j）_rev （5-7）

式中D^（j）_dir为第j个SEA子系统的直达场动态刚度矩阵，f为广义力向量，f^（j）_rev为反射边界的受挡反射力。

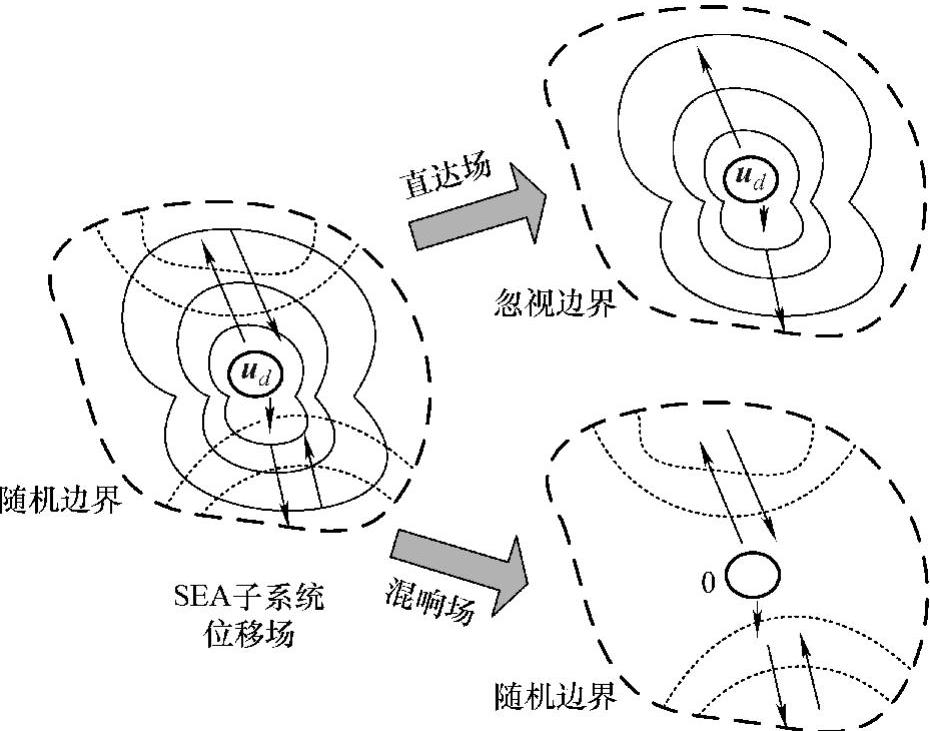
图5-99 SEA子系统位移场分解示意图

将FE子系统运动方程式（5-6）和所有SEA子系统运动方程式（5-7）联立可得系统运动方程：

式中f_ext为系统外部激励广义力向量，总动态刚度矩阵D_tot表示为

如果SEA子系统存在随机边界，那么式（5-8）中的反射力就变成随机变量，因此可以将式（5-8）写成互谱的形式，并将所有随机边界通过总体平均得到：

〈S_qq〉=D^-1_tot〈S_ff〉D^-H_tot （5-10）

〈〉表示总体平均，平均力互谱的具体形式为

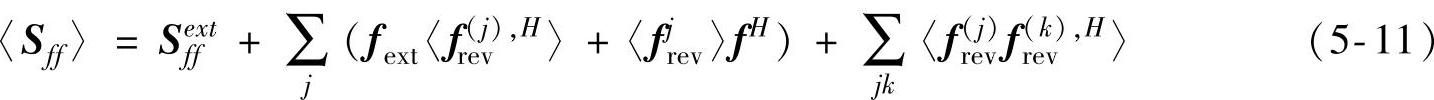
上标H表示哈密顿转置，有研究表明，由于随机边界的不确定性，受挡反射力的统计平均特性满足以下关系：

〈f_rev〉=0；S^rev_ff=〈f_revf^H_rev〉=αIm{D_dir} （5-12）

α是和反射场幅值有关的常量，第j个SEA子系统的α_j的表达式为

式中E_j是子系统j混响场总能量，n_j是对应模态密度。因而式（5-11）变成：

将式（5-12）～式（5-14）代入式（5-10）得

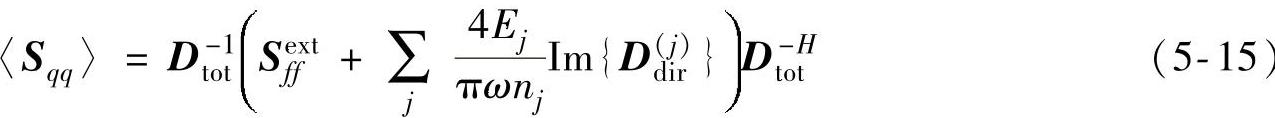
上式就是系统的位移响应方程，其能量和模态密度比需要通过下文的能量平衡方程得到。

系统受到外部激励时每个子系统都会产生相应的输入功率和输出功率，输入功率为

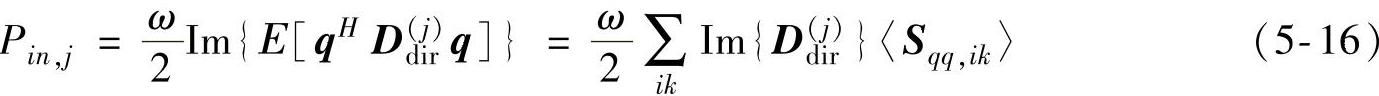
将式（5-15）代入式（5-16）得到：

式中

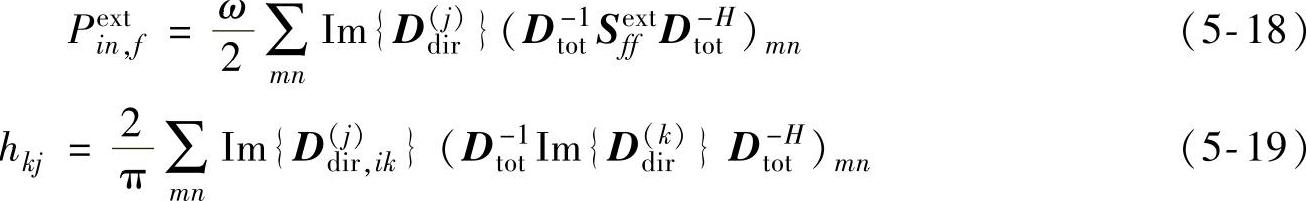
式中h_kj定义为功率传递系数，表示的是单位模态密度能量从子系统k输入到子系统j的比例。由SEA耦合损耗因子η_kj的定义可知h_kj和η_kj的关系：

h_kj=ωn_kη_kj （5-20）

由式（5-17）可知，SEA子系统输入功率包含了外部激励和所有子系统混响场反射能量的贡献。式（5-19）中动态刚度矩阵是对称矩阵，因而有h_kj=h_jk。

子系统的输出功率包含自身耗散功率和通过边界流向接触子系统的功率，表示为

P_out，j=P_diss，j+P_rev，j （5-21）

式中

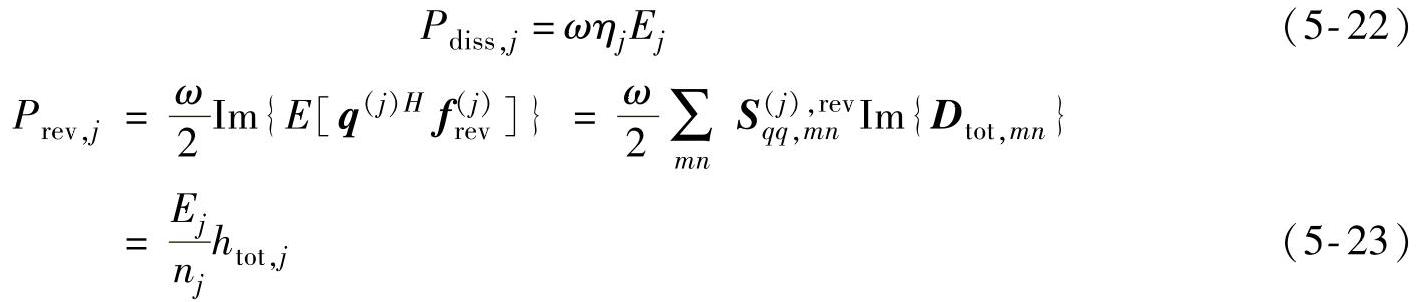
式中S^{（j），rev}_qq表示子系统混响场激励产生的响应，总功率传递系数h_tot，j表示为

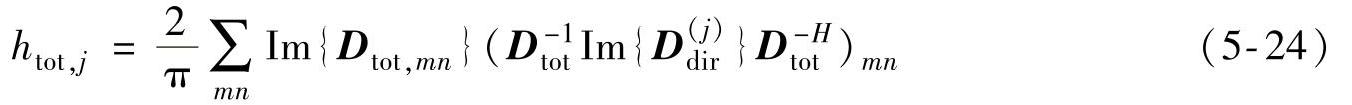
总动态刚度矩阵可以展开成：

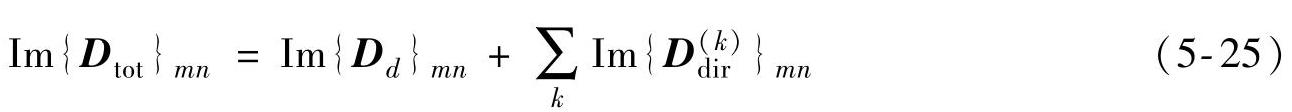
因而将式（5-24）、式（5-25）代入式（5-23）可得：

式中h_d，j表示SEA子系统j的单位模态密度能量传递到FE子系统中并被该子系统耗散的能量传递系数，表达式为

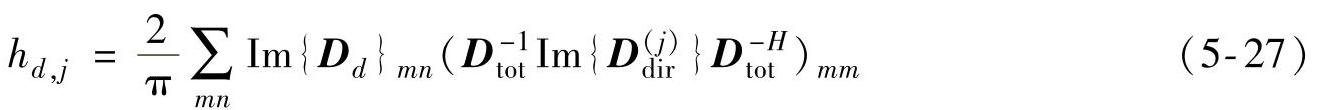
由能量平衡关系可知，子系统稳定后输入功率和输出功率应相等P_in，j=P_out，j，最终得到Hybrid-SEA的能量平衡方程：

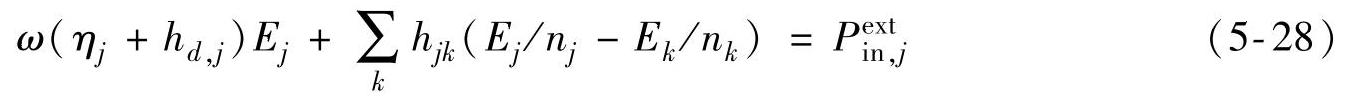
式（5-28）和式（5-15）组成了整个系统的完整求解方程。从式（5-28）可以看出，如果FE子系统是无阻尼的，或者系统中不存在FE子系统，那么h_d，j为0，上式就变成纯粹的SEA能量平衡方程；如果整个系统没有SEA子系统，那么式（5-28）就不存在，只剩下式（5-15）的FE运动方程，成为纯粹的FE求解问题。因而Hybrid-SEA方法既可以解决纯SEA或纯FE问题，也可以解决FE-SEA混合求解问题。

（3）等效模型参数 铝型材等效为均质三明治板结构，表面板仍为铝单板结构，中间层等效为各向异性介质，如图5-100所示。

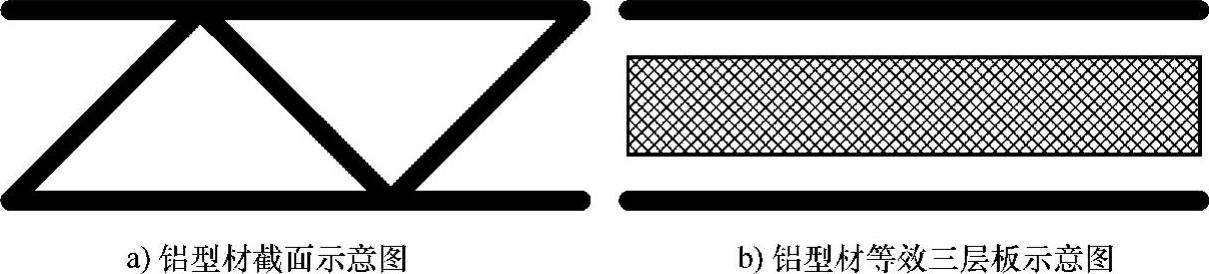
图5-100 铝型材结构等效示意图

波纹芯层等效为均匀介质，主要是对模量、泊松比、密度进行等效。波纹板尺寸参数如图5-101所示，已有研究表明等效参数可表示为式（5-29）～式（5-40）的形式。

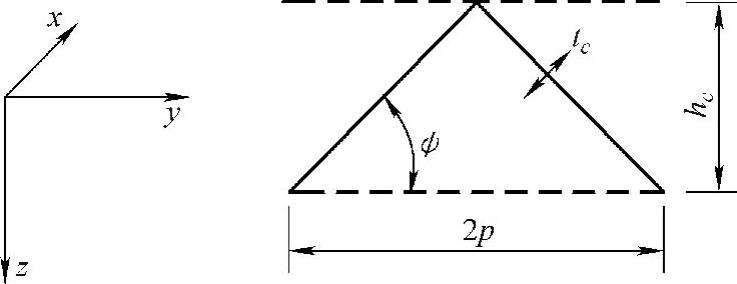
图5-101 中间层波纹板几何参数

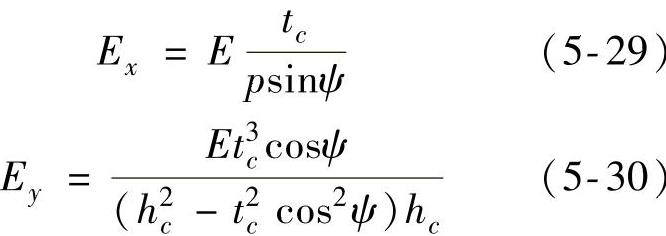
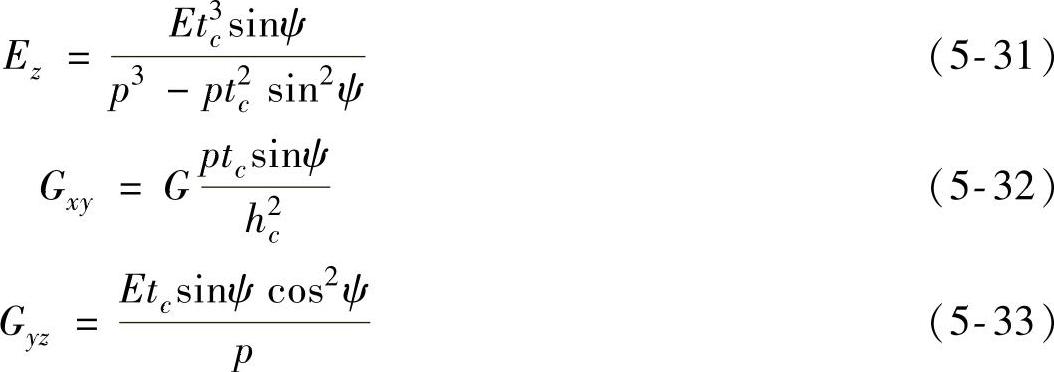
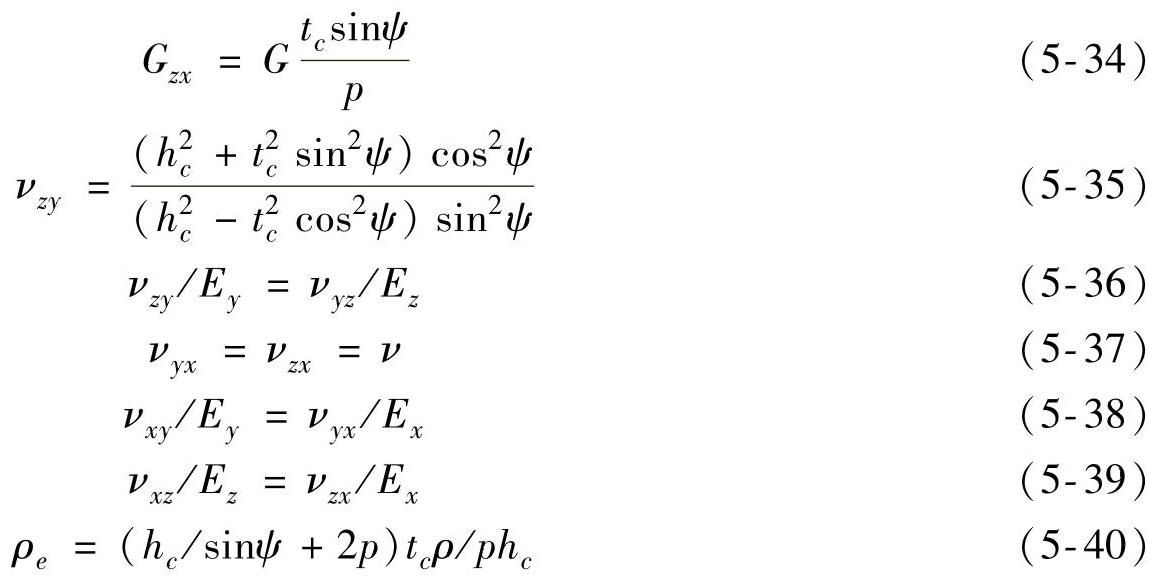
以上公式中E、G、ν、ρ分别表示波纹板铝材料的杨氏模量、剪切模量、泊松比和密度。

5.3.1.2 铝型材模态测试(www.xing528.com)

基于铝型材模态测试结果修正有限元板件模型的边界约束条件，保证前10阶模态及振型控制在5%误差范围内。

样件模态测试环境放置于混响室洞口，四周密封状态与隔声测试条件一致。

（1）基本理论 实验模态分析的基本流程如图5-102所示。

图5-102 实验模态分析流程图

目前已有比较成熟的理论识别模态参数，这里做一简要介绍。

在外界激励下多自由度系统的频域运动方程为

（-ω²M+jωC+K）X（ω）=F（ω） （5-41）

根据传递函数的定义，

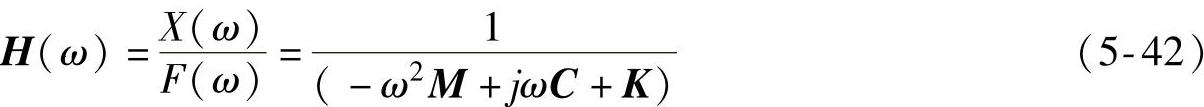
它是N×N的矩阵，矩阵内元素H_ij表示响应点x_i对激励点f_j的传递函数。在系统的比例阻尼假定下，根据正则振型的正交性，刚度、质量、阻尼矩阵可以写成以下形式：

因此得传递函数矩阵的叠加组合形式：

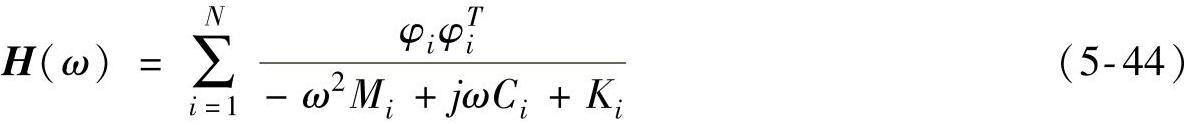
上式中φ是振型基向量，M_i，K_i，C_i分别为第i阶模态质量、模态刚度、模态阻尼。假设模态质量是归一化质量，则其第i阶模态质量、模态刚度、模态阻尼转化成：

式中ω_i为无阻尼模态频率，ζ_i为模态阻尼比，则式（5-44）的传递矩阵中内部单元H_re（ω）可以改写为

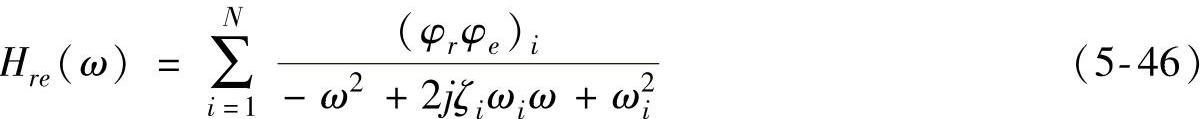
这里无阻尼模态频率ω_i与测试得到的传递函数第i阶共振频率的关系是

从式（5-46）可知，传递函数矩阵每个元素包含了-ω²+2jζ_iω_iω+ω²_i，只有φ_i是可变的，因此为了求出该模态基矢量，只需要测出传递函数矩阵的一行或一列即可。假设某被测对象整个区域被划分为n个测点，则理论上可以产生n×n的传递矩阵，但是测试时只需要测试n个传递函数。

因此，实验模态分析的主要步骤如下：

1）测试完整的一组激励信号（e）和响应信号（r）集合，将信号分组、加窗、滤波。

2）采用FFT变换和谱密度方法计算传递函数：H_er=S_er/S_ee。

3）计算相干函数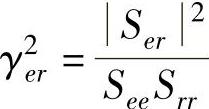：，挑选出相干系数γ_er接近1的传递函数（该步骤也可以在测试时直接观察选择）。

4）将传递函数采用曲线拟合的方法写成这种形式：

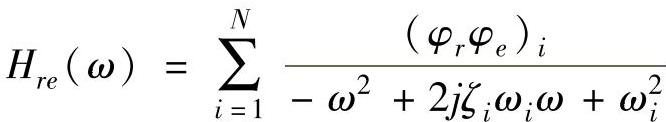，则可以提取出振型向量φ_i（即留数（φ_rφ_e）_i）、无阻尼固有频率ω_i和模态阻尼比ζ_i。

5）形成模态振型基矩阵φ=[φ₁，…，φ_n]，计算φ^-1。

6）获取模态质量矩阵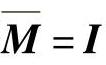，模态刚度矩阵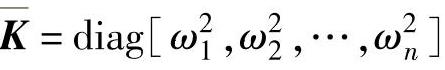，模态阻尼矩阵。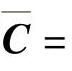

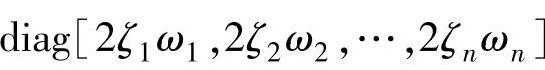7）最后计算系统质量矩阵、刚度矩阵、阻尼矩阵：

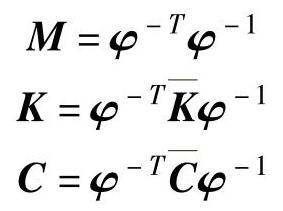
（2）实验模型 对铝型材的模态实验采用力锤测试法，为了降低加速度计质量的影响，使用固定加速度、移动力锤法进行测量。

中空铝型材安装在隔声窗内，内部无法布置加速度计，因此对发射室与接受室的两个板面进行加速度的布置，两板面的测点网格布置如图5-103所示。

图5-103 板面测点网格图

将整个板面分为6行8列的48个小块，每小块的尺寸为0.15625m×0.185m。加速度布置于第20小块区域，使用力锤从第1小块激励，按编号顺序激励直到完成对48个小块的激励，获得48个传递函数。

测试采集仪使用Pulse3160，实验结束后获得两个Pulse文件Modal_hammer_Bowenban_sender与Modal_hammer_Bowenban_receiver，分别包含2个板面的48个传递函数，对其进行后处理即可获得2个板面的模态频率。

（3）实验结果 对实验数据进行处理，获得中空铝型材两块板面的传递函数。其中发射室板面传递函数，如图5-104所示，接收室板面传递函数如图5-105所示。

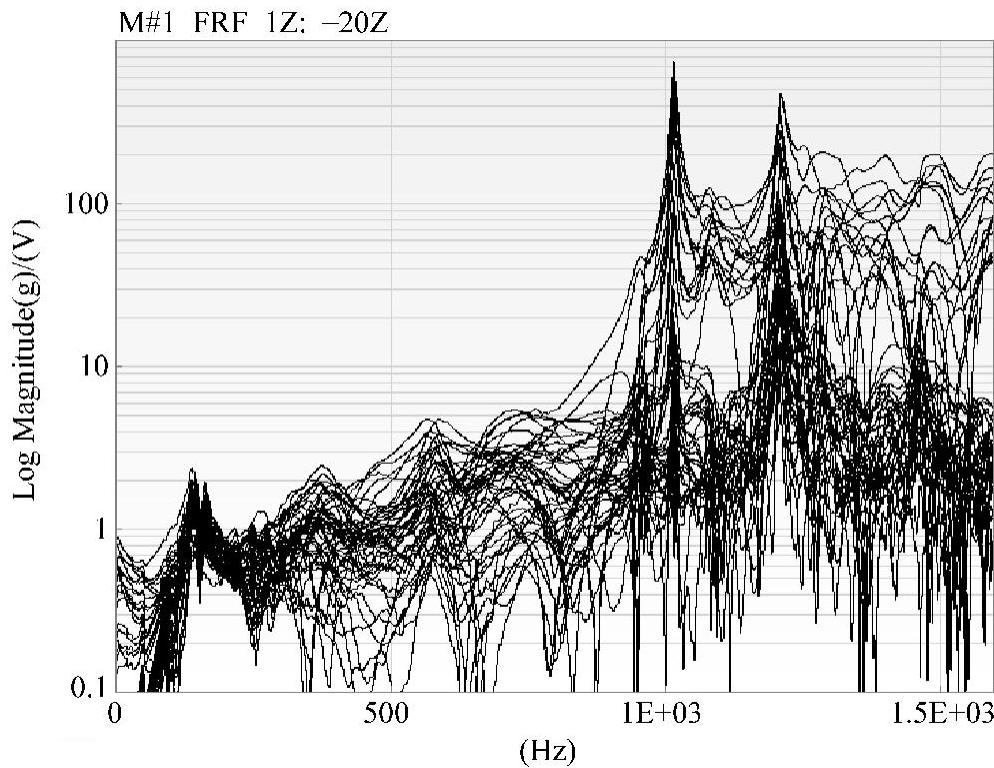
图5-104 发射室板面的48个传递函数

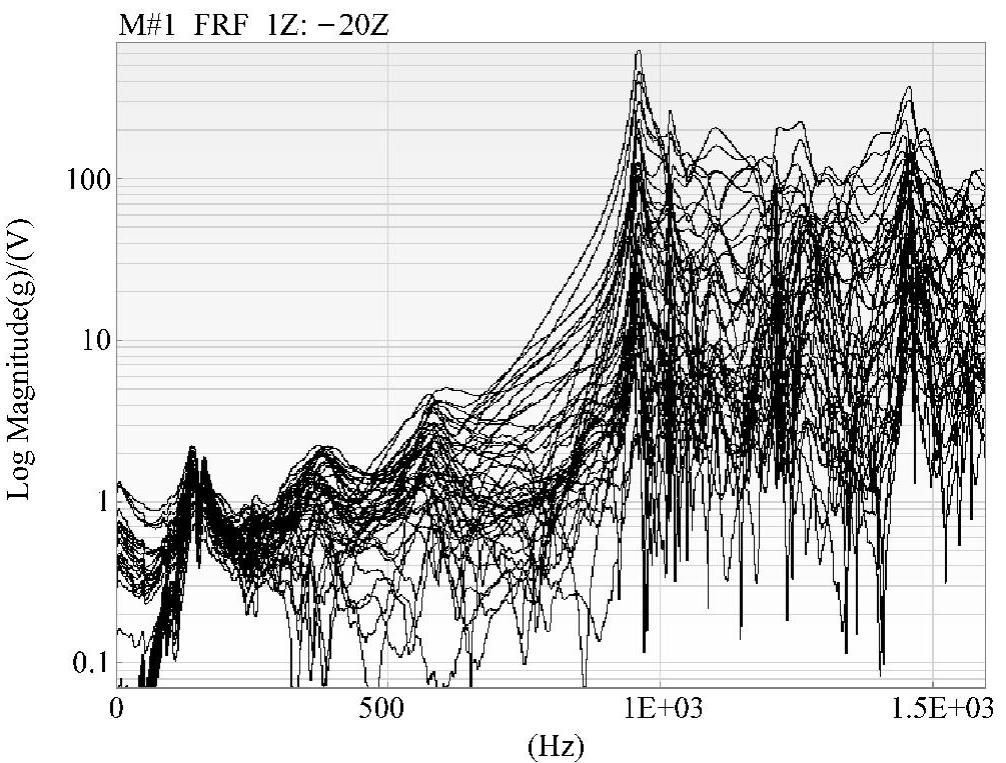
图5-105 接收室板面的48个传递函数

对上述传递函数进行模态识别，获取两块板面的模态频率与模态振型。两块板面的模态频率结果见表5-12，相应的模态振型如图5-106、图5-107所示。

表5-12 中空铝型材两板面模态频率结果

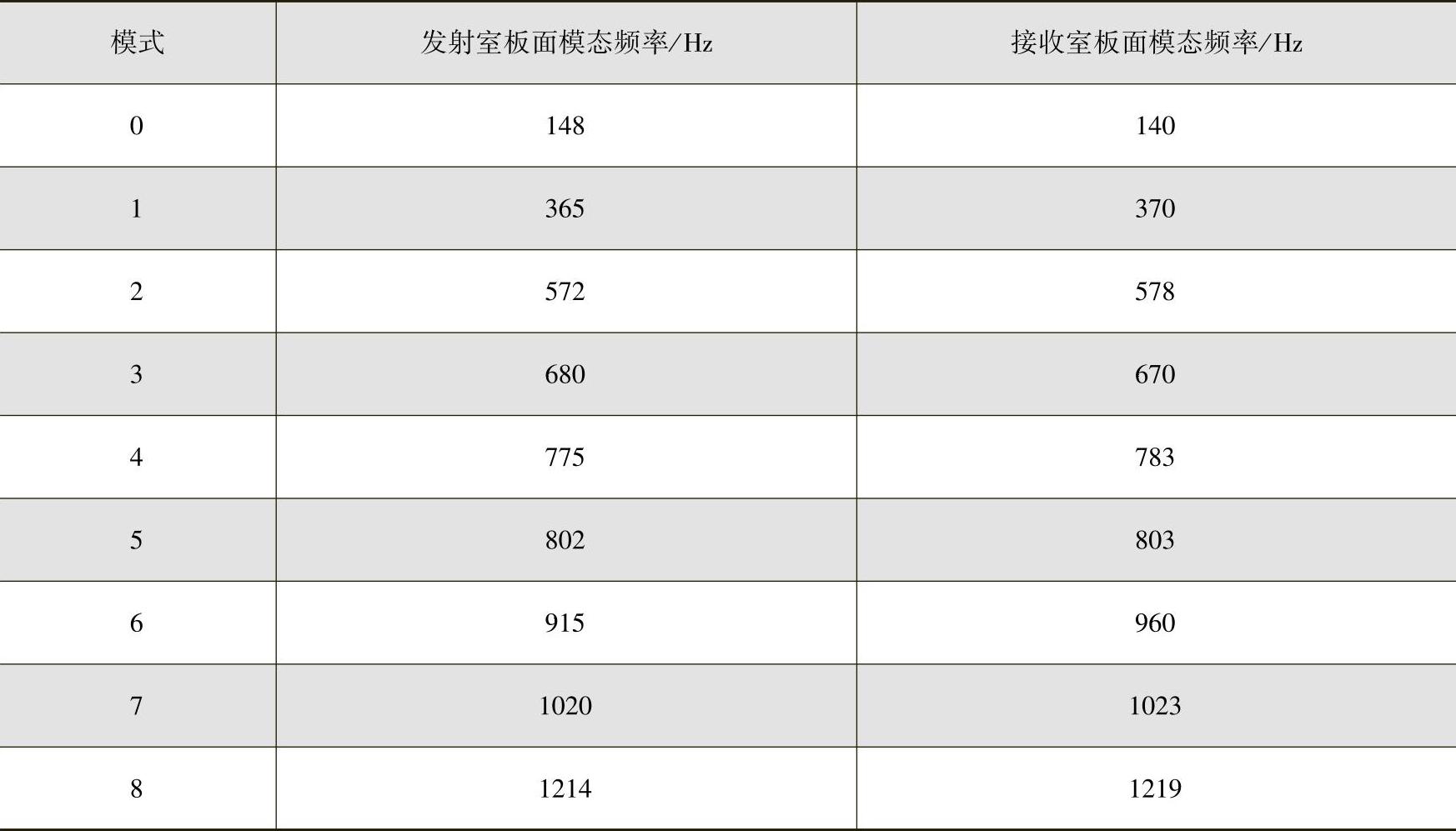
两块测试的板面都属于中空铝型材，因此它们的模态频率结果就是中空铝型材的模态频率结果，综合两板面的模态频率结果，得到中空铝型材的模态结果见表5-13。

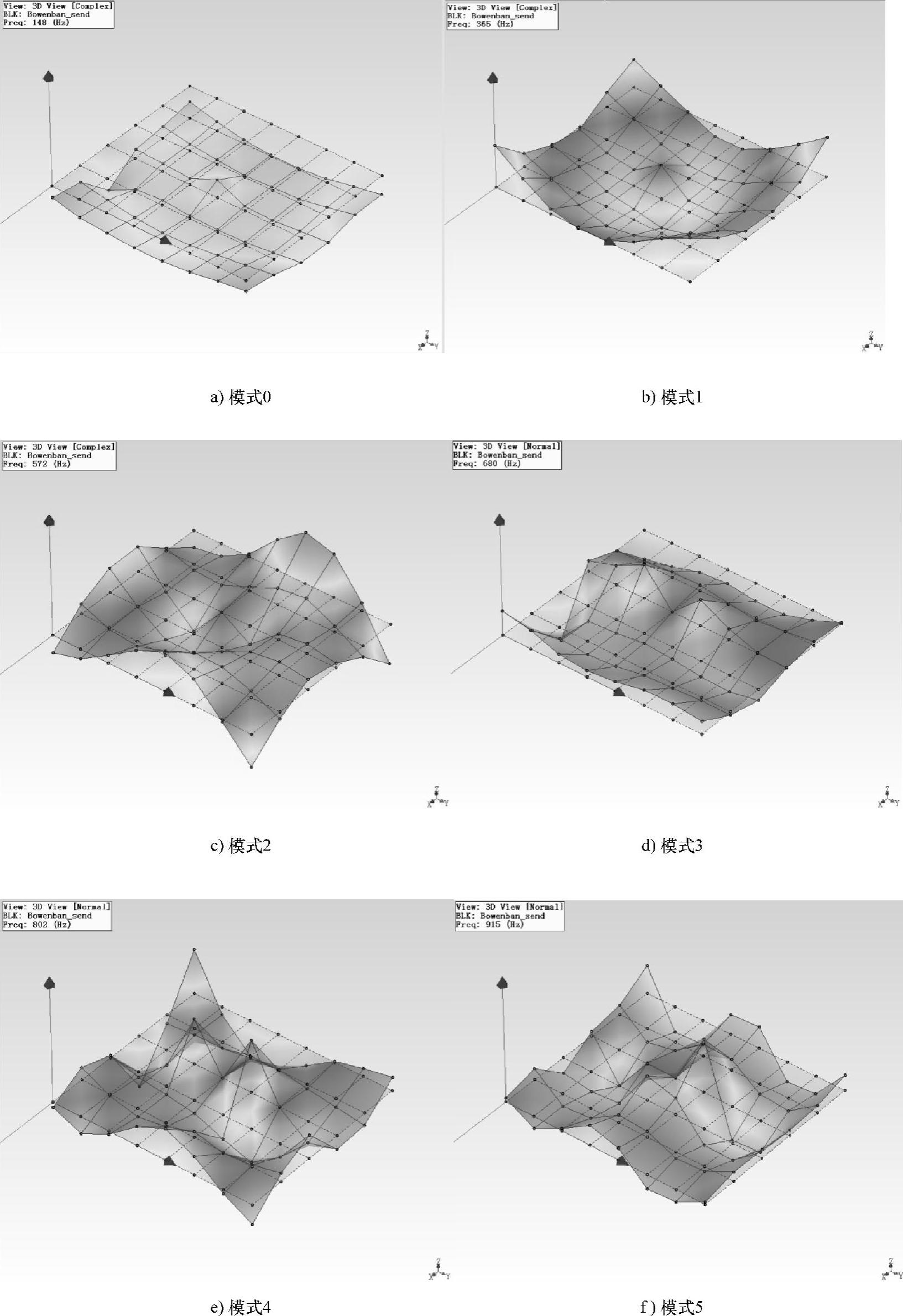
图5-106 发射室板面的模态振型

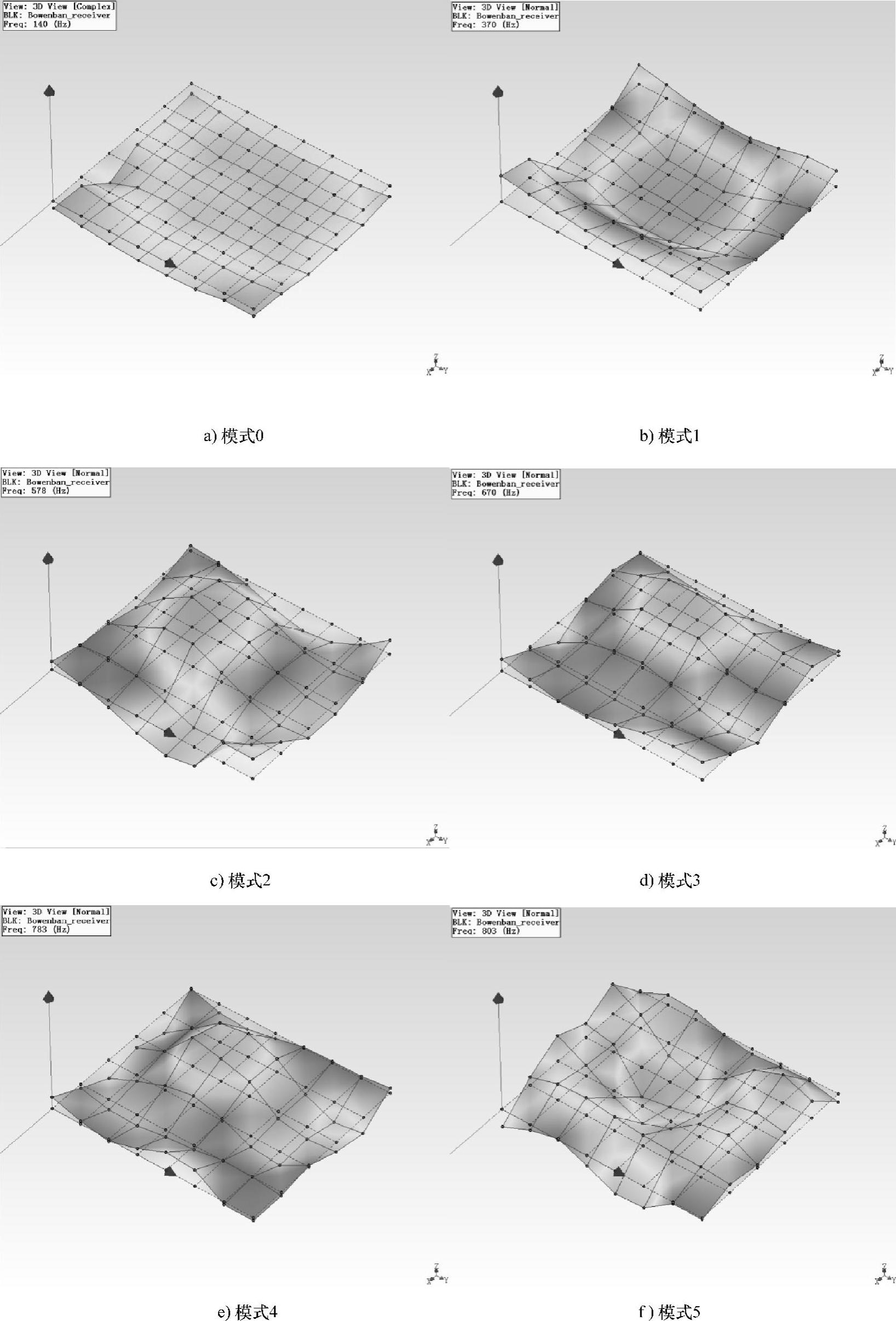
图5-107 接收室板面的模态振型

表5-13 中空铝型材模态频率结果

5.3.1.3 铝型材损耗因子测试

本实验采用脉冲法获取铝型材的损耗因子。当铝型材受到脉冲激励时，会产生随时间迅速衰减的振动信号，该衰减信号是铝型材自身损耗和边界条件损耗的综合作用结果。单位激励加速度响应信号可以表示为

式中η_t是损耗因子，其值为单位圆频率输入功率P_in，k和受激子系统的能量E_k之比：

由于损耗因子η_t一般和频率有关，在宽频带范围，没有必要得到每个频率的损耗因子。宽频带分析振动和噪声一般采用1/3倍频程频域，因而可以只计算1/3倍频程中心频率处的η_t。假设响应信号经过中心频率为ω_n，带宽为ω_d的带通滤波器滤波后，响应信号变为

式中A是幅值，η_s是带宽内的损耗因子。对信号滤波可以采用巴特沃斯带通滤波器，选择合适的阶数可以获得较好的结果。

将中空铝型材放置于隔声窗口内，安装好之后，采用力锤激励法进行激励，拾取板件上某些测点的加速度信号，对得到的数据进行处理，即可得到中空铝型材的单位激励加速度响应信号。

进一步通过Hilbert变换求响应信号包络，进而计算中心频率处的损耗因子η_s。滤波后信号a_n（t）的Hilbert变换表示为

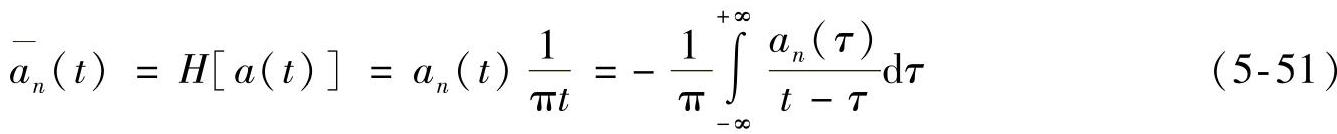
响应信号的解析信号为

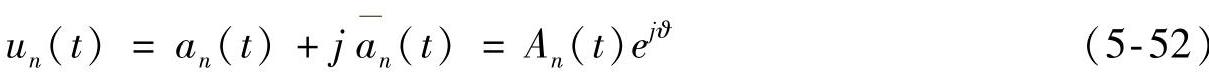
解析信号的幅值A_n（t）就是响应信号的包络，表示为

将包络取对数得到衰减曲线，由衰减曲线可识别出对数衰减率δ，进而得到损耗因子η_s：

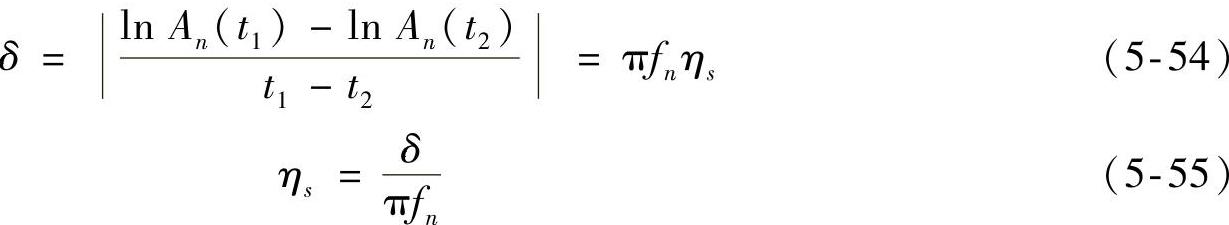
计算1/3倍频程630Hz的损耗因子的过程如图5-108所示，其中滤波信号的对数包络经常出现衰减快和衰减慢的斜率。有研究指出衰减率应取衰减较快的初始斜率1作为对数衰减率，这里直接通过观察原始信号迅速衰减的时间段选取衰减快的斜率进行计算。

通过对实验数据的处理，最终获得铝型材的损耗因子结果，见表5-14。

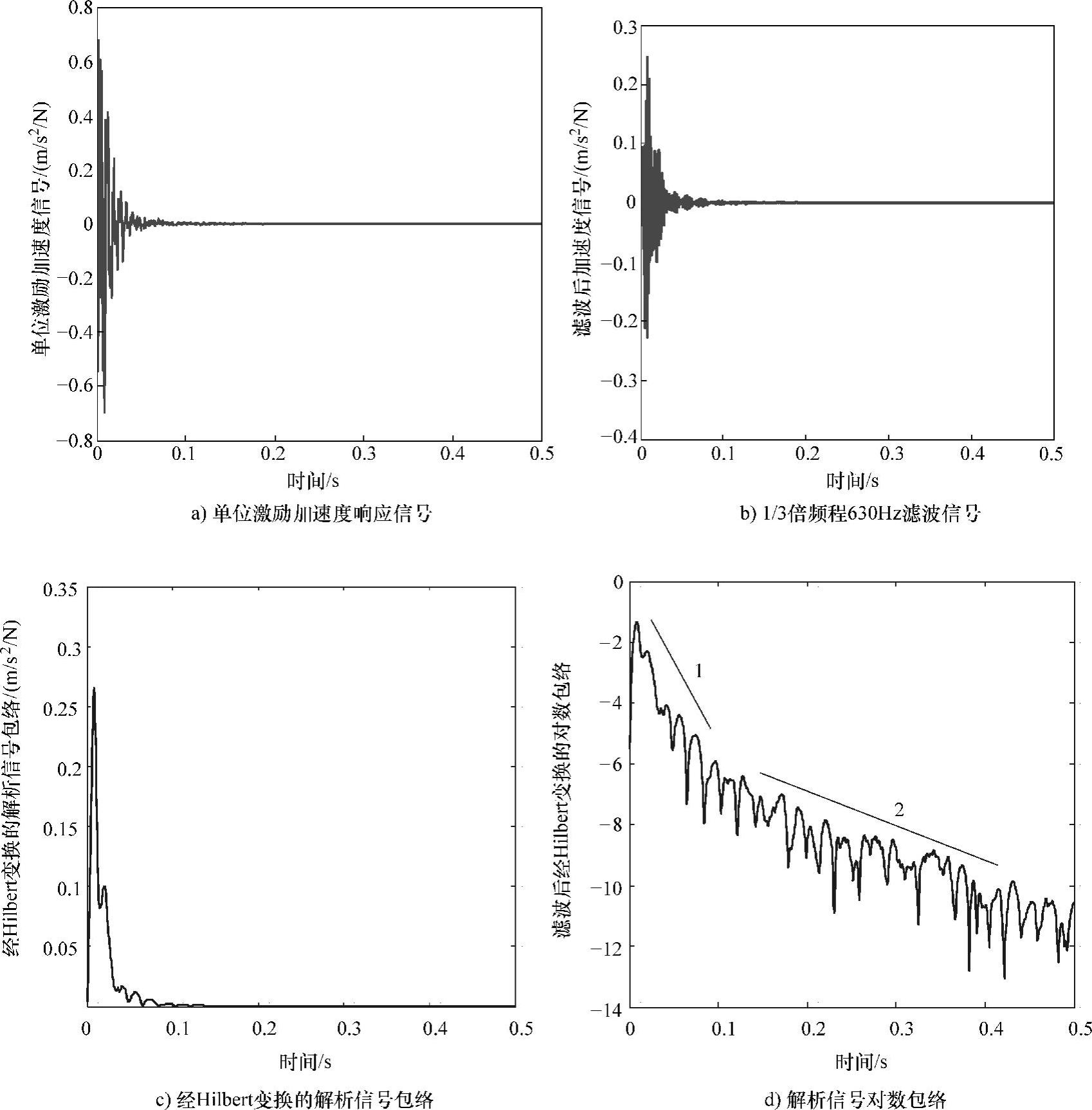
图5-108 响应信号求对数包络衰减率过程

表5-14 铝型材的损耗因子

5.3.1.4 隔声量计算

低频区100～250Hz选取等效方法，315～1250Hz基于有限元法（阻尼）并施加约束控制前几阶模态与测试接近；1600～4000Hz高频区域选取SEA方法的结果，得到综合的仿真值见表5-15，最终的隔声量曲线对比结果如图5-109、图5-110所示。

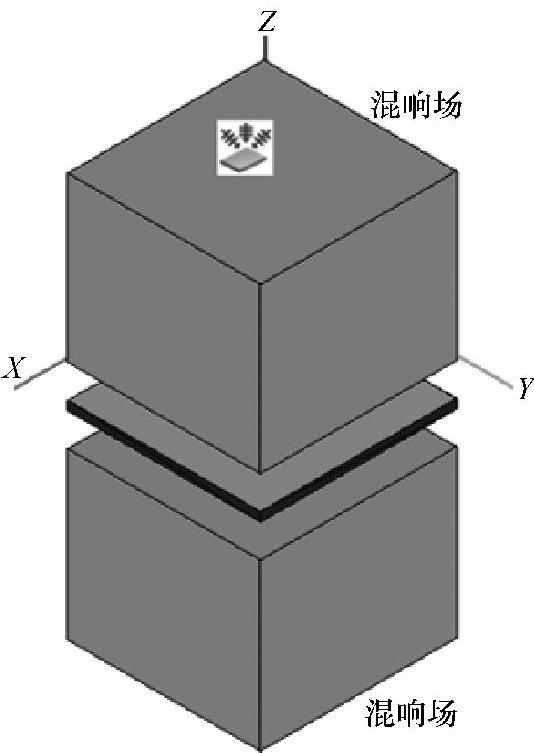
图5-109 隔声量计算模型

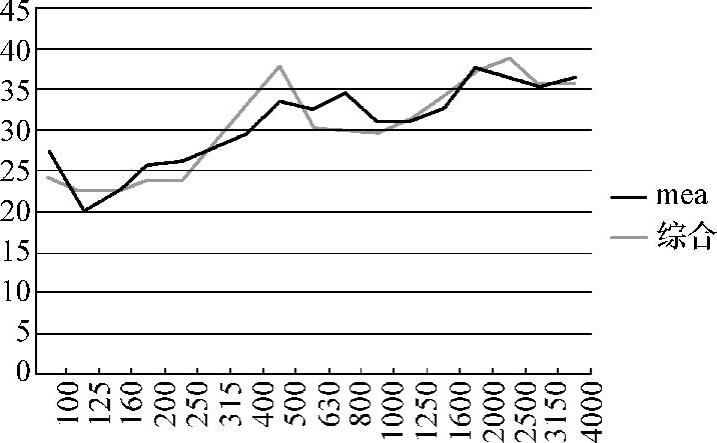
图5-110 试验仿真隔声量对比

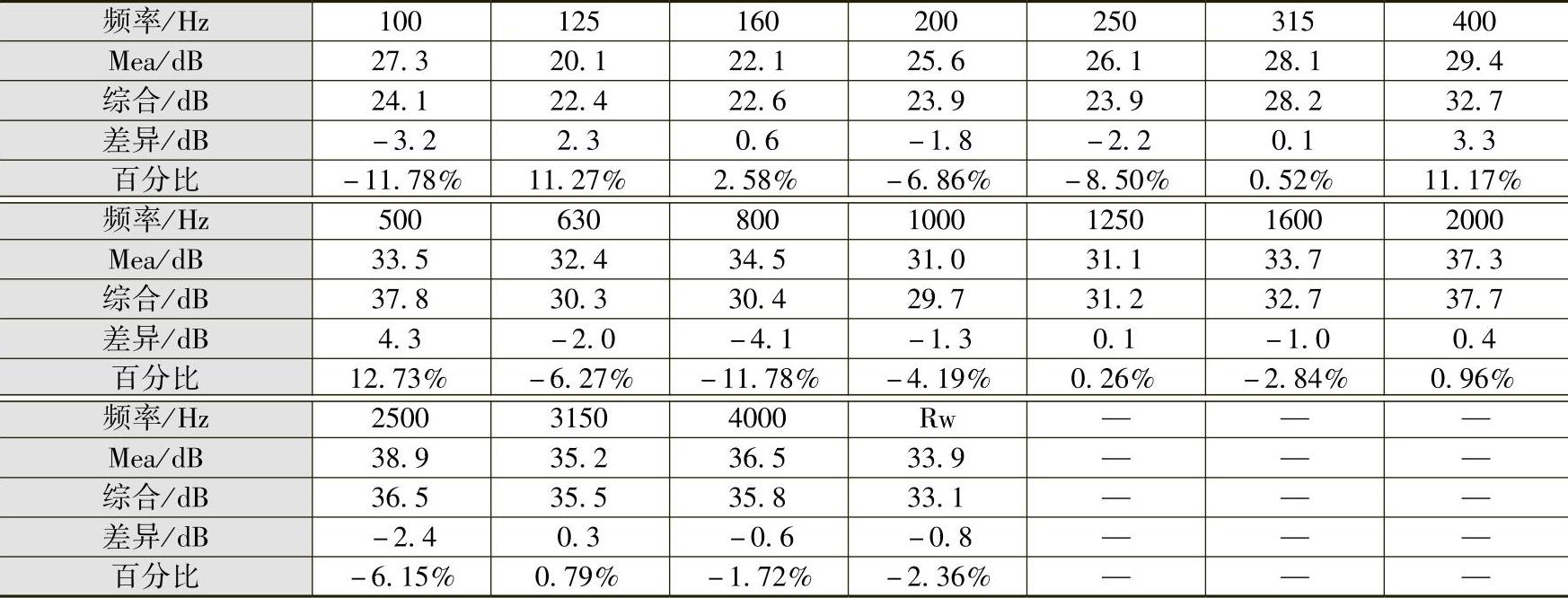
表5-15 综合结果与实验结果的比较