动车组气流声源分类及噪声控制技术

在气流（或水流）中声源有三类：单极子、偶极子、四极子。

（1）单极声源的辐射 单极声源简称单极源或点源，如一个周期的小幅度膨胀收缩的球体——脉动球，向四周空间均匀地辐射球面波，就把这个脉动球看成一个单极声源。

当脉动球以正弦形式脉动时，距球心为r处的声压为

式中 Q——单源强度，是脉动球面处的空气体积流的最大值，Q=πD²v；

D——脉动球直径；

v——脉动球表面振动速度幅值；

ω——脉动球的振动圆频率，ω=2πf；

ρ——空气密度；

k——波矢，k=2πf/c。

根据式（2-17）求平均平方声压：

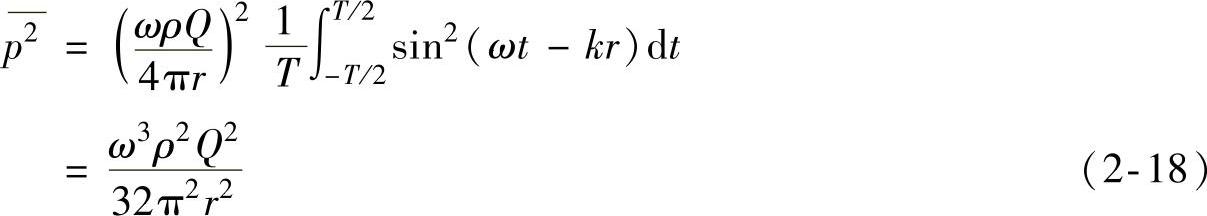
又声压与空气质点的振动速度有如下关系：

从式（2-18）、式（2-19）可得：

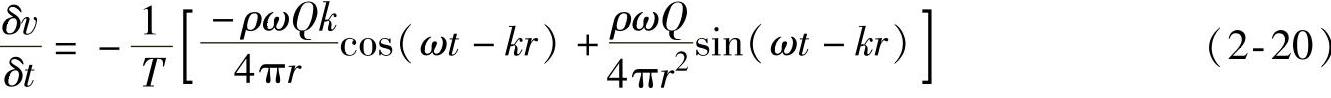
式（2-20）对时间积分则得到质点振动速度：

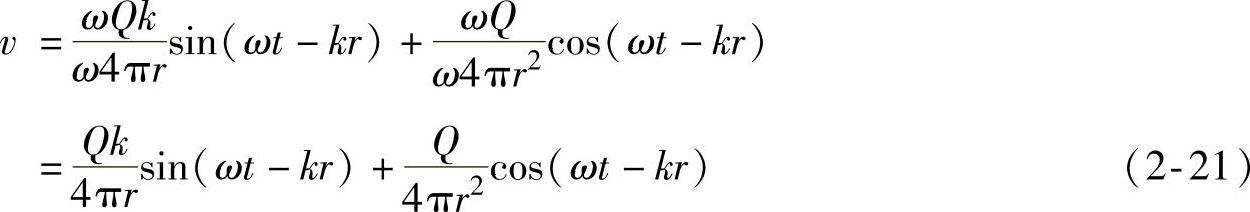
距脉动球球心距离为r处的瞬时声强为

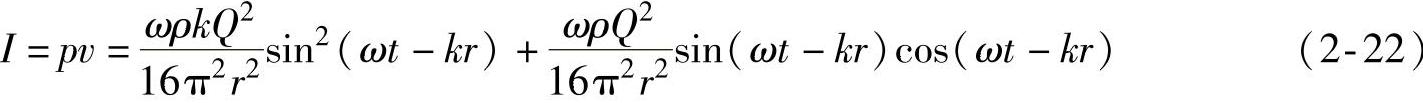
平均声强等于

比较式（2-18）与式（2-23），则有

由式（2-23）、式（2-24）看出，单极声源的平均声场强度等于平均平方声压p²与空气特性阻抗ρc之比，且与距单极声源中心距离r的平方成反比。如果在半径r的球面上对平均声强求积分，可以得到脉动球或单极声源的声功率：(www.xing528.com)

在实际生活中，有不少近似单声源辐射的例子，如笛子的发生孔，还有装在有吸声材料的匣子中的纸盆扬声器。只要把笛孔或纸盆扬声器看成一个均匀振动的整体，且尺寸远小于辐射声波波长，就可把类似于这些发声的振动物体看作单极声源。又如汽笛和火焰的燃烧吼声，也属于单极声源声辐射。注意式（2-21）中当距离r足够大时，kr＞＞1，则第二项比第一项小得多，可以忽略。与式（2-19）比较，可知质点振动速度与声压同相位，声强与质点振动速度的平方成正比，我们称这个区域为远场区，当r极小，即kr＜＜1时，式（2-21）第二项的作用比第一项强，此时声压与质点振动速度的平方成正比关系，我们称这个离声源较近的区域为近场区。

（2）偶极子声源的辐射 偶极子声源由两个相距很近、相位相反的单极声源组成。一个沿固定轴做往复直线运动的振动球，当其振幅远小于辐射声波波长时，就可当作一个偶极声源。图2-1是偶极声源的结构简图和指向图。

设偶极声源的第一个单极声源的强度为Q，两个单源相距为l，Q与l的乘积称为偶极距或偶极声源强度。显然，偶极声源是有方向性的声源，在极轴上表现出最大的声压，在垂直于极轴并通过声源中心的方向上，相位相反的两个声压互相抵消，因而声压为0。偶极声源的声场是轴对称的，只要求出距声源中心为r与极轴成θ角度方向上一点的声压，就能了解偶极声源的特点。图2-1a所示A点的声压是两个单极声源在该点声压的叠加：

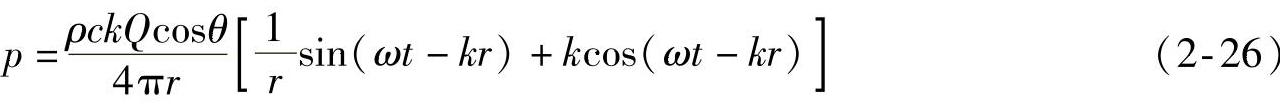
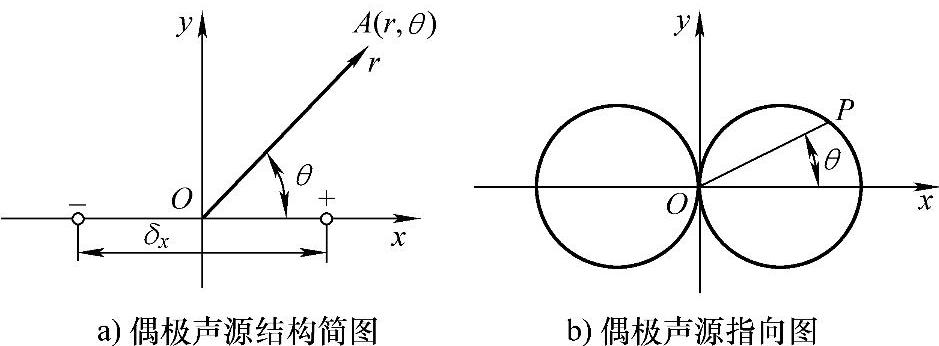
图2-1 偶极声源结构简图及指向图

从式（2-26）看出，偶极声源与单极声源相似，也有近场与远场之分，在kr＞＞1的远场区，第二项起主要作用，声压与r成反比。偶极声源声场中A点的平均声场为

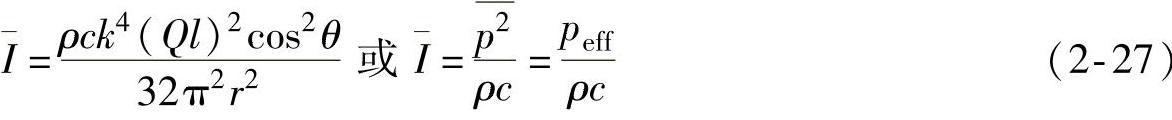
式中 p_eff——在远场区测量得到的有效声压。

偶极声源与单极声源不同，其声场有明显的方向性，但其声强只有在远场条件下测量才具有实际意义。偶极声源的声功率应当在kr＞＞1的远场区以声源中心为球心的球面上，对式（2-27）求积分得到：

偶极声源有很大一部分声压相互抵消，所以其辐射功率不如单极声源强。用式（2-28）除以式（2-25）得：

式（2-29）说明偶极声源辐射声功率在低频段，即f很小时，比单极声源辐射声功率更小。如一个没有音匣的纸盆扬声器在低频段就相当于一个偶极声源，其辐射低频声能力太弱，为了增加低频声的辐射能力，往往要把扬声器装在背面具有吸声材料的音箱中，这样扬声器由偶极声源变成单极声源，从而提高低频声辐射能力，改善音质。

（3）四极声源的辐射 四极声源有横向和纵向两种结构形式。横向四极声源由两个彼此平行的相距很近的偶极声源构成。其声场因为各单极声源之间相互干涉，所以计算和表达更为复杂，其指向图呈四个花瓣状。横向四极声源辐射的声功率为

式中 Ql₁l₂——四极声源强度。

纵向四极声源是由两个极性相反、在同一直线上的偶极声源组成。其指向图与偶极声源相似，辐射声功率为

横向的和纵向的四极声源都有近场与远场之分。声压随距离变化而变化，且四极声源比偶极声源变化更快，近区为p∞1/r³，稍远一些为p∞1/r²，远场为p∞1/r。四极声源的低频辐射能力比单极声源和偶极声源更低。喷气产生的喷射噪声属于四极声源辐射，其低频成分在射流噪声中不明显。

计算横向四极声源用等效方法，即将其等效为一对相距很近且彼此平行的反作用力偶。可将纵向的和横向的四极声源合成表示为斜四极声源，如图2-2所示。

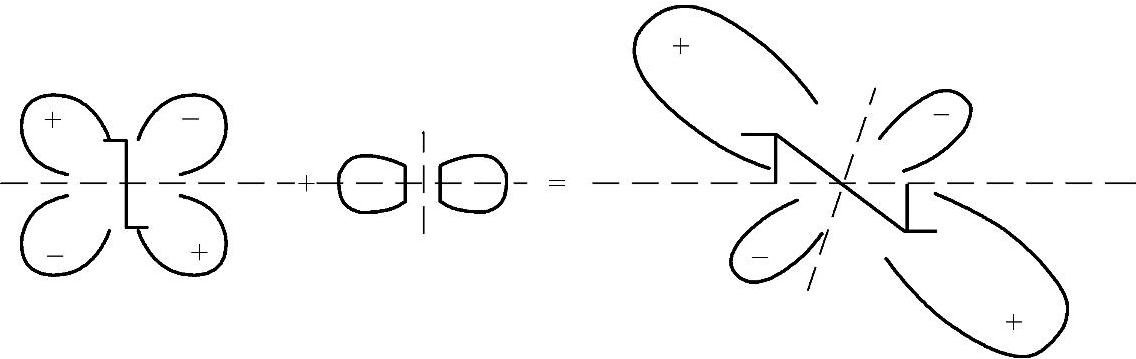
图2-2 斜四极声源与合成