动车组噪声控制技术：声压级、声强级、声功率级解析

（1）声压级 正常人耳可刚刚听到的最小声压值称作听阈（或听阈声压）。对于1kHz的基音，听阈声压值为2×10^-5Pa；使人耳产生疼痛感觉的声压值称作痛阈（或痛阈声压），其值为20Pa。从听阈声压到痛阈声压，数值相差100万倍。可见用声压的大小来表示声音的强弱是不太方便的。因为人耳听觉的灵敏度是呈对数关系变化的，所以对于声音的大小，我们将声压的变化用一个对比关系的对数量级来表示，这就是声压级。

声压级是将测得这一声音的有效声压p与参考有效声压p₀的比值的自然对数乘以20所得的数值。其数学表达式为

式中 L_p——声压级，单位为dB；

p₀——基准声压，取2×10^-5Pa。

将p₀=2×10^-5Pa代入式（2-1），则有

L_p=20lgp+94 （2-2）

由于把声压值相差100万倍的变化范围，用声压级表示，就变成了0～120dB的变化范围，从式（2-2）可知，声压级增加6dB，声压值增加1倍；声压级每变化20dB或40dB，就相当于声压值变化10倍或100倍。由此可见，在噪声控制中，如果使噪声降低20dB或40dB，其声压值的变化是相当大的。

（2）声强级 声强通常也用声强级表示，一个声音的声强级L_I是该声音的声强与基准声强之比的自然对数乘以10，其数学表达式为

式中 L_I——声强级，单位为dB；

I——声强，单位为W/m²；

I₀——基准声强，单位为10^-12W/m²。声强级和声压级之间的关系：

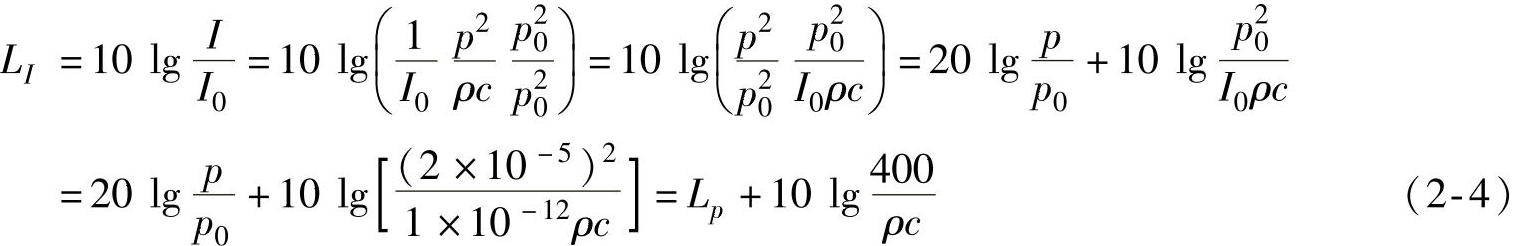
式中ρ——传播介质的密度，单位为kg/m³；

c——声速，单位为m/s；

ρc——传播介质的特性阻抗，单位为kg/（m²·s）。

从式（2-4）可以看出，当特性阻抗ρc=400kg/（m²·s）时，右边第二项等于0，声压级等于声强级。在实际中，由于右边第二项通常很小，一般认为声场中，某点的声压级在数值上等于该点声强级。空气介质中，在标准大气压和20℃时，特性阻抗ρc为408kg/（m²·s），式（2-4）末项可略，得：

L_I=L_P （2-5）

这说明在常温常压下，可认为声场中某点由同一声源所引起的声压级与声强级数值是相同的。如果知道声强级或声压级dB的变化，就可以计算出声强或声压的变化。

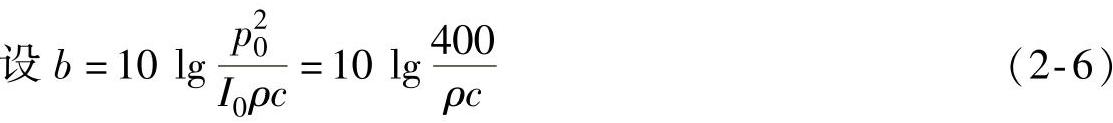
b值与声传播介质的特性阻抗ρc有关，因此，其值与气温、气压有关，其关系式为

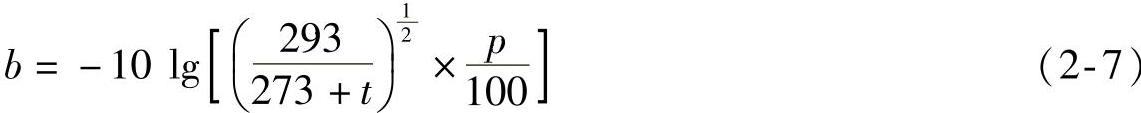
式中p——大气压，单位为kPa；

t——气温，单位为℃。

当t=20℃时，不同海拔的修正值b见表2-1。

表2-1 20℃时不同海拔的修正值b(www.xing528.com)

在使用表2-1中的数据时，当b＜0.5dB，可以忽略不计；在高原地区，b≥1dB，必须加以考虑。

（3）声功率级声压或声强只反映空间某点的声学特性，不能代表声源本身的大小，由于离声源远近不同，或声源所在的空间条件不一样，它的值也不相同。而某一声源在单位时间内辐射的总声能即声功率是一定的。因此，反映一个声源的大小特性主要用声功率表示。我们把声源在单位时间内辐射的总声能称为声功率，常用W表示，单位为瓦（W）。声功率是表示声源特性的一个物理量，声功率越大，表示声源单位时间内发射的声能越多，引起的噪声越强。声功率的大小，只与声源本身有关。声功率通常也用对数标度，即用声功率级表示。一个声源的声功率级，等于这个声源的声功率与基准声功率之比的自然对数乘以10，其数学表达式为

式中 L_W——声功率级，单位为dB；

W——声功率，单位为W；

W₀——基准声功率，单位为10^-12W。

（4）声功率级和声强级的关系 在自由声场中，对于均匀辐射的声源W=IS，其中I为声强，S为垂直于声波传播方向声源的封闭面积，单位为m²。将式W=IS代入式（2-8）得到

S₀为基准声功率对应的基准面积，一般取S₀=1m²，由此得声功率级L_W与声压级的关系式：

L_W=L_I+10lgS （2-10）

式中 S——垂直于声波传播方向声源的封闭面积，单位为m²。

对于自由声场中，球面波的半径为r时，得：

L_W=L_I+10lg4πr²=L_I+20lgr+11 （2-11）

对于点声源放在刚性反射面上，声波只向半空辐射，其波阵面为2πr²，这种声场称为半自由声场，此时

L_W=L_I+20lgr+8 （2-12）

声功率级与声压级的关系如下：

对于半球面波

L_W=L_p+20lgr+8+b （2-13）

对于球面波

L_W=L_p+20lgr+11+b （2-14）

在实际生活中，某点的噪声往往由多个声源引起。实践证明，两个及两个以上声源的总声级，不是各个声源声级的代数和。这是因为，声音的叠加是能量的叠加，而声级又是以对数值表达的缘故。

噪声叠加后的强度，应按对数的运算法则进行。如n个同样的噪声源作用在距各声源等距离的一点上时，所产生的总声强级应按下式计算：

L_Itotal=10lg（nI/I₀）=10lgI/I₀+10lgn=L_I+10lgn （2-15）

同理，按上式得出总声压级：

L_Ptotal=L_P+10lgn （2-16）