主要计算方法解析及应用in框架结构稳定性研究

目前结构的稳定分析和设计方法主要有6大类:平衡法、能量法、动力法、数值方法、有限元方法和规范的简化方法。

1)平衡法

平衡法[1]是求解结构稳定承载力的最基本方法,也称为中性平衡法或静力平衡法。对于有平衡分支点的弹性稳定问题,根据图1.3所示荷载-挠度曲线,屈曲失稳在分支点处处于临界平衡状态[类似于图1.1(c)中的小球],即以分支点为分界,一个是结构的平衡状态[类似于图1.1(a)中的小球],一个是结构的不平衡状态[类似于图1.1(b)中的小球]。平衡法是根据已产生微小变形后结构受力条件建立的平衡法方程进行求解。若平衡方程的解不止一个,那么这些解的最小值为该结构的分岔屈曲荷载。在许多情况下,采用平衡法可以获得精确解。

以图1.4所示的悬臂柱为例对平衡法进行介绍,按照弯矩平衡,对任何横截面m-n取矩得:M=-P(δ-y),于是挠度曲线的微分方程为:

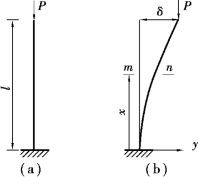
图1.4　悬臂柱

取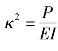,可将方程(1.3)写为:

方程(1.4)的通解为:

存在如下边界条件:

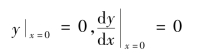
将上述边界条件代入式(1.5)可得:

利用杆顶端的存在的边界条件:,由式(1.6)可求得:

δ cos κl=0

取最小解:;由此求得:;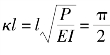

可得临界承载力:

当结构加载大于式(1.7)所求的屈曲临界荷载,结构挠度将因急剧增加失去稳定而无法继续承载。

2)能量法

能量法[11]是计算结构临界屈曲荷载的一种近似分析方法。如果结构承受着保守力,可以根据变形结构的受力条件建立变形体的总势能,总势能Π是变形体的应变能U和外力势能V之和。如果结构处在平衡状态,那么总势能必有驻值。根据势能驻值原理,先由总势能对位移的一阶变分为零,得到平衡方程,再由平衡方程求解分岔屈曲荷载。按照小变形理论,能量法一般只能获得屈曲荷载的近似解;但是如果事先能够了解屈曲后的变形形式,采用此变形形式计算则可得到精确解。

仍以图1.4所示悬臂柱为例,假定自由端作用集中荷载的悬臂柱挠度曲线为:

假定曲线符合所需端点条件,即在固定端的切线是铅直的,而在顶端的曲率为零,悬臂柱的弯曲应变能为:(www.xing528.com)

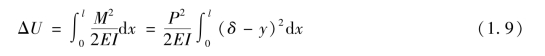
集中荷载做功为:

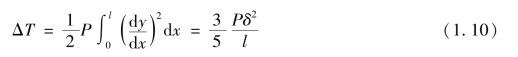
根据势能驻值原理,总势能对位移的一阶变分为零求解屈曲荷载,可得:

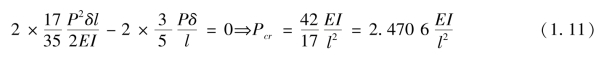
与平衡法求得的精确解误差仅为0.13%。

3)动力法

处于平衡状态的结构体系,若在外部施加一个小的外干扰,小球将发生振动,动力法[2]就是建立这种振动和已作用荷载的关系。当荷载小于稳定的极限值时,加速度和变形的方向相反,因此干扰撤去后运动趋于静止,如图1.5(a)所示的振动是收敛的,结构的平衡状态是稳定的;当荷载大于极限值时,加速度和变形的方向相同,即使将干扰撤去,运动仍是发散的,如图1.5(b)所示,因此结构的平衡状态是不稳定的;那么能够使杆件振动收敛的最大荷载就是杆件的临界荷载,临界荷载即为结构的屈曲荷载,可由结构振动频率为零的条件解得,此时振幅始终保持一样大,如图1.5(c)所示,结构处于临界平衡状态[2]。

图1.5　平衡状态的振幅图

4)数值方法

数值方法[12]在平衡法和能量法运算过程中经常使用,其中,数值积分法是常用的一种。在很多实际应用中,可能只能知道积分函数在某些特定点的取值,或者积分函数可能是某个微分方程的解,这些都是无法用求原函数的方法计算函数的积分,因此只能使用数值积分计算函数的近似值。数值积分法可将柱子进行分段,如图1.6所示,考虑节点之间及边界的变形协调和平衡关系(几何非线性),对每一节点考虑真实的弯矩-曲率非线性关系(材料非线性),通过增量加载方式得到荷载-挠度曲线,确定杆件的极限承载力,再进行截面设计。这也是本书考虑二阶效应钢筋混凝土截面承载力图解法计算的基本思路。

图1.6　数值方法的分段

5)有限元方法

在计算机性能容许的范围内,面对人工计算已经很难解决的材料非线性问题和几何非线性问题,有限元方法[13]不需要任何简化,都可以通过增量加载的方法来解决。目前,在结构整体弹性稳定计算时,有限元方法能够高效实现。若进行钢筋混凝土结构整体弹塑性稳定分析,因为需要考虑几何非线性和材料非线性,而且结构杆件众多,采用有限元软件计算是比较困难的,如何对稳定分析计算结果进行准确判断也是很重要的,假如无法对计算结果进行准确判断,会给工程结构安全带来灾难性的后果,而这些对于一般的设计人员还是很难实现的。因此,有必要寻求便于工程应用的钢筋混凝土结构整体稳定的计算方法。

6)我国规范的简化方法

我国《钢结构设计标准》[19]基于传统的计算长度系数法在附录E中给出了一些受压柱计算长度系数的计算表格,运用这些图表,很容易确定受压柱弹性稳定承载力。另外,我国《混凝土结构设计规范》[20]为基于等效矩形应力换算理论提供了钢筋混凝土矩形截面的承载力计算和配筋计算公式。该规范第6.2.4条提供了一种用弯矩增大系数来反映由P-δ效应引起的内力增长,计算式为:

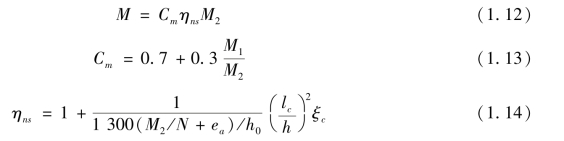
式中　Cm——等效弯矩系数;

ηns——考虑挠曲二阶效应的弯矩扩大系数;

ξc——曲率修正系数,按照下式计算:

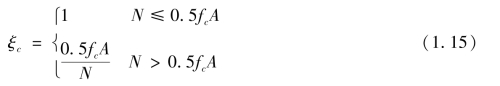
通过该方法计算求得弯矩增大系数来考虑P-δ效应的影响,将弯矩增大后再按照规范提供公式进行配筋设计。对于框架结构、框架-剪力墙结构在考虑P-Δ效应的影响时,《混凝土结构设计规范》也给出了增大系数的计算方法,但增大系数的确定需要确定框架楼层侧向刚度,而对于框架-剪力墙结构将其等效等截面的悬臂受弯构件利用顶点位移相等的原则计算结构刚度,这种等效计算相对粗糙,不能考虑框架与剪力墙的相互作用,而且并非真正意义的框架-剪力墙结构。这种方法计算稳定需要先确定构件的计算长度,而这正是稳定临界力求解的内容,其解决精度受长度计算的影响。规范法求解方法公式复杂,求解过程参数众多,计算多有不便,有必要寻求更好的求解办法。