钢筋混凝土柱稳定问题的解析计算方法研究

1)轴心受压柱:屈曲失稳

对于图1.2(a)所示的理想轴心受压柱,即假定柱子既无初始缺陷也不存在初始偏心,这种类型的受压柱失稳受到了广泛的研究,其破坏类型属于屈曲失稳,即受压柱承载力超过其极限承载力而发生失稳,此承载力的极限值称为屈曲荷载,也称为临界荷载。这一问题也称为屈曲问题或特征值问题。

图1.2　柱子类型

对于细长柱,柱子因受压屈曲丧失稳定而破坏,屈曲荷载起到了控制作用,材料应力没有达到强度应力允许值。1759年,欧拉(Euler)提出了弹性阶段柱子屈曲荷载NE的计算公式[7]:

式中　EI——柱的抗弯刚度;

lc——柱的计算长度。

式(1.1)计算受压柱临界荷载在二阶弹性分析中得到了广泛应用,虽然通常情况下受压柱存在开裂等非弹性情况,完全弹性的假设已不满足实际情况,但是由于欧拉临界力计算公式概念简单且便于应用,特引入一个变化的弹性模量,此时对应柱的抗弯刚度也发生变化,这样,欧拉公式就可用于非弹性屈曲的情况,这种方法Engesser(1889)和Considère(1891)几乎同时发现[1],先后提出了切线模量理论和折算模量理论。Shanley[3](1947)也对弹性受压柱进行了分析,他将压杆模型简化为一个中间由双弹性肢连接的刚性柱,在此基础上进行了理论推导,其研究结果验证了Engesser所提出的切线模量理论考虑非弹性稳定承载力计算的正确性。屈曲荷载NE是弹性细长柱的一个重要特征变量,是一些二阶分析方法中的重要参数。

2)偏心受压柱:极值点失稳

理想受压柱在实际上是不存在的,实际工况中的柱子可能存在初始缺陷,轴力的作用点也可能存在初始偏心,因而绝大部分的柱子都是偏心受压柱[图1.2(b)],属于极值点失稳(第二类失稳),其极限荷载也称为失稳极限荷载,也称为压溃荷载[3]。(www.xing528.com)

图1.3示意了偏心受压柱的一阶弹性、二阶弹性和二阶弹-塑性分析3种情况的荷载-变形曲线。当N=0时,柱子存在初始偏心距(e1),3种曲线的挠度变形都是从e1开始。这3种情况分别是:

第1种情况:采用一阶弹性分析时,荷载作用与变形之间是线性关系,所以在图1.3中为一条直线。

第2种情况:采用二阶弹性分析时,荷载作用和变形不再是线性关系而是非线性关系,当材料为弹性时,曲线趋近于屈曲荷载。

第3种情况(极值点失稳):采用二阶分析且材料为弹塑性时,曲线的极限承载力大为降低,曲线由上升段和下降段组成,极限荷载位于极值点。从N=0开始,变形随着荷载作用的增大而增大,变形逐渐进入塑性阶段,曲线斜率下降,变形快速增加,当荷载作用达到极限值(极值点),变形曲线进入下降段,荷载必须下降才能维持内力和外力的平衡。这种变化特性也被称为量变失稳[5]。

图1.3　柱的荷载-挠度曲线

3)钢筋混凝土柱的失稳

对于轴心受压的钢筋混凝土柱,大部分情况在轴力较小时混凝土就开裂了,混凝土的开裂和钢筋的屈服后,材料表现的必然是非弹性性能,此时钢筋混凝土柱的刚度将不再是弹性刚度,应为弹塑性刚度,随着塑性开展而逐渐降低,承载力也随之降低。我国《混凝土结构设计规范》(GB 50010—2010)[20]给出了一种采用折减系数对柱承载力进行折减的计算方法,以此来体现弹塑性开展后结构刚度的变化,利用钢筋混凝土稳定系数φ来考虑这种降低,在试验和理论推导的基础上得到了一个稳定系数计算公式:

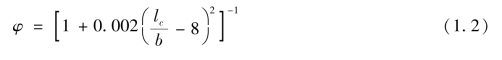
式(1.2)是在试验和理论推导的基础上得到的,该系数仅与长细比有关,若要求解长细比需要确定构件的计算长度,而计算长度问题又属于临界力计算的问题。