1.基于伪随机序列自相关性的新型超声波测距系统
超声波传感器具有成本低廉、结构简单、体积小等特点，可应用于汽车防撞、机器人路径规划、工业距离测定、水位液位量测和混凝土结构探伤等领域。超声波测距利用的是超声波近似直线传播和反射的特性，目前常用的是单脉冲激励式。虽然这种方法应用比较广泛，但其存在如下缺陷：①在实际测距过程中，环境中温度、湿度、气压对超声波的传播速度都会产生影响；②温度变化的影响最大，用340m/s代替超声波传播的速度必将引入测量误差；③超声波回波信号是一个调制信号，无明确的回波信号前沿，因而在确定渡越时间的过程中，其基准点的选择已成为测量误差的主要来源；④噪声与回波同时被接收，即使电路中带有滤波电路，与脉冲频率相近的噪声依旧无法滤除，这将造成误触发。上述问题已成为制约利用超声波测距的瓶颈。
伪随机序列是一个具有一定周期的取值为0和1的离散码序列，它具有与随机噪声相似的尖锐自相关函数特性，但它并非真正随机，而是按一定的规律周期性变化的序列。m序列是伪随机序列的一种，是由移位寄存器反馈连接产生的最大线性长度的序列，其特征多项式为
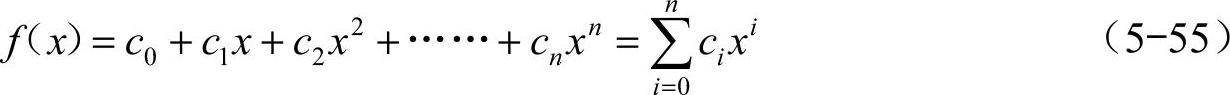
两个长为N的实离散时间序列x（n）与y（n）的互相关函数可由式（5-55）计算得出，即
式中，τ为延迟时间。
由式（5-56）可得m序列的自相关函数rxx（τ）为分段函数：当τ=0时，rxx（τ）=1；当τ≠0时，rxy（τ）=1/P，P为m序列的周期。
当伪随机序列的周期足够大时，其自相关函数具有尖锐的二电平特性，接近于δ函数。基于伪随机序列自相关性的新型超声波测距系统中，正是利用伪随机序列尖锐的自相关函数特性，来测量发射码和接收码之间的延时，从而计算出渡越时间。在测量的过程中，绝大多数噪声与伪随机序列都不相关，这些噪声都可以通过计算收发序列的相关函数来抑制。
（1）新型超声波测距系统的测距原理 新型超声波测距系统由三个模块组成：渡越时间确定模块、超声波传播速度实时测量模块和信息融合模块。基于伪随机序列良好的自相关特性，超声波测距系统可准确地测量出超声波的传播速度和渡越时间，进而计算出障碍物的距离。
1）渡越时间的确定。基于m序列良好的自相关性来测定渡越时间，渡越时间测定的过程如下：由TMS320VC5509A DSP产生的m序列通过通用I/O引脚输出，激励超声波发射电路将其转换成对应的超声波信号发射出去，超声波遇到目标会反射回来，超声波接收模块将其滤波、放大后，通过序列还原模块还原成对应的离散序列，与本地码发生模块产生的m序列进行相关运算。记录下相关函数值取值最大时，本地m序列与接收到信号的还原后m序列的相位差N，渡越时间Tr可由式（5-57）计算得出，即
Tr=NW （5-57）
2）超声波传播速度的实时测量。渡越时间实时测量模块是由一对超声波换能器和长方体目标组成。一对超声波换能器用于收发超声波，长方体目标距超声波换能器的距离已知，设为d。超声波换能器在发射电路的激励下产生超声波，发出的超声波遇到长方体目标后反射回超声波换能器，该过程渡越时间Tr0的测定原理如上文所述。则超声波实时的传播速度可由式（5-58）计算
3）信息融合模块。信息融合模块主要由TMS320VC5509A DSP组成，TMS320VC5509A是TI公司生产的一种高性能、低功耗的定点DSP。其主要负责m序列的生成、相关运算及障碍物距离的计算。障碍物的距离S可由式（5-59）计算
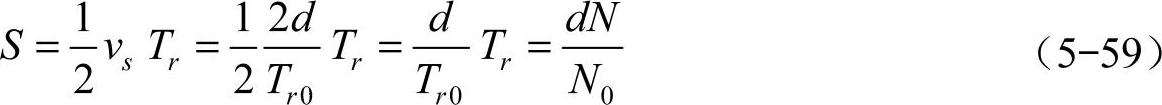
（2）新型超声波测距系统的硬件电路 新型超声波测距系统的硬件电路主要包括三部分：发射电路、接收电路和数据采集电路。硬件电路原理如图5-34所示，其中由TMS320VC5509A DSP把存储在其内部的伪随机码作为使能信号加到NE555定时器上，控制NE555发射出带有伪随机二进制序列的信号来驱动超声波换能器。当由NE555发出高电平信号时，超声波换能器发出信号；当NE555发出低电平信号时，超声波换能器就不发出信号，从而实现用伪随机序列信号调制超声波信号。回波到达超声波换能器后经过前端放大、带通滤波、后级放大、整流电路、采集电路后，以脉冲的形式回到TMS320VC5509A DSP中。
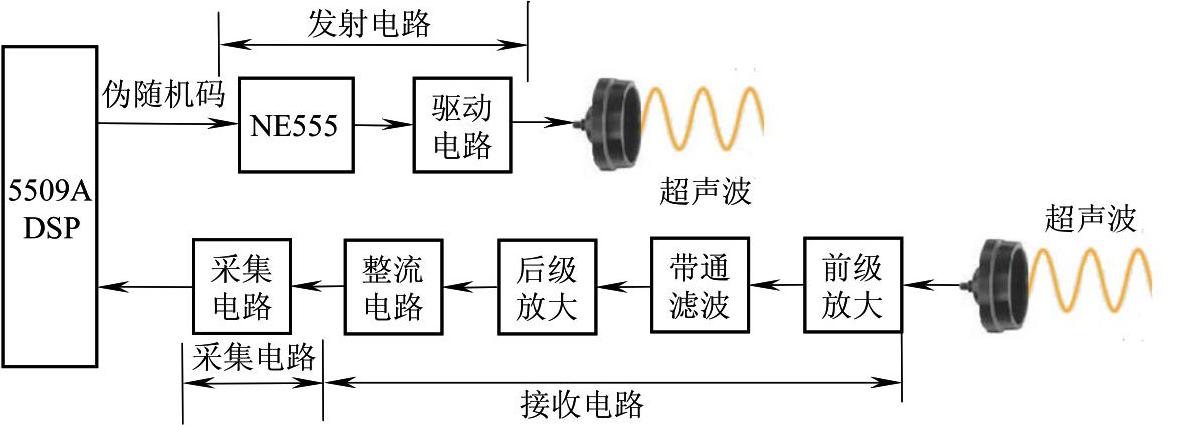
图5-34 新型超声波测距系统硬件电路原理
图5-35所示为新型超声波测距系统的发射电路，激励信号源由一个NE555定时器发出，伪随机码作为调制信号由DSP发出，接到NE555的使能管脚上，由NE555定时器发出40kHz的方波信号。NE555发出的激励信号经过一个NPN/PNP型晶体管的互补功率放大电路，直接加到一个由MOSFET构成的放大电路上。MOSFET实质上是高速开关器件，受到输入输出间的耦合、配线等寄生电感的影响而不稳定，因此必须插入一个门极电阻R4。为了保证MOSFET能够很好地实现开关动作，在其前级采用了NPN/PNP型晶体管互补功率驱动电路。在与DSP的接口处用光耦进行隔离，光耦在这里起到保护和匹配电压的作用。
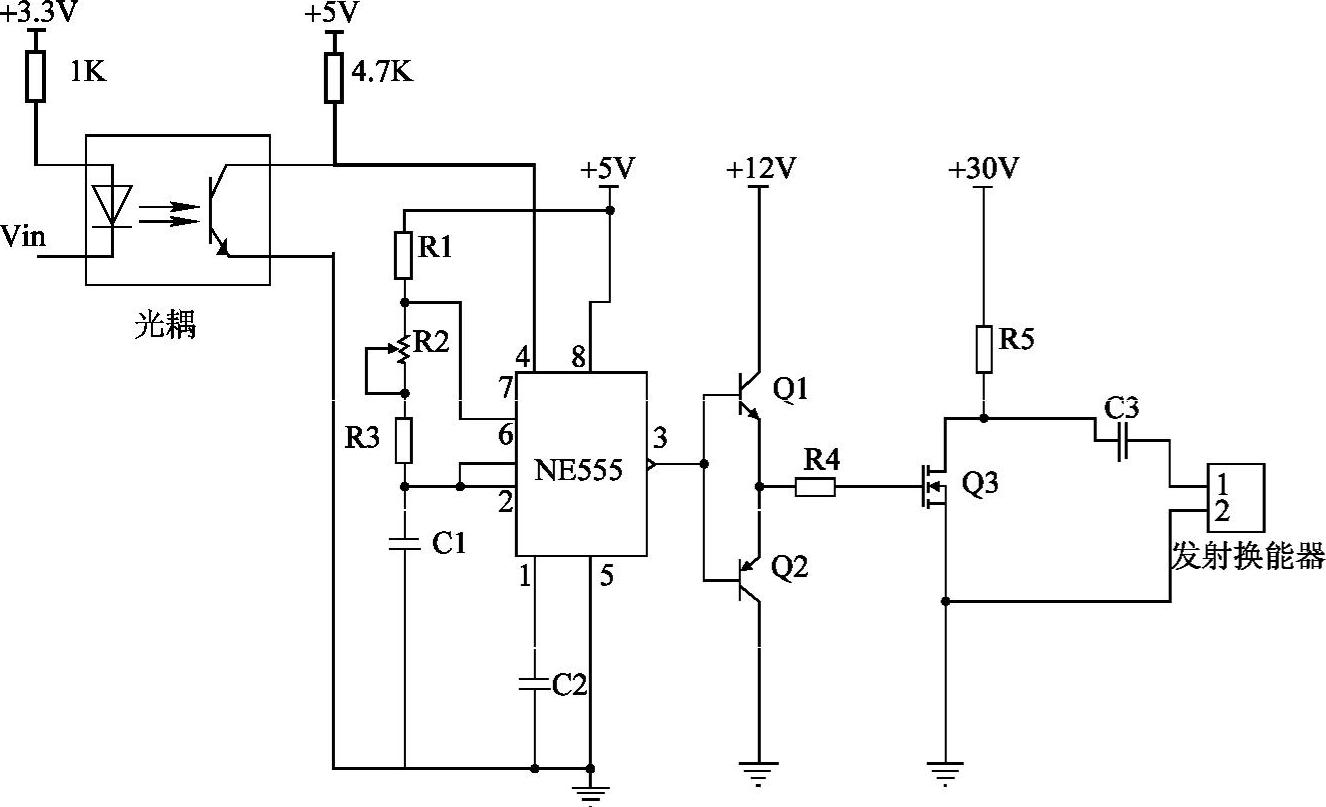
图5-35 新型超声波测距系统的发射电路
接收电路分为四个部分，分别是前级放大电路、带通滤波电路、后级放大电路、高速化的绝对值电路。
前级放大电路的原理如图5-36所示。由于超声波传感器输出的信号十分微弱，属于mV级，因此必须先进行前级放大。采用仪表放大器AD620对采集到的信号进行放大，放大倍数为100倍。
带通滤波电路部分为一个压控电压源的二阶带通滤波器，如图5-37所示。因为超声波信号的中心频率为40kHz，所以带通滤波器的中心频率f0也选为40kHz。将相关的数据代入，经计算可得带通滤波器的带宽为2.069kHz，品质因数Q=19.3，具有良好的选择性。
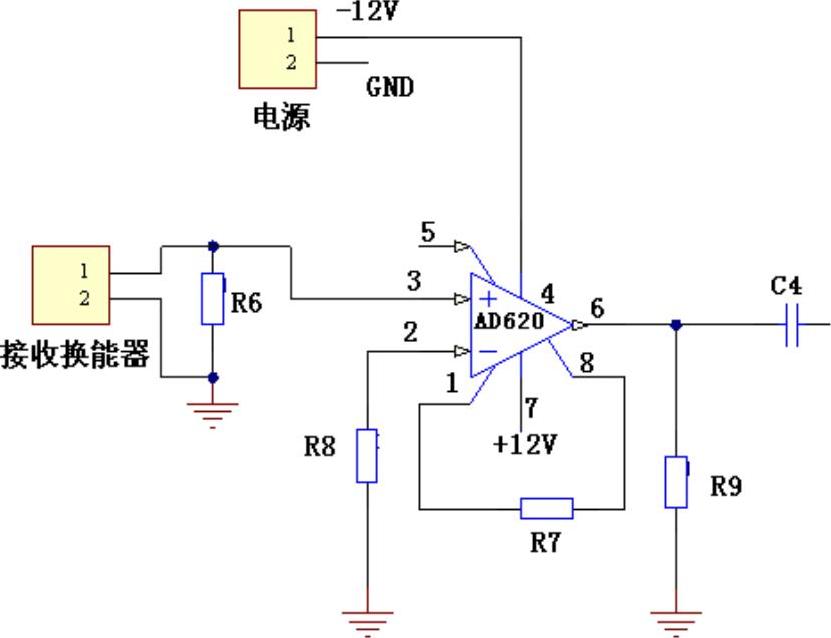
图5-36 前级放大电路
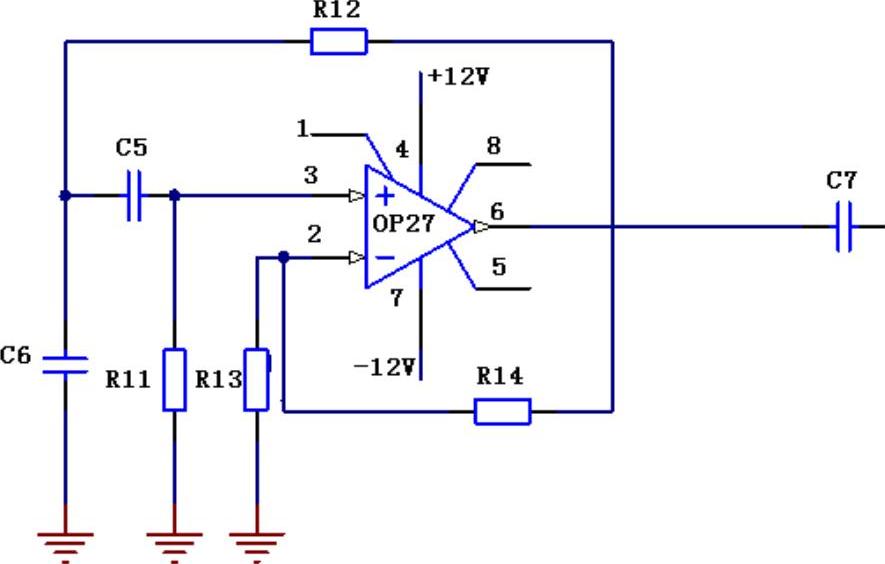
图5-37 带通滤波电路
后级放大部分是对滤波后的信号进一步放大，目的是把信号放大到可以被后续电路进行处理的程度，采用集成运算放大器对滤波后的信号放大10倍。
通过后级放大器所接收到的超声波回波信号是带有伪随机序列的信号，采用高速化绝对值转换电路将伪随机序列从超声波形中解调出来。通过高速化绝对值电路能够把回声信号处在负半轴的部分转到正半轴，以提高信号的有效值，从而得出所需要的伪随机序列。高速化绝对值转换电路如图5-38所示，当输入信号为负时，VD1截止，VD2导通，U1为倒相放大器，U2为正向放大器；当输入信号为正时，VD1导通，VD2截止，U1为倒相放大器，U2也为倒相放大器。因此无论输入信号的电压极性如何，其输出总是正电压，且幅值不变。如前所述，超声波回波信号经过绝对值变换电路以后，负电压被翻转为正电压，且频率倍增，然后通过二极管VD3、电容C10组成的检波电路对新波形进行包络。
回波信号携带着伪随机序列的信息，而数据采集的目的就是要从超声波的信号中把伪随机序列提取出来。伪随机序列属于低频信号，所以采用采样频率为100kHz的MAX164作为模数转换芯片，图5-39为MAX164与DSP5509A的硬件连接图。如图5-39所示，把MAX164的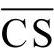
与DSP芯片的CE3管脚相连，从而把MAX164的地址映射到CE3空间；将McBSP1的FSR引脚（S12）配置成GPIO与MAX164的BUSY相连，用于读取ADC的状态位；用DSP的地址线A0与MAX164的
相连，用于控制启动模数转换。采用Slow Memory模式，并行读入数据；时钟采用外部时钟模式，在MAX164外加一个晶振，其输出端与MAX164的CLKOUT、CLKIN分别相连。
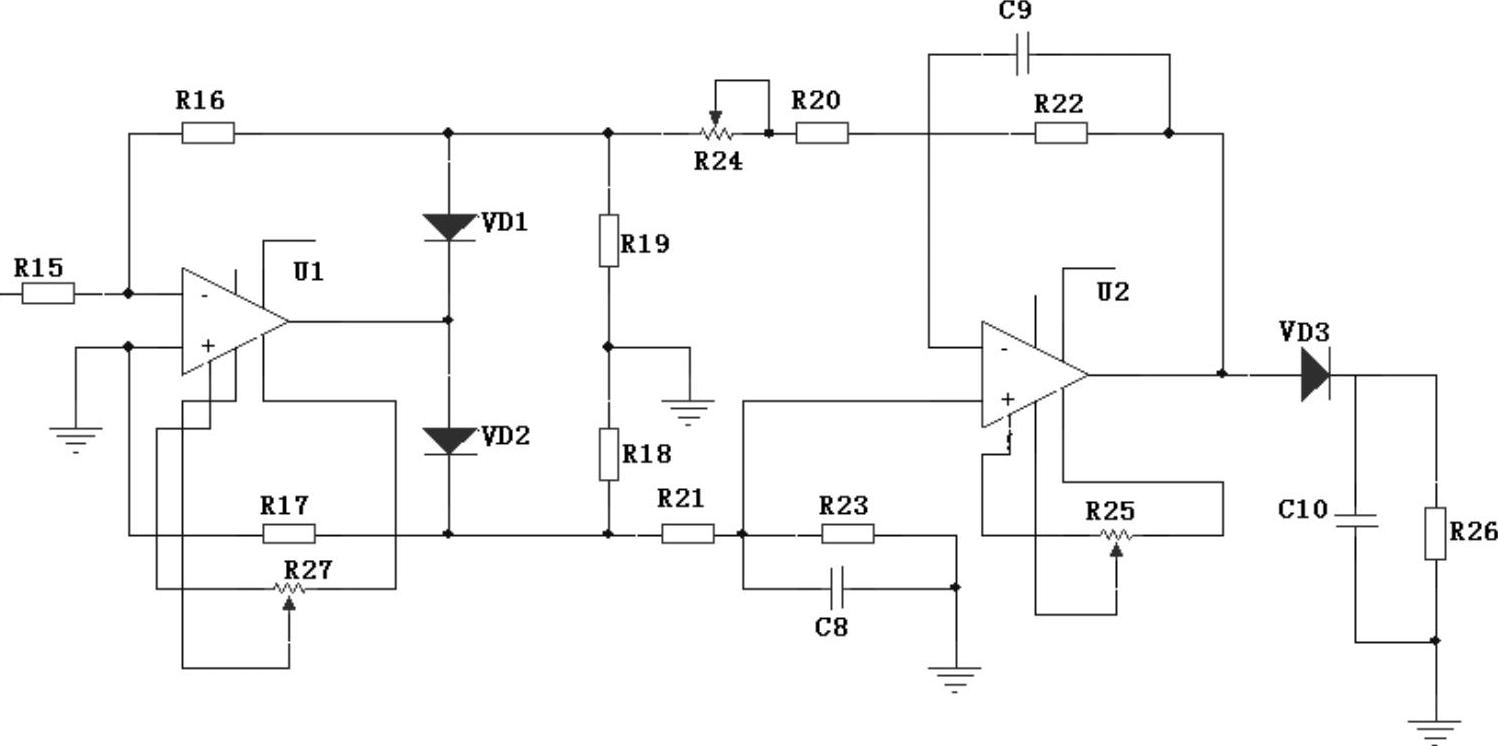
图5-38 高速化绝对值转换电路
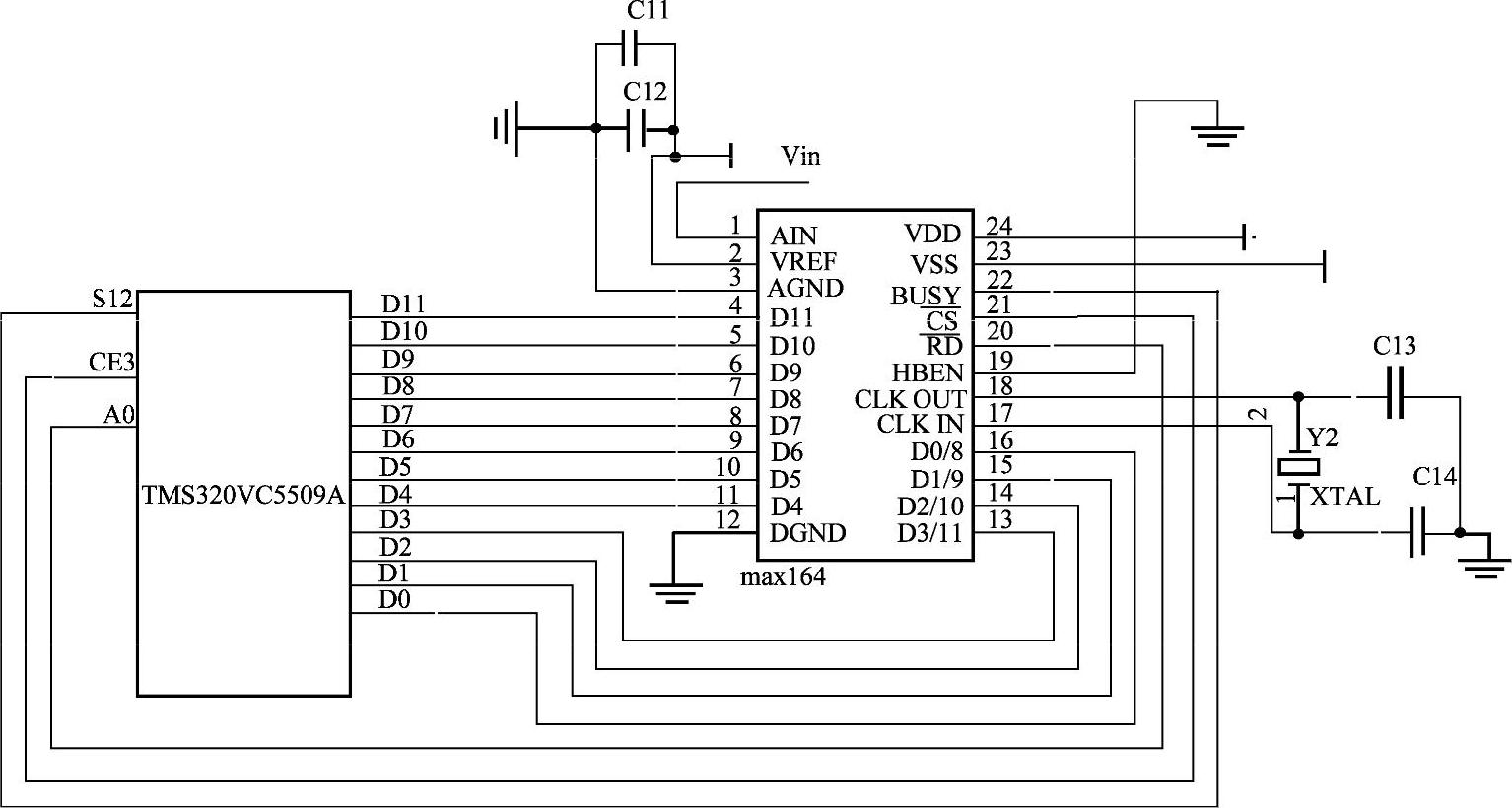
图5-39 MAX164与DSP5509A的硬件连接图
（3）新型超声波测距系统的软件设计 新型超声波测距系统的软件部分主要实现以下几个功能：一是控制超声波换能器发出携带伪随机序列的超声波信号；二是采集回波信号；三是进行相关性判别并计算出渡越时间；四是计算障碍物的距离。
整个软件系统包括两层循环：外层循环是用来输出各个传感器的距离值；内层循环是用来判别采集到的数据是否满一个周期，当采集到的数据达到一个周期以后，系统便置位标志位，关闭定时器中断和外中断，此时也就停止了数据的发射与接收，并开始顺序执行相关判断程序和距离计算程序，最后输出距离值，并且清除标志位，进行下一次同样的循环。
如何准确、快速地进行相关性判别是新型超声波测距系统软件设计的核心。采用基于快速傅里叶变换（FFT）的相关判别算法来判断本地码序列和接收到的序列是否相关，以提高相关判别的实时性，具体步骤如下：
1）将本地码序列x（n）进行FFT求得X（k）。
2）将采集到的回波进行采样得到离散序列y（n），将该离散序列进行FFT求得Y（k）。
3）计算Rxy（k）=X（k）Y（k）。
4）对Rxy（k）进行快速傅里叶逆变换，得rxy（τ），并判断rxy（τ）是否有峰值脉冲出现，若有峰值脉冲出现，则跳转到步骤5），否则跳转到步骤2）。
5）计算时延。
若伪随机序列的长度为N，直接采用式（5-56）进行相关性判别运算，其运算量为N2次实数乘法和N2次实数加法。采用基于FFT的相关判别算法可使计算量降至（3Nlog2N+N）次乘法和（3Nlog2N+N）次加法。采用TMS320VC5509A DSP作为相关函数的运算单元，其数据处理能力强大，芯片内部具有硬件乘法器，提供专门的FFT指令，使得FFT算法实现的速度很快，有效地提高了实时性。
（4）新型超声波测距系统的测距误差补偿 由于收发电路和信号处理器在对信号的处理过程中均会对回波信号产生一定的影响，产生一个固定的时延Δt，从而产生一定的测量误差。对系统的延迟时间的校正算法如下：
设L1、L2为两个已知的固定距离，超声波在这两个固定的距离中传播的渡越时间为t1、t2，则超声波在L1、L2距离内往返传播所需要的时间实际上分为t1−Δt和t2−Δt。
由式（5-60）、式（5-61）可得
在计算超声波传播的渡越时间的过程中，需要将采集到的一个周期序列与本地序列进行相关性判别运算，在每次运算中算出的结果都取码元宽度的整数倍。但在大多数情况下，超声波在空气中渡越时间都不是码元宽度的整数倍，这样就造成了测量结果偏大。这个误差的最大值为一个码元宽度的时间所传输的距离，最小值为0。为了减小误差可以在每一个测量结果上减去半个码元时间所传输的距离，这样就可以把计算渡越时间产生误差的最大值减小到半个码元时间内超声波传输的距离。
（5）性能测试实验与分析 基于伪随机序列自相关性的新型超声波测距系统的原理样机如图5-40所示。
在进行新型超声波测距系统硬件电路的测试时，伪随机码的周期为15，码元宽度为1ms，该序列为“1，1，1，1，0，0，0，1，0，0，1，1，0，1，0”。由DSP数字信号处理器的GPIO口发出的伪随机序列，经过光耦隔离后，在示波器上的显示波形如图5-41所示。经放大电路后的驱动信号效果如图5-42所示，驱动波形为经过伪随机信号调制的方波信号，并且达到了预期的放大效果，虽然经过放大后的波形与原波形反向，但是作为驱动信号，这不影响超声波换能器的正常工作，其能够顺利地把伪随机序列加载到超声波信号上。
图5-40 新型超声波测距系统的原理样机
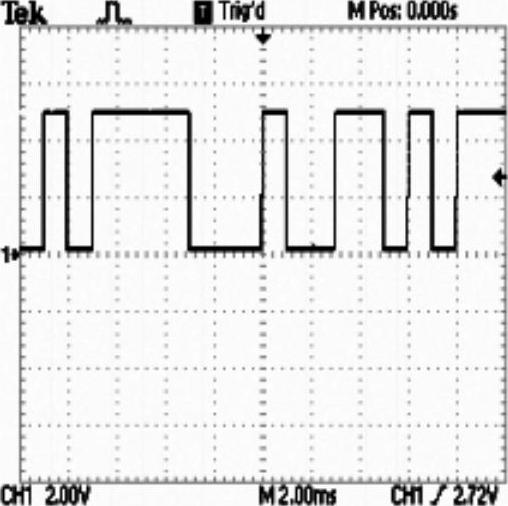
图5-41 DSP所发出的伪随机序列
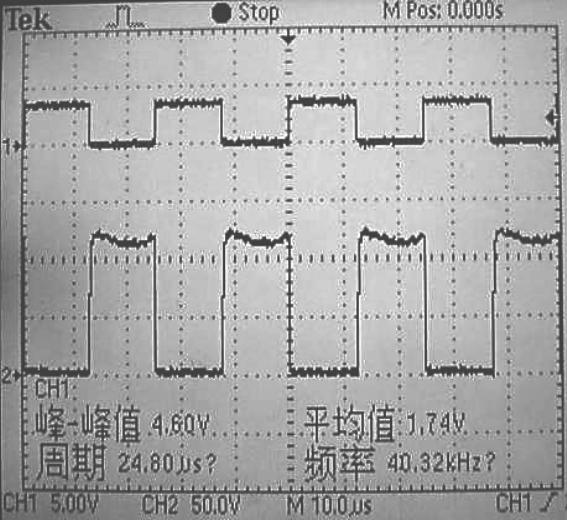
图5-42 放大后的驱动信号
超声波接收换能器接收到的信号是40kHz的正弦波信号，经过放大、滤波和高速绝对值化电路得到的波形如图5-43所示。由图5-42可知，通过高速绝对值化电路之后，降低了余波的拖尾现象，使系统采样得到的信号更加准确。通过观察图5-42的包络波形，可知图中两条红线之间的部分便是一个周期的伪随机序列，其数值为“1，1，1，1，0，0，0，1，0，0，1，1，0，1，0”，这个结果和DSP发出的伪随机序列完全吻合，从而验证了系统硬件设计的正确性与可行性。经过A/D转换后的回波信号与本地码序列作相关运算的结果如图5-44所示，尖峰脉冲出现在相位为12的时候。
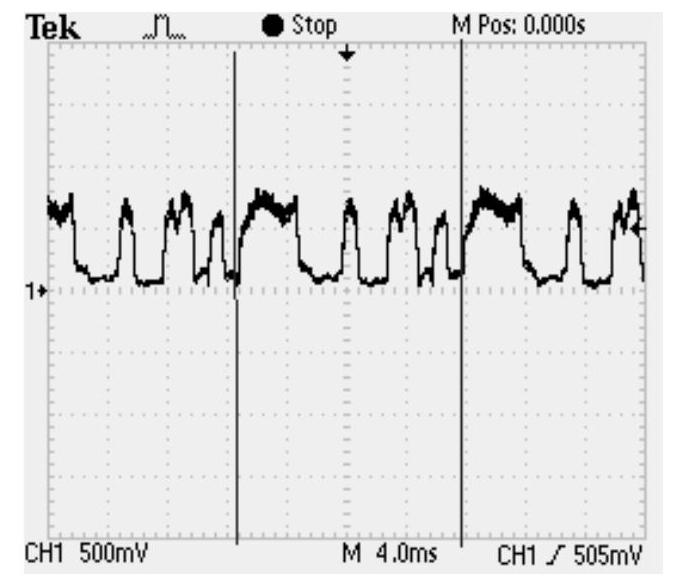
图5-43 经过高速绝对值化电路得到的波形
新型超声波测距系统的原理样机的距离测量实验在温度为20.2℃，湿度为42.5%的环境中进行，在此实验环境中人为地加入了与超声波频率相近的噪声，所加入噪声的频率范围为37～43kHz。新型超声波测距系统测得的超声波在此环境下传播344.6m/s。从实验结果可以看出，在测量距离为0.4～5.0m新型超声波测距系统的范围内，测距误差在1.8%以内，且具有良好的抗干扰性。
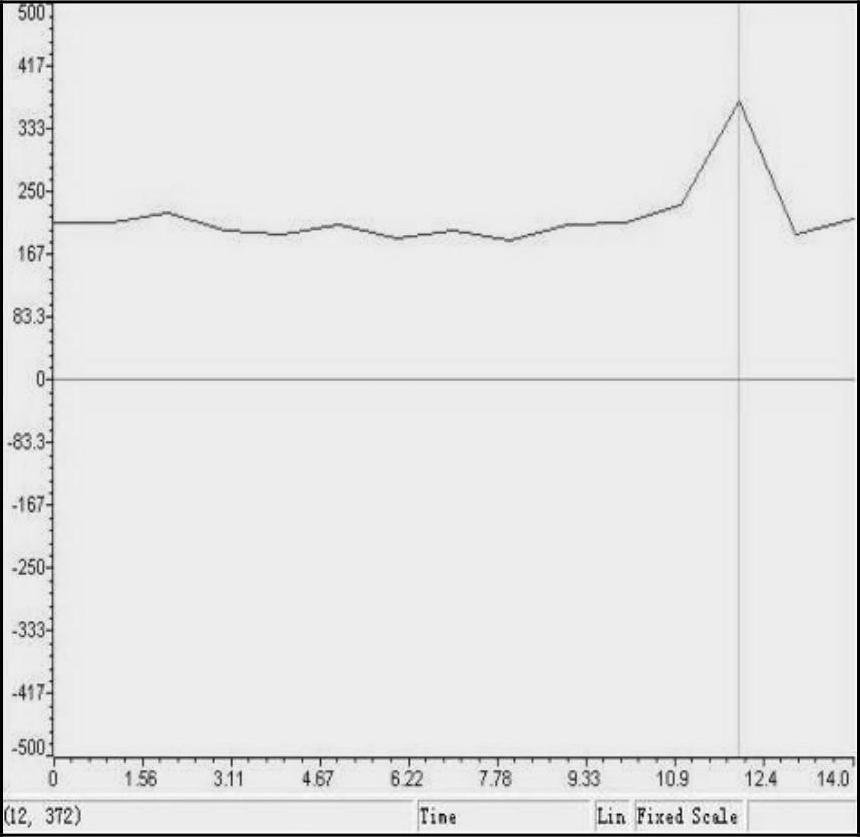
图5-44 相关运算结果
导航技术是特种机器人的关键技术之一，也是特种机器人实现智能化的基础。准确确定自身的位置是特种机器人适应环境、进行自主作业的前提。精度高、抗干扰能力强、实时性好是对特种机器人导航系统的基本要求。
为提高导航的精度和抗干扰能力，机器人常常将多种导航器件有机组合、互补使用，并采用卡尔曼滤波算法对组合导航系统的参数进行校正。仿生六足机器人采用GPS/INS组合导航系统。GPS全球定位系统以空间卫星为基础来实现导航与定位，具有全天候、全球覆盖、全方位、高精度等特点，且没有时间积累误差，但采用GPS技术进行单独导航时，在有遮挡物的环境中容易产生“丢星”现象。INS系统能不依赖外界信息，完全独立自主地提供多种导航参数，但是导航参数的误差会随时间积累，不适用于长时间单独导航。将GPS器件和INS器件进行有机地组合，可以各取所长。当GPS信号受到高强度干扰或当卫星系统接收机出现故障时，INS系统可以独立地进行导航定位。高精度的GPS信息可以用来修正INS，控制其误差随时间的积累。
基于GPS/INS的组合导航系统可用如下一阶线性状态方程（5-63）和量测方程（5-64）表示，即
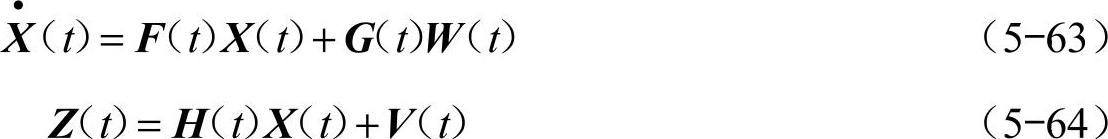(www.xing528.com)
式中，X（t）为系统状态矢量；F（t）为系统的状态矩阵；G（t）为系统的动态噪声矩阵；W（t）为系统的过程白噪声矢量；Z（t）为系统的量测矢量；H（t）为量测矩阵；V（t）为系统的量测噪声矢量。取状态矢量为
X=[δLδλδhδvEδvNδvUϕEϕNϕUεrxεryεrz ∇x ∇y ∇z]T
其中，δL、δλ、δh表示经度、纬度、高度的误差；δvE、δvN、δvU表示东、北、天空方向的移动速度误差；ϕE、ϕN、ϕU表示东、北、天空方向的航向姿态角误差；εrx、εry、εrz表示随机漂移；∇x、∇y、∇z表示加速度计零偏。
选择GPS/INS的位置、速度观测信息来组成量测方程。INS的位置量测信息可表示为地理坐标系下的真实值与相应误差之和。
GPS接收机输出的位置量测信息，可表示为地理系下的真实值与相应的误差之差。
式中，Lt、λt、ht分别为机器人在大地坐标系中的实际位置；NN、NE、Nh为GPS接收机沿东、北、天空方向的位置误差；RM为地球参考椭圆球子午圈上各点的曲率半径，RM=Re（1-2f+3fsin2L）；RN为地球参考椭球卯酉圈上各点的曲率半径，RN=Re（1+fsin2L）；Re为地球椭圆长半轴；f为地球椭圆扁率。
位置量测矢量定义如下
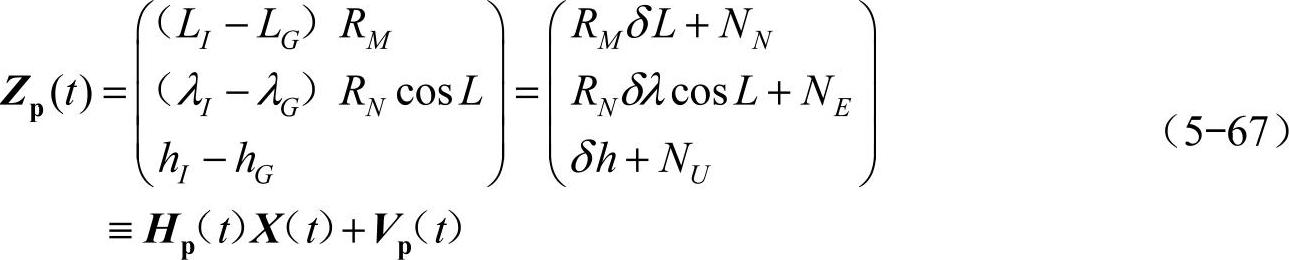
INS的速度量测信息可表示为地理坐标系下的真实值与相应的速度误差之和。
式中，vE、vN、vU是机器人在地理坐标系下东、北、天空方向上的真实速度。
GPS的速度量测信息可以表示为地理坐标系下的真实值与相应的速度误差之差。
式中，ME、MN、MU为GPS接收机的速度测量误差在东、北、天空坐标轴上的分量。
速度量测矢量定义如下
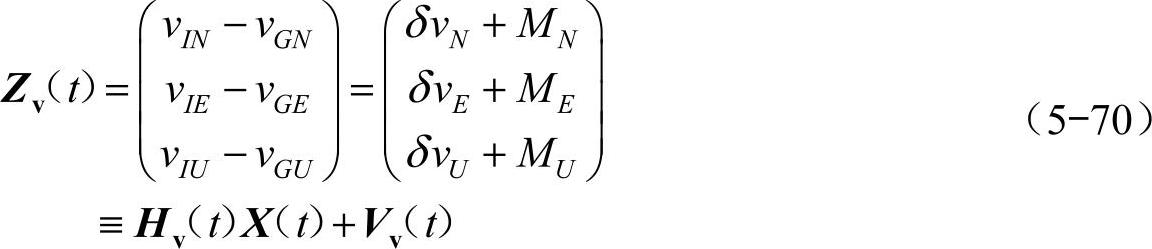
由位置测量矢量式（5-67）和速度测量矢量式（5-70）可得基于GPS/INS导航系统的位置、速度量测方程
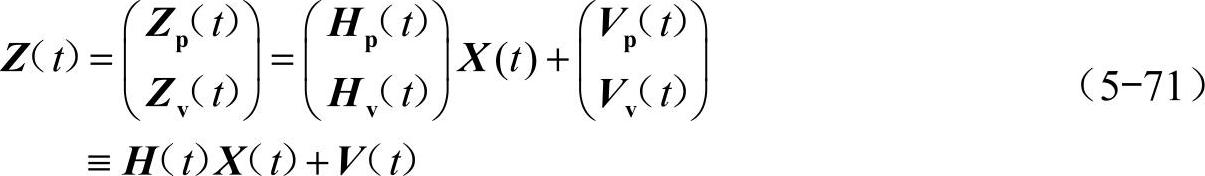
位置量测矢量的噪声标准差为
速度量测矢量的噪声标准差为
式中，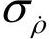
为GPS接收机的伪距测量误差的标准差；
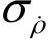为GPS接收机的伪距测量率误差的标。准差；HDOPN为GPS接收机输出的北方向上的水平位置精度因子；HDOPE为GPS接收机输出的方向东上的水平位置精度因子，VDOP为GPS接收机输出的垂直位置精度因子。
由式（5-72）、式（5-73）可知，导航系统的量测噪声主要由GPS接收机的伪距测量误差、伪距率测量误差、GPS接收机输出的水平位置精度因子和垂直位置精度因子决定。GPS接收机的伪距测量误差、伪距率测量误差与GPS接收机的软件解算算法及其硬件性能水平相关，因此对于确定类型的GPS接收机可认为其伪距量测误差和伪距率量测误差是一个定值，而水平精度因子和垂直精度因子是时变的，其随捕捉到卫星的数目和位置情况而变化。因此，GPS接收机输出的水平位置精度因子和垂直位置精度因子是影响基于GPS/INS导航系统数学模型中量测噪声改变的重要因素。
为提高导航系统的抗干扰能力，获得更加精准的导航参数，对导航器件输出的信息进行滤波是必要的。采用卡尔曼滤波时，如果滤波模型与实际系统不符，不能真实地反映物理过程，使模型与获得的量测值不匹配，就会产生滤波误差，甚至可能发生滤波发散现象。因此，有必要对卡尔曼滤波进行实时的在线调整，防止滤波发散。
为反映滤波模型和观测数值的匹配程度，定义残差
式中，Zk为离散化后在k时刻的量测矢量；Hk为离散化后在k时刻的量测矩阵；Xk为离散化后在k时刻状态矢量，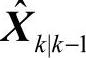
为Xk的一步估计。残差序列方差的理论值Dk和实测值Fk可分别由式（5-75）、式（5-76）确定
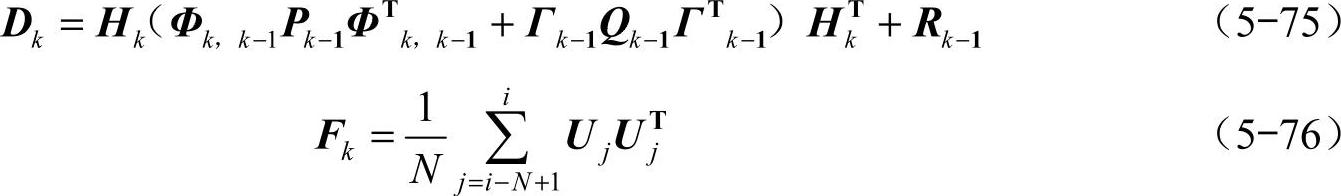
在理想状态下，残差序列{Uk}的均值为零，其方差的实测值Fk与经过卡尔曼滤波得到的方差的理论值Dk应该是相等的，即它们的比值为1或接近1。如果该比值长期偏离1，则说明量测噪声已经发生了变化，需要对量测噪声协方差矩阵Rk进行调整。
由前面的分析可知，GPS接收机输出的垂直位置精度因子VDOP与水平位置精度因子HDOP影响量测噪声的变化。位置精度因子PDOP与垂直位置精度因子VDOP和水平位置精度因子HDOP的关系为
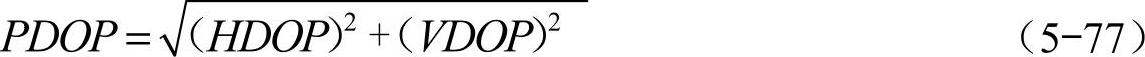
因此，位置精度因子PDOP也是调整量测噪声协方差矩阵Rk的重要依据。
基于上述分析，提出一种级联二阶模糊自适应卡尔曼滤波算法对基于GPS/INS的机器人组合导航系统进行滤波。如图5-45所示，将GPS和INS输出的位置和速度信息的差值作为滤波器的输入，并实时监测滤波情况。当滤波至时刻k时，如果发现滤波异常，则滤波模型已不宜用于当前的实际系统。此时，应对k时刻的量测噪声矩阵进行调整，以适应当前的系统。调节因子由两部分构成，分别根据残差序列的统计信息和GPS接收器输出的位置精度因子PDOP来确定。构造级联二阶模糊逻辑控制器，第一阶模糊逻辑控制器的输入量是残差序列方差的实测值与理论值的比值，输出一个初步的调节因子Sk；第二阶模糊逻辑控制器输入量是Sk的值及GPS接收器输出的位置精度因子PDOP，输出为置信度调节因子α，最终的调节因子为Sαk（Sk＞0，α≥0）。
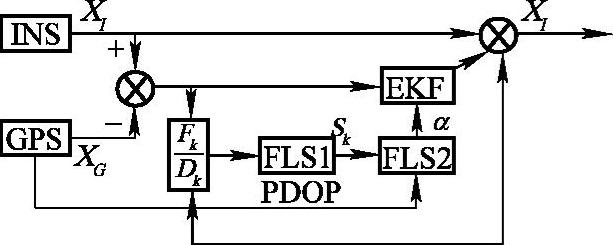
图5-45 级联二阶模糊自适应卡尔曼滤波器的原理图
根据上述原理，级联二阶模糊自适应卡尔曼滤波器的滤波过程可由式（5-78）～式（5-83）递推实现。
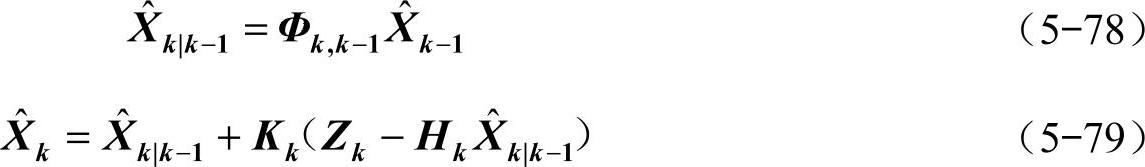
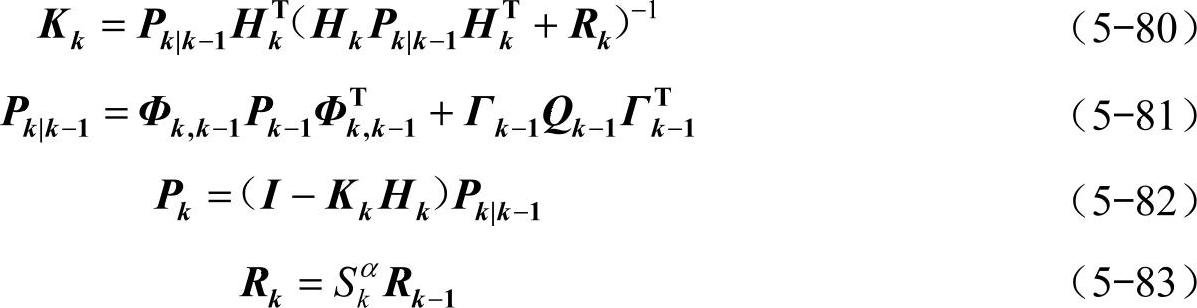
式中，Kk为增益矩阵；Pk为估计误差的协方差矩阵；Γk−1为离散后的系统噪声矩阵；I为单位矩阵。
模糊化、模糊推理和去模糊化是模糊逻辑控制器设计的核心步骤。用于确定初步调节因子Sk的第一阶模糊逻辑控制器输入为残差序列方差的实测值与理论值的比值，输出为初步调节的精度因子Sk。输入、输出的隶属度函数如图5-46和图5-47所示。采用近似于梯形的渐变隶属度函数，是为了避免输入在近似理想的情况下，FLS仍然调节滤波因子而出现滤波误差的问题。
当残差序列方差的实测值Fk逐渐大于其理论值Dk时，即两者的比值大于1，这时，应当增大Dk以保持滤波模型与实际相符，通过增大Rk可以达到该目的，因此应当给Sk赋一个较大的值，反之则应给Sk赋予较小的数值。因此，第一阶模糊逻辑控制器的推理规则如下：
1）如果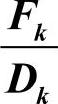
小于0.9，则Sk小于1。
2）如果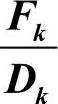
大于0.9且小于1.1，则Sk等于1。
3）如果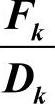
大于1.1，则Sk大于1。
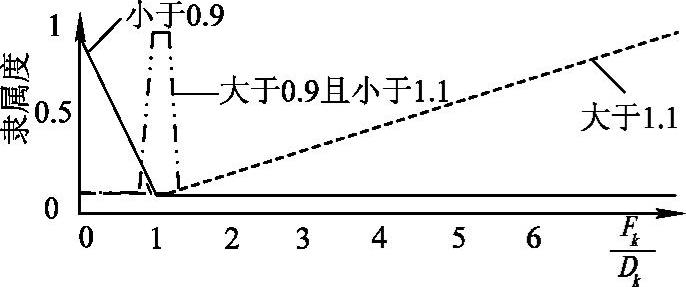
图5-46 第一阶模糊控制器输入的隶属度函数
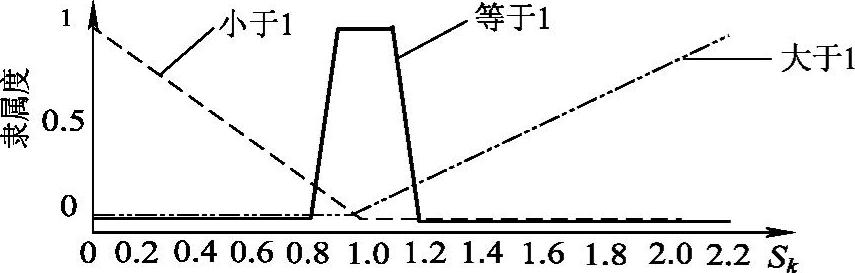
图5-47 第一阶模糊控制器输出的隶属度函数
用于确定调整因子α的第二阶模糊逻辑控制器的输入为GPS接收器输出的位置精度因子PDOP和第一阶模糊逻辑控制器的输出Sk，输出为调整因子α。PDOP仅取决于卫星在空间的几何分布。PDOP较大，GPS定位误差较大，此时，应取较小的α，以减小对测量值的置信度；反之，则取较大的α。输入、输出的隶属度函数如图5-48～图5-50所示。
第二阶模糊逻辑控制器的推理规则如下：
1）如果Sk大于1，且PDOP为好，则α大于1。
2）如果Sk大于1，且PDOP为中，则α等于1。
3）如果Sk大于1，且PDOP为差，则α小于1。
4）如果Sk小于1，且PDOP为好，则α大于1。
5）如果Sk小于1，且PDOP为中，则α等于1。
6）如果Sk小于1，且PDOP为差，则α小于1。
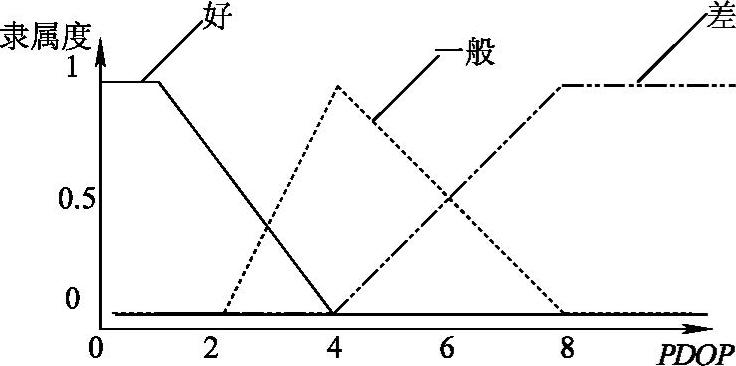
图5-48 第二阶模糊控制器PDOP的隶属度函数
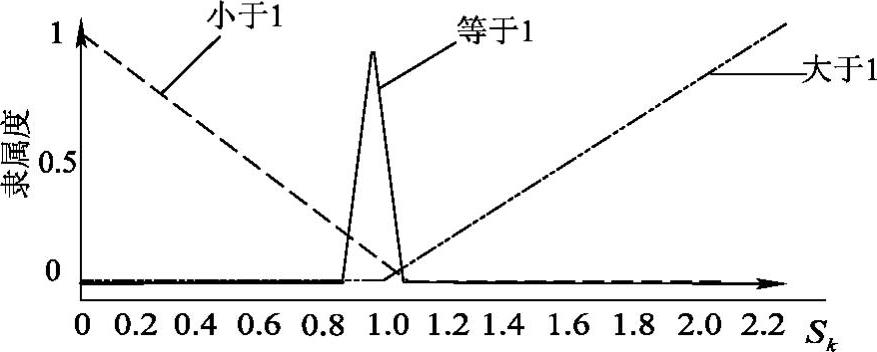
图5-49 第二阶模糊控制器Sk的隶属度函数
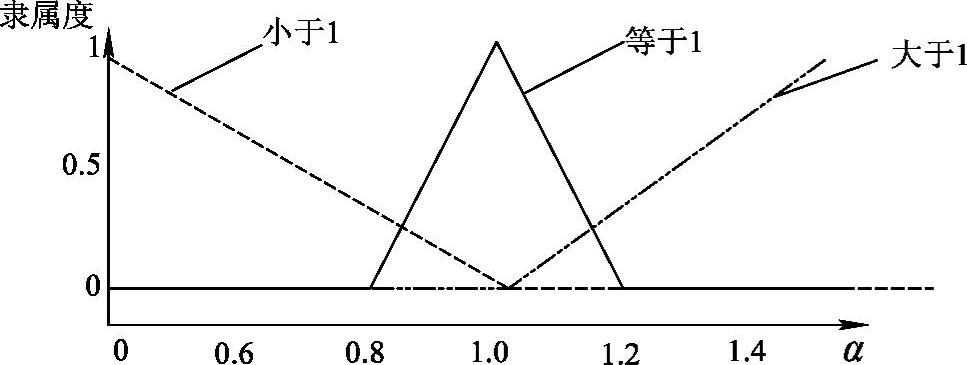
图5-50 第二阶模糊控制器输出的隶属度函数
图5-51是采用常规卡尔曼滤波与级联二阶模糊自适应卡尔曼滤波算法的滤波效果对比。从仿真结果中可知：当噪声不发生变化时（前50s），两种滤波算法的定位误差均有收敛的趋势，滤波效果曲线几乎重合，但当加入时变噪声时（50～1000s），采用级联二阶模糊自适应卡尔曼滤波算法的导航系统的精度和稳定性优于采用常规卡尔曼的导航系统。这是由于当量测噪声时变时，采用常规卡尔曼滤的导航系统的量测噪声模型并没有随之改变，造成滤波模型与实际不符，因而出现了较大的误差和不稳定性。而所提出的级联二阶模糊自适应卡尔曼滤波算法根据残差序列的统计信息和GPS接收器输出的位置精度因子的变化情况，通过级联二阶模糊逻辑控制器实时修正滤波器的滤波调节因子，不断地改变量测噪声的模型，能够反映实际滤波的物理过程，因而其滤波性能优于常规卡尔曼滤波算法。
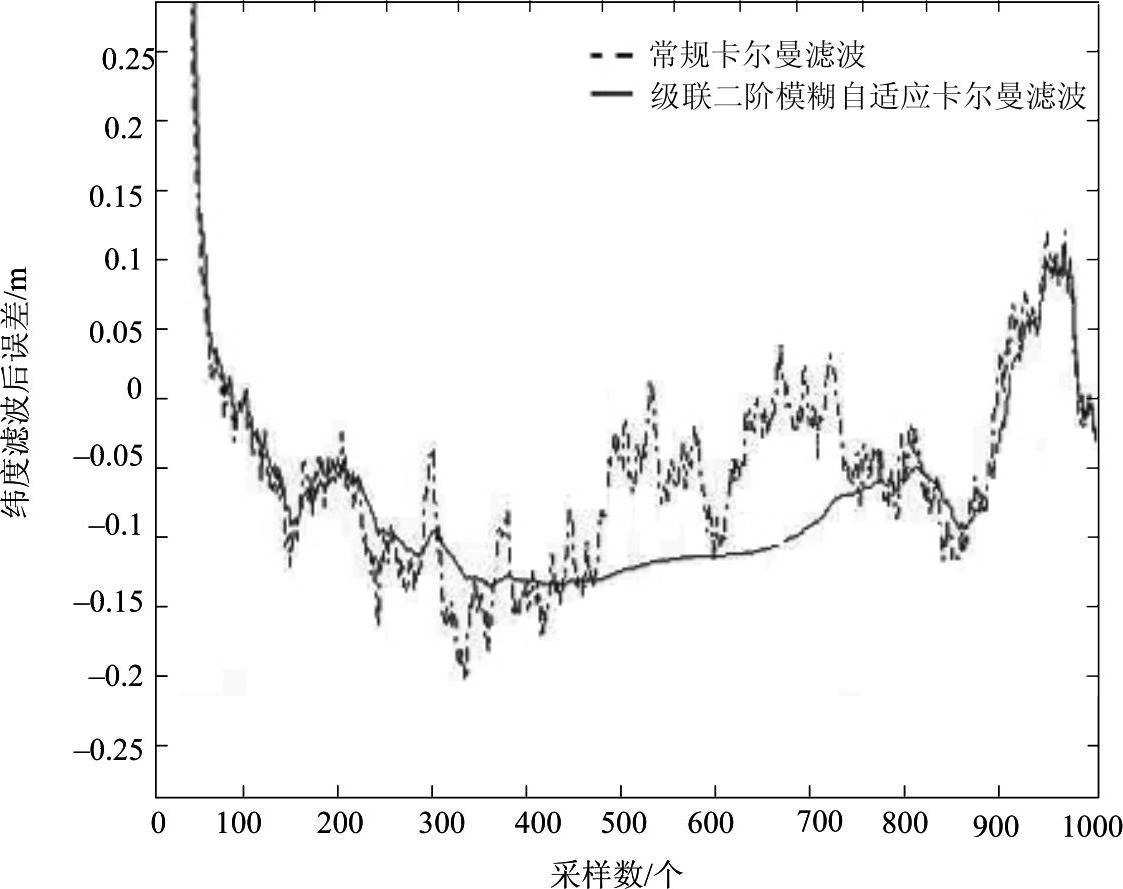
图5-51 常规卡尔曼滤波与级联二阶模糊自适应卡尔曼滤波算法的滤波效果对比
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
