大学生科技竞赛获奖作品分析:机器人运动学

1.机器人的位置分析

对机器人进行运动学分析，必须建立机器人各部件之间、机器人与周围环境之间的运动关系，用于描述机器人的操作，即要规定各种坐标系来描述机器人与周围环境的相对位姿关系。总的来说，这些坐标系包括了绝对坐标系和相对坐标系两种，机器人的绝对坐标系即大地坐标系，是建立在工作现场地面上的坐标系；机器人的相对坐标系则有躯体坐标系、关节坐标系和足端坐标系等。

（1）摆动相各腿位置分析 仿生六足机器人行走过程中，处于摆动相的各条腿相当于机械手臂，即从根关节开始由依次串联的腿节构成，因此求解各条腿上驱动关节与足端的关系，就要确定各腿节之间的相对运动和位姿关系。首先，根据Denavit-Hartenberg方法在各腿节下端（关节处）固结一个坐标系；然后，用变换矩阵建立相邻两腿节之间的相对位姿关系；最后，将各变换矩阵相乘就得到驱动关节转角与足端位姿的关系。

仿生六足机器人的运动学正解是已知机器人躯体的位姿和各腿驱动关节的转角来求解机器人足端的运动规律。图5-25表示出了仿生六足机器人腿部的D-H坐标系，各坐标系的原点O_i为关节轴线S_i与相邻关节间公垂线a_i-1,i的交点，x_i轴与公垂线a_i-1,i重合，z_i轴与关节轴线S_i重合，而y_i轴可以用右手螺旋法则来确定。图中，θ₁、θ₂、θ₃分别表示根关节、髋关节和膝关节的转角，λ表示基节中心线与根关节轴线之间的夹角，l₁、l₂、l₃分别表示基节、股节和胫节的长度。当腿部坐标系被规定后，就得到了各腿节的常量参数，见表5-2。θ_i为关节转角，a_i为腿节长度，α_i为关节轴线的扭角，d_i为公垂线之间的距离。

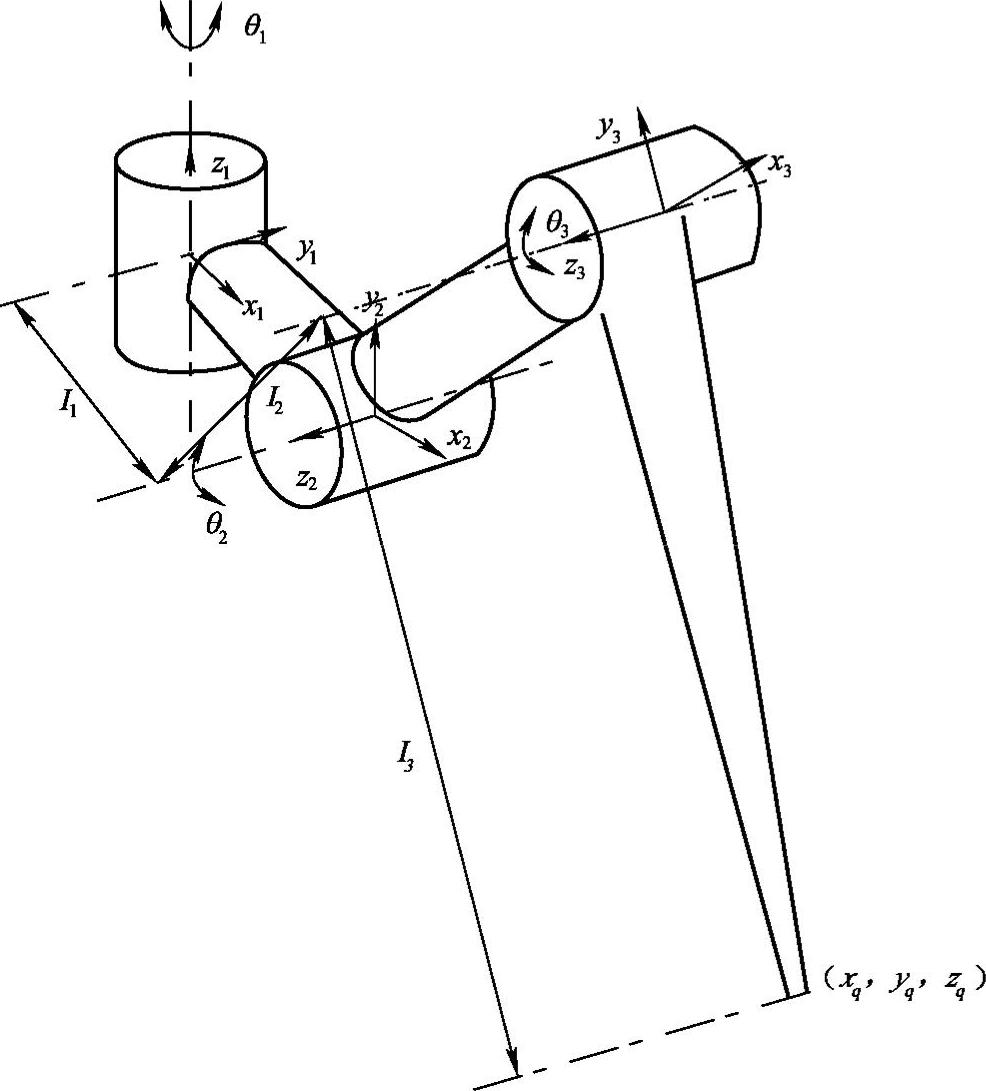
图5-25 仿生六足机器人腿部的D-H坐标系示意图

表5-2 仿生六足机器人各腿节常量参数

根据相邻两关节坐标系之间的转换矩阵

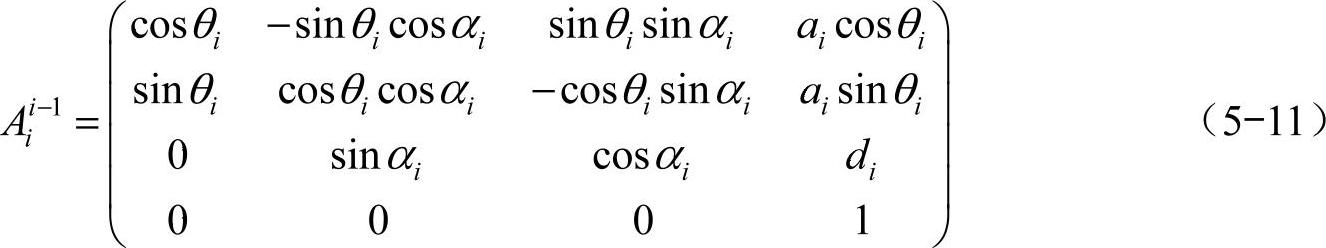
将上述D-H参数代入，可求得相邻关节坐标变换矩阵为

以根关节处坐标系作为基坐标，将相邻关节变换矩阵相乘，即可得到足端固联坐标系的转换矩阵为

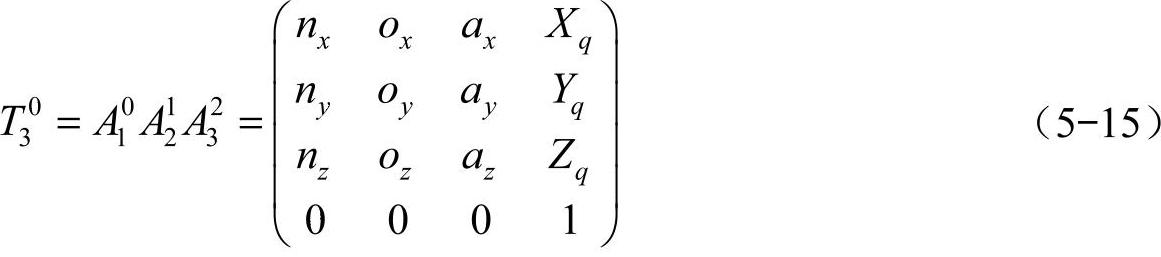
因此，由式（5-15）可得到机器人足端位置坐标为

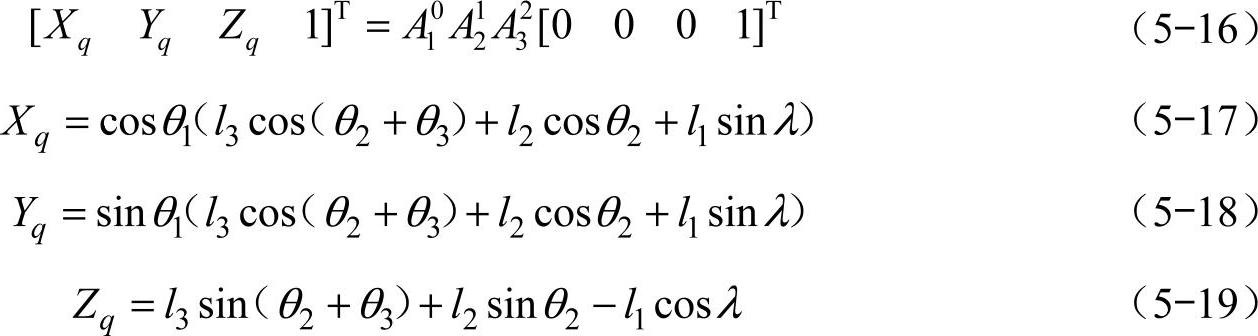
仿生六足机器人的运动学逆解是已知躯体的位姿和足端的位姿求解处于摆动相各驱动关节的转角，这里采用逆变换矩阵左乘方程两边的方法，将关节变量分离出来，从而求得关节转角。可以由（A⁰₁）^-1T⁰₃=A¹₂A²₃求得，且转角θ₂、θ₃的取值根据实际情况验证确定。

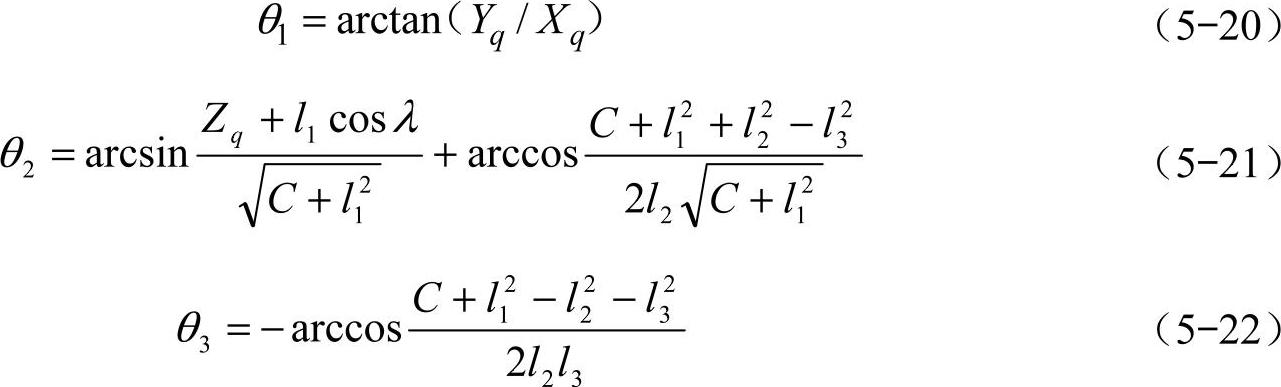
其中

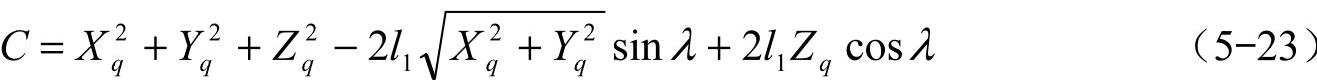
（2）支撑相各腿位置分析 仿生六足机器人行走过程中，处于支撑相的各腿与躯体构成了并联多环机构，此时已知支撑相各腿的关节转角求解躯体的位置姿态属于并联多环机构正解问题；反之，已知躯体的位置姿态求解支撑相各腿的关节转角，则属于并联多环机构逆解问题。

首先，在机器人躯体中心位置建立一个固联坐标系，则躯体的运动便可以用固联坐标系相对于大地坐标系的位置姿态变换矩阵表示

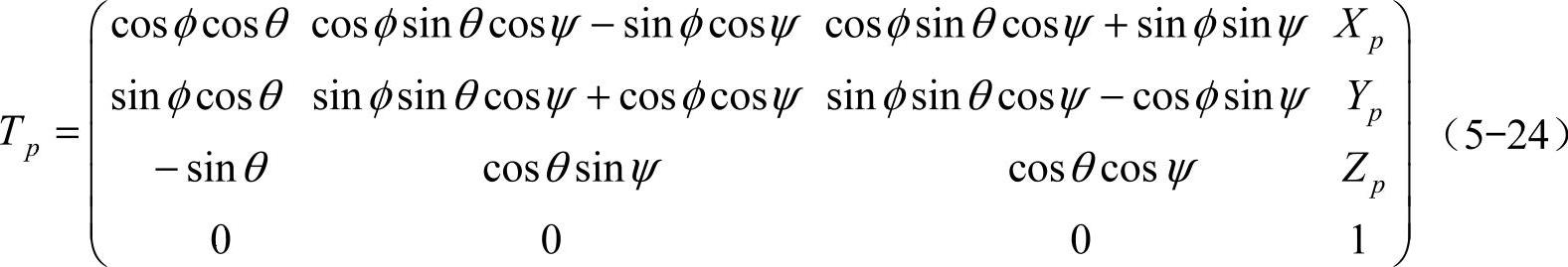
式中，X_P、Y_p、Z_p为机器人躯体坐标系原点在大地坐标系中的坐标，用以表示沿大地坐标系三轴正向移动的距离；θ、φ、ψ为绕三轴正向的转角，用以表示躯体姿态的变化。

同时，躯体的运动也可以用固联坐标系X、Y、Z三轴正向单位矢量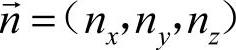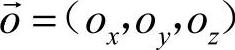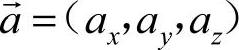，，在大地坐标系内的投影来表示，又有

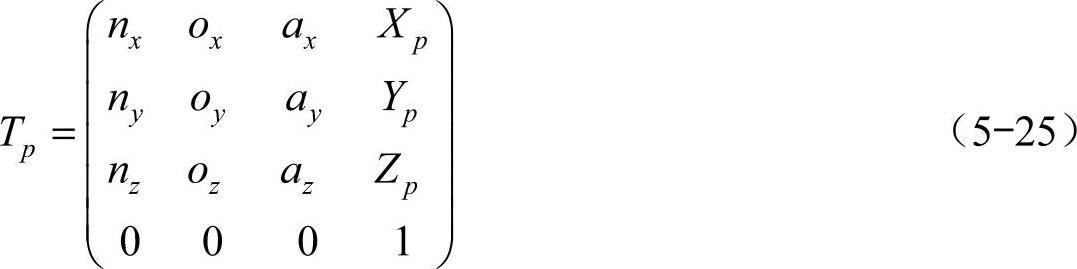
在给定机器人支撑相各腿的关节转角后，各关节之间的变换矩阵皆为已知，则有

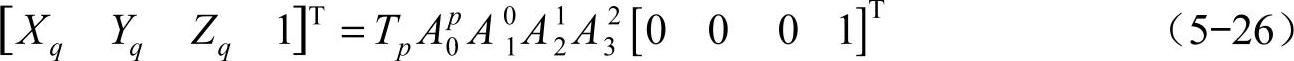
式（5-26）的左端[X_qY_qZ_q 1]^T表示足端的绝对坐标，为给定的已知条件；等式右端除T_p外，其余各项用[μνω 1]^T表示。其中，A^p₀为根关节坐标系与躯体坐标系之间的变换矩阵，假设着地腿i根关节坐标是（X^（i）₀，Y^（i）₀，Z^（i）₀），则有

当1、3、5号腿着地时，对应足端位置的坐标可分别以（X_iY_iZ_i 1）^T（i=1，3，5）表示，将以上三足的对应方程联立后可得

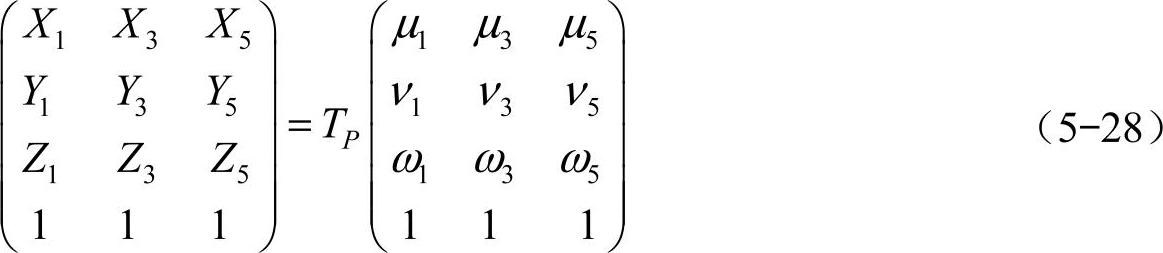
式（5-28）右端各列[μ_iν_iω_i 1]^T（i=1，3，5）分别含有各对应足紧邻躯体的关节转角θ¹₁、θ³₁、θ⁵₁，这些转角为引入中间位置量。T_P中含有表示躯体位姿的六个独立变量（待求）。对应于式（5-28）中有9个代数方程，9个位置量，理论上是可解的，但使用常规方法难以奏效。这里，可作如下处理：

先列出如下公式：

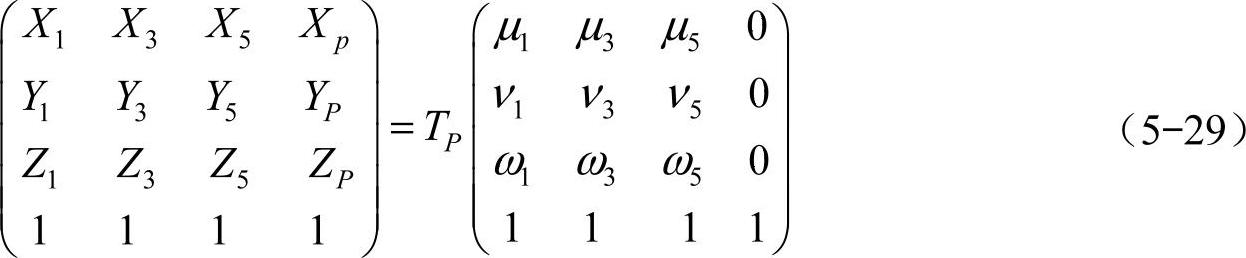
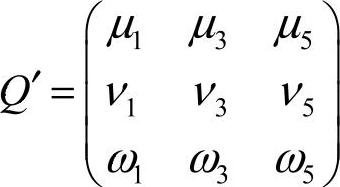而式（5-29）若要有解，需有为非奇异阵，即为非奇异阵，此时可设

则有

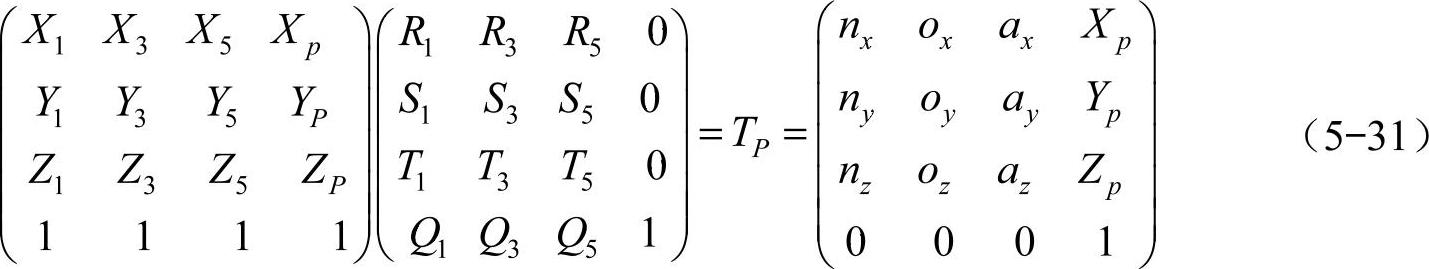
由此即可求出仿生六足机器人的躯体位置和姿态。同样，已知躯体的位置姿态，根据以上公式也可以求出机器人支撑相各腿的关节转角。

2.机器人的速度分析

要实现对机器人的精确控制，只了解位置参数是不够的，还需要对其运动参数进行分析。运动分析是在已知机器人的机械结构和几何尺寸的条件下，建立其运动参数之间的运动关系式，包括速度分析和加速度分析两个方面。由于加速度分析与速度分析类似，在这里仅对机器人的速度进行分析。

可参照机器人位置分析的方式对机器人进行速度分析，这可分两步完成。首先按串联机构对机器人摆动相各腿进行速度分析，然后再对躯体和支撑相各腿组成的并联多环机构进行速度分析。

（1）摆动相各腿速度分析 由仿生六足机器人位置关系的分析可以获得摆动相足端空间x与关节空间q的位移关系x=x（q），将其两边对时间t求导，即可得到

式中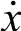，为足端空间的广义速度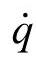；为关节速度；J（q）为雅可比矩阵，它是串联机构上某点的速度与关节角速度的线性变换，也可以看成从关节空间向足端空间运动速度的传动比，其第i行第j列元素为

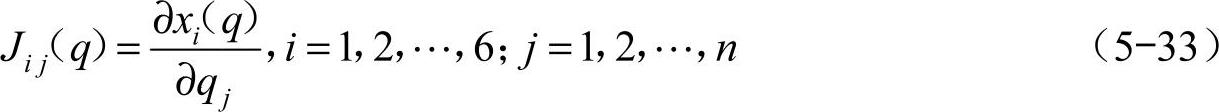(www.xing528.com)

仿生六足机器人腿部有3个关节，其雅可比矩阵J（q）是6×3阶矩阵，前3行代表足端线速度v的传动比，后3行代表足端角速度ω的传动比，所以足端速度可以表示为

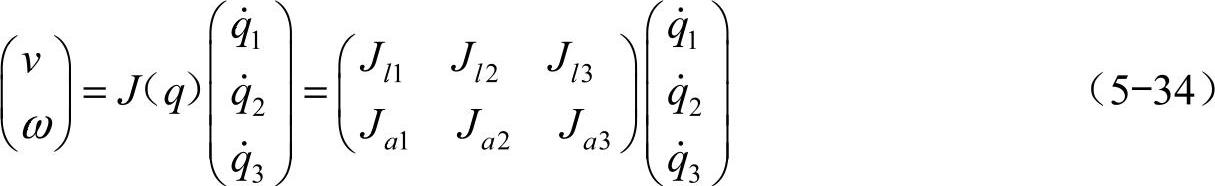
一般说来，我们需要的是机器人足端在空间的线速度，因此只求出线速度的雅可比矩阵

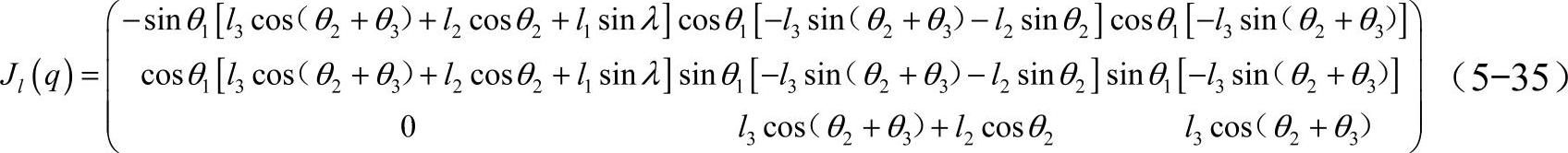
从式（5-35）可以看到，雅可比矩阵只与机器人的运动学尺寸、机构的类型及机构的位置有关，即与机构的位形有关。由此，可得出仿生六足机器人足端的线速度为

反之，已知机器人足端的线速度也能求得其转动关节的速度，以应用于机器人的控制，即有

（2）支撑相各腿速度分析 仿生六足机器人行走时，所形成的并联多环机构是由若干分支及中心平台组成的，可首先分析其中的一个分支，即一条腿的串联运动链。该串联运动链从足端到根关节包括了3个转动副和一个球副，其坐标系如图5-26所示。图中，各运动副轴线用单位矢量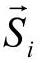表示；相邻轴线间公法线方向为单位矢量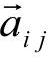，在相邻公法线间沿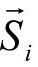的偏距为S_i，公法线长度为a_ij，转角为θ_j。这样机器人躯体的角速度ω_h可以表示为

式中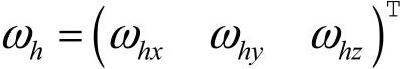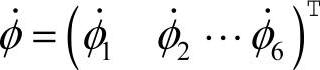，，为单分支中各个转角的速度，是机器人躯体转动对分支运动副变量的一阶偏导影响系数矩阵，且

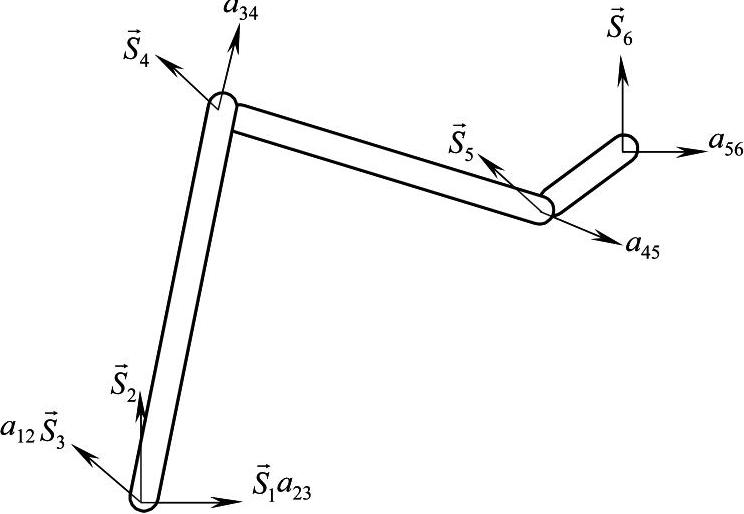
图5-26 单分支坐标系

机器人躯体上任一参考点P的线速度v_P可以表示为

式中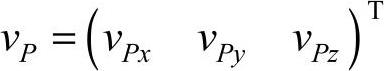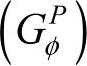，；是机器人躯体移动对分支运动副变量的一阶影响系数矩阵

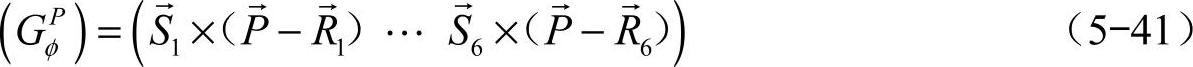
式中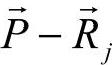，表示从第j坐标原点到p点的矢量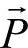，为躯体中心在基础坐标系中的位置矢量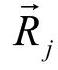，为j坐标系与基础坐标系两原点之间的距离矢量，且有

其中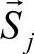、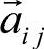根据初始条件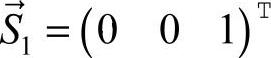和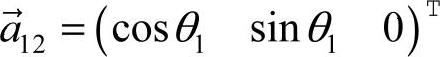，可由以下递推公式经计算得到，即已知

可有

和

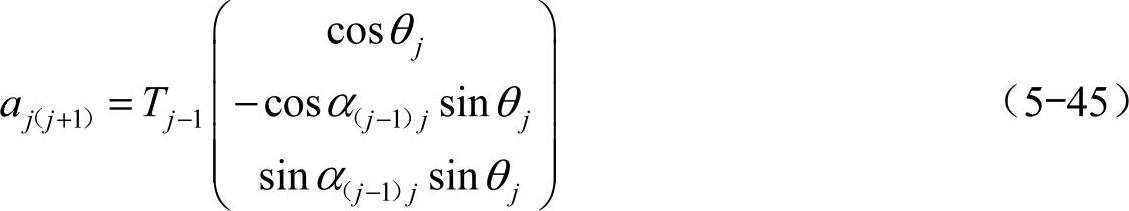
将式（5-38）和式（5-40）结合，可得综合公式

式中

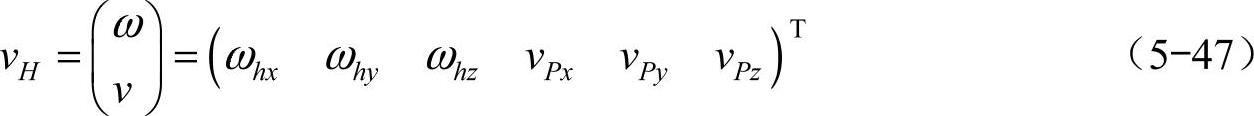
和

其中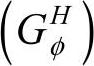是机器人躯体对分支的综合影响系数矩阵。当已知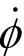求得v_H，为正解；而当已知v_H求得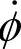，则为反解。

如前所述，当仿生六足机器人以“三角步态”行走时，为三分支并联机构。若已知机器人躯体的运动，则各分支中运动副的运动可以写为

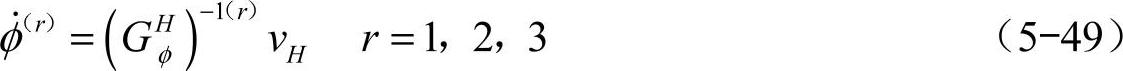
式中，r表示分支并联机构的分支序号，且并联机构上每个分支的影响系数矩阵与开链机构的形式相同。当确定了此6自由度机构的6个主动输入后，从式（5-49）中将6个主动运动的方程分别取出，可有

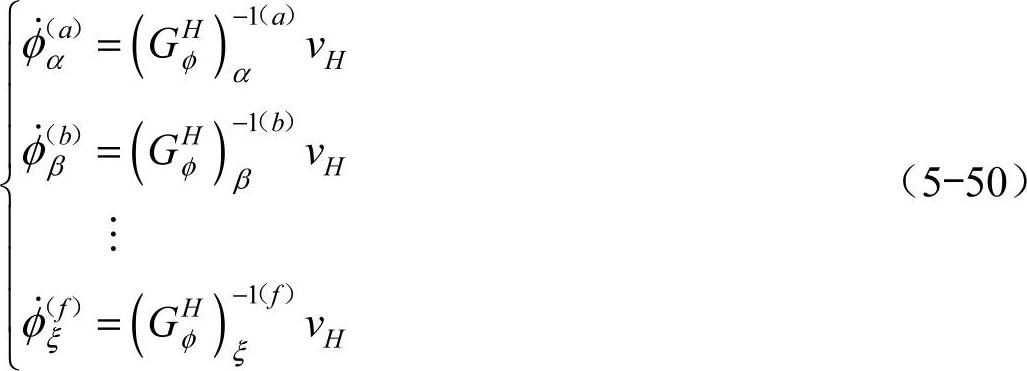
式中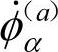，为输入角速度，其上角标和下角标分别表示输入角速度所在的分支序号和分支中运动副的序号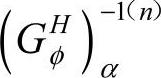；表示第a分支的逆矩阵的第α行。

将上述6个方程结合构成矩阵表达式，可有

式中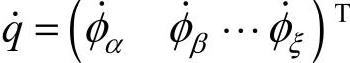，是独立广义坐标，且含6个输入角速度的列矢，而

于是可以得到逆解为

式（5-53）成立的条件是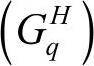为非奇异阵。应用式（5-51）和式（5-53），在已知6个广义输入速度的条件下，可以求得机器人躯体的六维速度，也可以由躯体的六维速度求6个广义输入速度。这里的一阶影响系数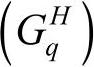是躯体运动对6个广义输入速度的综合影响系数，它同时与3个分支的18个运动副的方位有关，也与整个机构的位形有关。