昆虫观测实验：大学生科技创新竞赛获奖作品精析

1.实验对象的选择

本作品主要研究的是仿生六足机器人，设计的初衷是模拟六足纲昆虫的结构特征和性能特征，使所研制的机器人达到机动灵活、高效稳定和节能降耗的目的。因此，实验对象应该是六足纲昆虫。根据选择仿生观测实验对象应该遵循的几点原则：实验对象应与要研究的内容相符合、实验对象应具有典型性、实验对象应具有良好的可观察性和可分析性，选择蚂蚁作为实验对象。首先，蚂蚁是一种六足纲昆虫，种类繁多，分布广泛，易于采集，寿命较长，另外，蚂蚁的体积和爬行速度有利于采用高速摄像机进行实验数据的采集。最终选用日本弓背蚁作为仿生观测的实验对象，如图5-1所示。

2.实验平台的搭建

采用美国MotinXtra HG-TH 100K高速数字摄影机系统进行观察实验，如图5-2所示。该系统能同时将四路图像以最高1000f/s（frame per second）的速率采集并无损保存，多种拍摄触发方式有助于方便地捕捉事件瞬间变化的细节信息。为了保证在有限的曝光时间内获得较佳的影像数据，为该系统配备了多种光源：侧光光源离实验对象较远，采用大流明调焦柔光灯；背光光源靠近实验对象，采用发光二极管阵列提供均匀冷光；备有手持新闻灯随时补光。

恒湿、恒温的实验箱也是本实验的关键硬件之一，它是实验对象——蚂蚁的日常活动场所，也是观察蚂蚁行为的主要平台。不仅需要很好的透光性，而且要求较高的制作精度，以便进行精确的观测。所用的实验箱是用有机玻璃制作的长方体透明盒，尺寸为15mm×15mm×25mm。

实验布局示意图如图5-3所示。在相互垂直的三个轴向上各安置一个高速摄像头，而在三轴的交点处放置实验箱。在获得原始影像信息后，通过以下工作获得可供观测分析的数字数据。

1）对原始视频进行筛选、分类和整理。

2）使用视频编辑软件，完成所拍摄的三段视频信息的精确同步处理。

3）利用软件捕捉采集需求点的像素点坐标，完成模拟数据的数字化处理。

4）利用三视图两两之间的相互映射关系，校核并换算已获得的数字信息，得到可供分析的数据。

5）使用计算机进行实体模拟、仿真。

图5-1 实验对象——日本弓背蚁

图5-2 高速摄像机主要组件

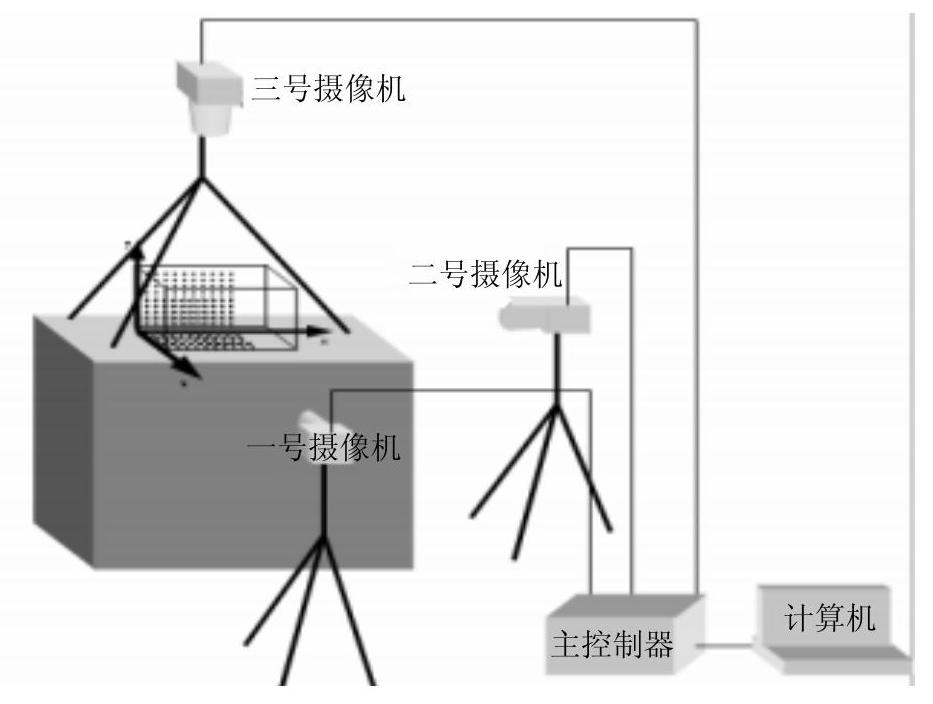
图5-3 实验布局示意图

3.弓背蚁运动特性观测实验研究

考虑蚂蚁的运动步态，匀速直行的步态无疑最具有代表性。本节重点探讨蚂蚁在匀速直行时的步态规律，然后研究蚂蚁在转向时的步态以作对比和参考。

采用如图5-4所示的方式对蚁足进行编号。通过观察发现，蚂蚁运动时，以足1、3、5为一组，以足2、4、6为另一组，以“三角形支架”结构交替前进，这和一般文献中所述的结论相同。然而，当蚂蚁直向前进时，其身体轴线与前进方向始终保持一致，并未出现一般文献中所述呈“之”字形曲线前进的现象。

图5-4 蚂蚁足序编号

典型样本中的蚂蚁体长约为11.5mm（不计蚂蚁触角长度），步距约为11mm，行走速度约为80mm/s。图5-5为蚂蚁样本连续行走两步的步态图，观察误差为±2ms，以足1触地时刻为起始时刻，以第二步摆动终止时刻为终止时刻，各段长度表示时间长短，段中的数字表示时间，单位为ms。

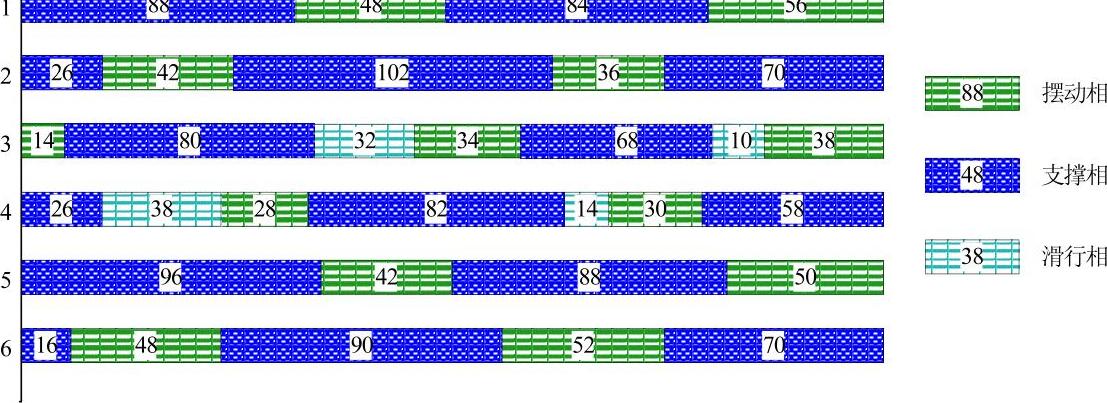
图5-5 蚂蚁样本连续行走两步的步态图

经观察发现，蚂蚁前足（1、6号足）、中足（2、5号足）触地时足端点固定不动，随后脱离地面迅速腾空，支撑相与摆动相区分明显，而蚂蚁后足（3、4号足）则不同，在足端触地时先保持足端点固定不动，然后贴着地面滑行一段距离，再脱离地面进入腾空阶段。

基于此发现，可以这样定义：蚁足触地但触地点不变的状态称为支撑相；完全腾空的状态称为摆动相；触地但触地点会有变化的状态称为滑行相。滑行相是支撑相与摆动相的边缘状态，既可以认为它是腾空运动而将其归为摆动相，也可以认为它能瞬间触地形成支撑而将其归为支撑相。蚂蚁在复杂地形中能很好地保持身体匀速平移及在高速运动中仍能以极大加速度起动、停止，这与滑行相的存在密不可分。

由图5-5可以看出：

1）任意时刻蚂蚁都至少有三只足着地，但仅有三只足着地的时间极其短暂，若将滑行相视为支撑相，则可以认为蚂蚁至少有四只足着地。

2）蚂蚁各足的有荷因数各不相同，不仅与相邻足不同，而且与对称足也不同，甚至前一周期与后一周期都有所不同。

3）蚂蚁中足的有荷因数最大，其次是前足，最小的是后足，但即使是后足，有何因数也都超过50%。

经过对大量实验结果的比较与分析，可以得到以下结论：

1）1、5号足（2、6号足）进入支撑相的时刻相同。

2）3、5号足（2、4号足）脱离支撑相的时刻相同。

3）1号足（6号足）脱离支撑相的时刻与4号足（3号足）进入支撑相的时刻相同。

假设在理想环境中以恒定速度前进的蚂蚁步态是绝对周期步态，各足的有荷因数不变，另外，对于蚂蚁的各足，与其相应对称的足有相同的有荷因数，步态为周期不规则步态（“不规则”表示各足的有荷因数不相同，与具有单一有荷因数的“规则”步态相对）。取{β₁，…，β₆，φ₁，…，φ₆}作为蚂蚁步态表达式，其中β_i，φ_i（i=1，2，…，6）分别为i号足的有荷因数和相对相位，则有

β₁=β₆，β₂=β₅，β₃=β₄ （5-1）

由结论1）可得

φ₁=φ₅，φ₂=φ₆ （5-2）

为简化推导，可令

φ₁=φ₅=0 （5-3）

同样由结论2）和3）可得

β₃+φ₃=φ₅，β₂+φ₂=β₄+φ₄ （5-4）

和

β₁=φ₄，β₆+φ₆=1+φ₃ （5-5）

由式（5-1）～式（5-5）可推导出蚂蚁的步态关系式如下

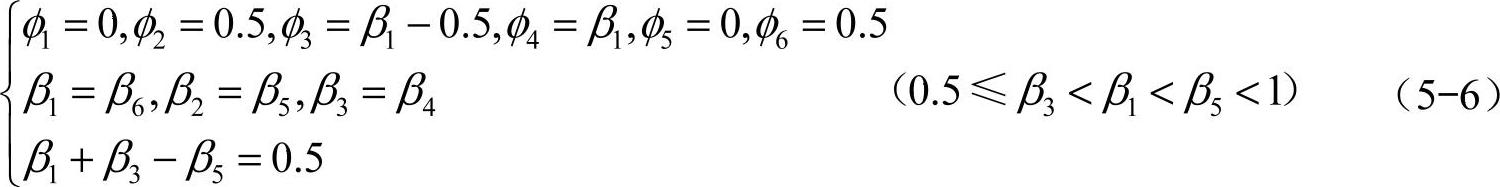
根据式（5-6）可知，一旦确定一组足的有荷因数（例如β₁，β₃，β₅）中的任意两个，即可得到蚂蚁的步态表达式。

上述样本中

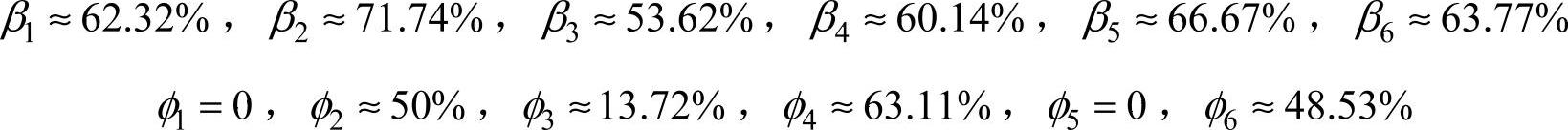(www.xing528.com)

所反映出来的情况基本印证了式（5-6）。

通过本实验可以发现：

1）早期的学者认为昆虫步态的有荷因数可以小于0.5，但本实验表明蚂蚁各足的有荷因数都不低于50%，国外对蟑螂等昆虫的研究也印证了这一结论。

2）蚂蚁的各足并非具有相同的有荷因数，而是处于周期不规则步态，各自的相对相位也不相同。与有荷因数大于50%的三角步态相比，不仅同样保证蚂蚁运动的稳定性，而且在相同条件下步行周期更短，从宏观来看，运动速度更高。

3）对蚂蚁步态的真实仿生并非如传统认识所认为的那么复杂。采用周期规则步态时只需确定一个有荷因数即可确定步态表达式，而采用周期不规则步态时，按照式（5-6）进行步态仿生也仅需要确定两个有荷因数即可。

当然，对蚂蚁步态进行真实仿生时，还可考虑如何实现蚂蚁后足的滑行相。经研究发现，蚂蚁后足的滑行时间虽然不恒定，但存在一定的规律：3号足（4号足）脱离滑动相进入摆动相的时刻早于5号足（2号足）脱离摆动相进入支撑相的时刻。其意义在于蚂蚁在1、5号足（6、2号足）即将无障碍地触地时3号足（4号足）已完全抬起，这样不仅能保证越障性能，同时还能提高移动速度。若定义γ为滑动时间与运动周期比，则有

0＜γ＜1−β₅ （5-7）

可以推断，若在仿生六足机器人的步态规划中按照式（5-7）加入滑动相，则非常有助于提高机器人的越障性能。

图5-6为以2号足摆动的初始时刻为起点连续记录两步的蚂蚁转向步态图，该图显示了蚂蚁样本经过两步完成一个转向的过程。由于蚂蚁在低速转向时后足基本上是在地面上滑动而不易区分滑动相和摆动相，所以在该图中将后足的滑动相视为摆动相。由图可见，蚂蚁在转向时速度大幅下降，与此同时，各足的有荷因数都有所增大，中足有荷因数的增幅尤其显著。因此，在仿生六足机器人的步态规划过程中，如果借鉴式（5-6）和式（5-7）反映出来的内在规律，在减小运动速度的同时提高各足的有荷因数，那么就能通过合理的足端轨迹规划，来获得与蚂蚁类似的转向特性。

依据前人的工作可知，多足机器人的运动规划问题可以转化为单足足端的轨迹规划问题。目前用于多足机器人足端轨迹规划的样本曲线以摆线、抛物线和正弦曲线等居多，这些曲线及其相应的轨迹规划方法各有利弊。此外，采用五次或六次多项式逼近的方法来解决多足机器人的运动规划问题，较前述方法更好，但美中不足的是，该方法是完全从数学角度出发推论而来的，缺乏现实依据，因而限制了它的实际应用。例如，该方法认为由给定的三点可唯一确定多足机器人单足足端的运动轨迹，然而如何给定这三点却并未探讨。因此研究蚂蚁的运动轨迹规律有着很高的学术价值。

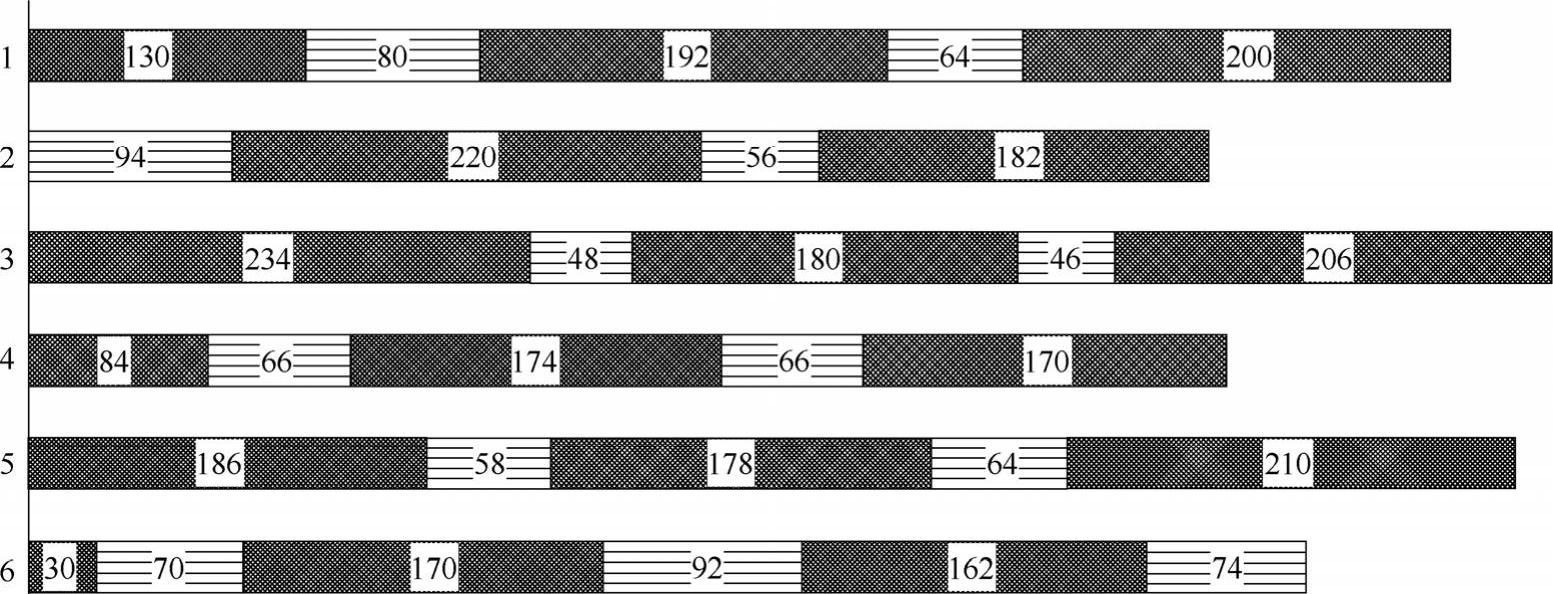
图5-6 蚂蚁转向步态图

图5-7为蚂蚁样本在两个步行周期内位姿变化的俯视图投影，其中不同颜色的彩色点分别对应224ms的观测实验时段内蚂蚁的头、尾顶点及足1～足6的端点在俯视图上的投影。若以垂直向上为x轴正方向，水平向左为y轴正方向，以右手定则确定z轴正方向，同时以蚂蚁头、尾顶点在t=0时刻的投影为坐标原点，即可绘制蚂蚁头、尾顶点轨迹沿各轴向的投影曲线，如图5-8所示。

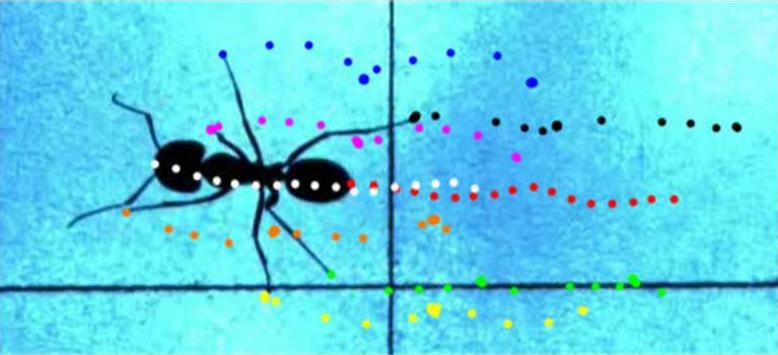
图5-7 蚂蚁头尾顶点及各足端点的俯视图投影

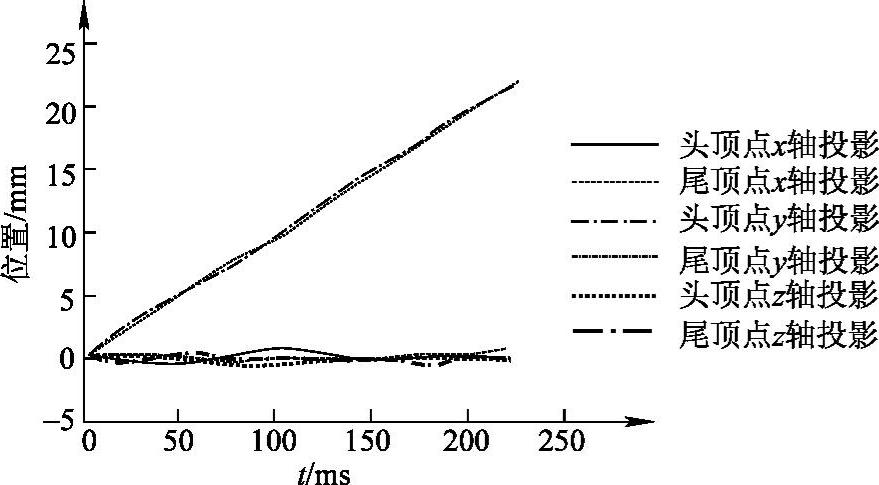
图5-8 蚂蚁头、尾顶点轨迹曲线

该蚂蚁样本的体长约为12.2mm（不计蚂蚁触角长度），步距约为10.2mm，行走速度约为87.6mm/s。若以蚂蚁头尾连线的中点为相对坐标系原点，则其头、尾顶点及足1～足6的端点在相对坐标系中的轨迹曲线如图5-9所示。

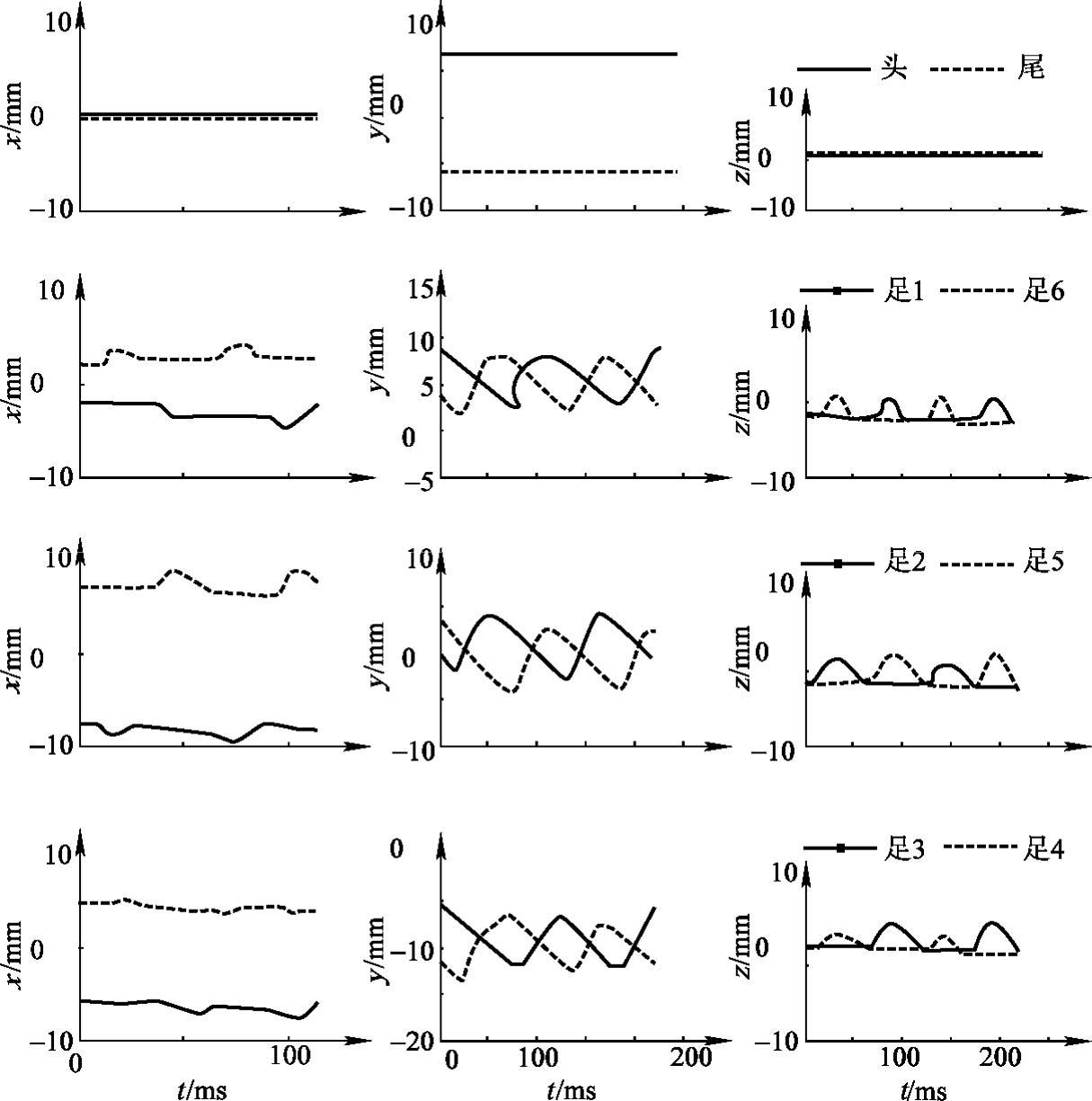
图5-9 蚂蚁头尾顶点及各足端点在相对坐标系中的轨迹曲线

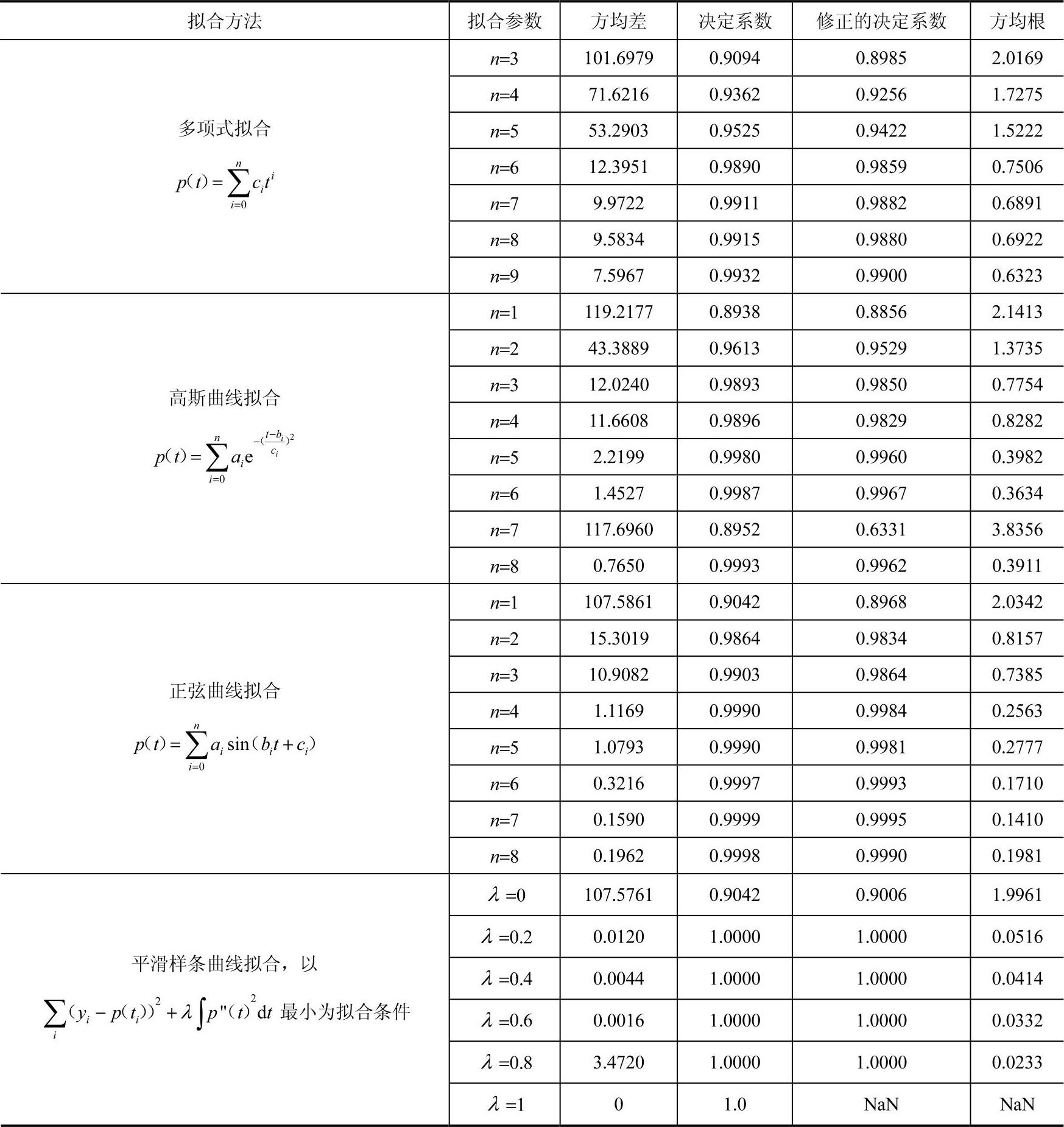
在对各点轨迹进行曲线拟合时，分别使用了多项式拟合、高斯曲线拟合、正弦曲线拟合、平滑样条拟合等拟合方法。以2号足为例，它沿y轴向的位移曲线的拟合效果如图5-10和表5-1所示。可以看出，平滑样条曲线拟合的效果最好，但是样条曲线仅具有拟合功能，不能有效地为具体实际需求规划轨迹曲线。多项式拟合、高斯曲线拟合及正弦曲线拟合，则能根据一定的条件来规划唯一轨迹。经过对比可以发现，这三种拟合方法的拟和质量都会随着阶数的升高而提高。另外，由三种曲线的拟合系数可以看出，由3n个已知条件可以唯一确定3n阶多项式曲线或者n阶高斯曲线或者n阶正弦曲线，而在拟合效果上，3n阶多项式曲线要远远好于n阶高斯曲线和n阶正弦曲线，所以多项式曲线是效果最理想的拟合曲线和规划曲线。由表5-1中多项式拟合结果的对比可知，六阶多项式曲线的拟合质量已经很高，更高阶的多项式曲线拟合对于拟合质量的提升已不明显，相应的计算量反而大幅增加。因此，采用六阶多项式曲线拟合蚂蚁足端的运动轨迹是较为合理的方法。

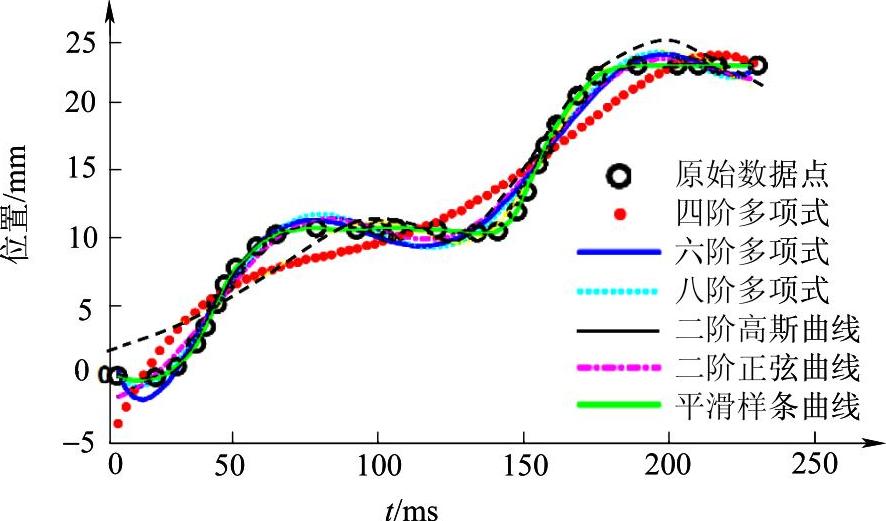
图5-10 2号足沿y轴向的位移拟合曲线

表5-12 号足沿y轴向位移曲线拟合方法及效果

由图5-8可以得出如下规律：蚂蚁在平坦路面上直线前进时，躯干的速度均匀，没有俯仰、倾覆或者旋转等现象出现。依据此规律，可将蚂蚁支撑相各足的足端运动视为匀速后退，这样可对蚂蚁支撑相各足的足端轨迹点进行线性拟合，而对摆动相各足采用六次多项式拟合，对应的拟合曲线为

式中，p（t）=[x（t），y（t），z（t）]^T表示随时间变化的足端轨迹矢量；c_i为多项式系数。

由图5-8和图5-9还可以得出如下另外三条规律：

1）蚂蚁各足歩距相同，并且每对对称足的落地点在y轴方向上均相差半个歩距。

2）处于同侧的前足与中足落地点的y轴坐标相同。

3）蚂蚁各足轨迹曲线的形状相同（后足在xOy平面上的轨迹投影近似为直线）。

根据规律3）选择蚂蚁的5号中足的轨迹做进一步分析，通过求导获得其速度、加速度的曲线如图5-11所示。由图5-11可见，速度和加速度的变化幅度都很小，曲线也相对平滑。

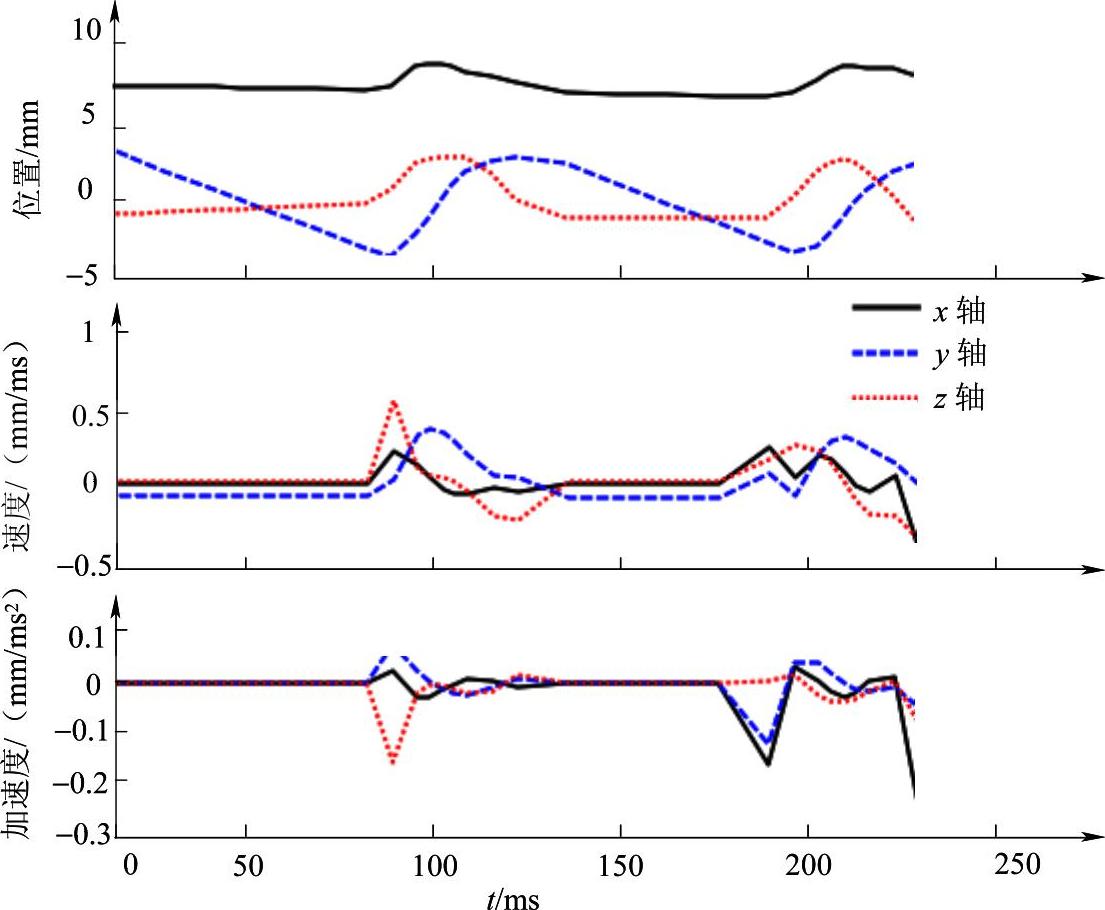
图5-11 中足足端位移、速度和加速度曲线

采用六阶多项式曲线进行足端轨迹规划，无疑没有高宽比、起角、落角等指标上的限制，可以根据具体环境规划出满足需求的曲线。根据对蚂蚁运动数据的统计与分析结果发现：蚂蚁在平坦路面上直线前进时，可采用六阶多项式拟合其足端轨迹，步距为躯体长度的85%，高宽比约为0.3:1，足端轨迹曲线所在的平面与水平面夹角为60º。

为了考察蚂蚁的越障性能，观测实验中模拟了两种障碍物情况----平铺障碍柱及堆叠障碍柱。蚂蚁的运动截图如图5-12～图5-15所示。图5-12显示了样本蚁沿障碍柱前进时的姿态；图5-13显示了样本蚁跨越障碍柱时的姿态；图5-14显示了样本蚁在障碍柱堆上前进时的姿态；图5-15则显示了样本蚁跨越障碍柱堆时的整个过程。

由上述四个典型样本可以发现，蚂蚁在应对两种障碍时，采取了不同的运动策略：

1）当面对高度小于其躯体离地高度的障碍柱时，蚂蚁始终保持躯体与地面平行，没有出现侧倾、俯仰或翻转的现象。

2）当面对高度大于其躯体离地高度的障碍柱堆时，蚂蚁调整位置和姿势以保持躯体与障碍物斜面平行。经过进一步的实验观察发现，几乎在任何时刻，蚂蚁的躯体都平行于支撑相核心三足所确定的平面（蚂蚁可能会有超过三只足处于支撑相，而此处的“核心”三足是指处于躯体一侧的前足、后足及对侧的中足），甚至当蚂蚁倒悬于障碍柱时也是如此。

这两种策略对于仿生六足机器人越障策略的设计具有重要的指导意义。

图5-12 蚂蚁沿障碍柱前进的三视图

图5-13 蚂蚁跨越障碍柱过程的主视图及俯视图

图5-14 蚂蚁在障碍柱堆上前进的主视图及俯视图

图5-15 蚂蚁跨越障碍柱堆过程的主视图