步态控制理论与技术—机械机电控制类获奖作品精析

运动足的自由度配置如图4-22所示。根据结构设计技术中对于机器人运动足结构尺寸设计，确定了运动足关键尺寸与各关节运动空间：根关节用于侧摆，摆动范围为[0°，135°]，基节l₁长为5mm；髋关节用于俯仰，俯仰范围为[-90°，45°]，股节l₂长为61.7mm；膝关节用于屈伸，屈伸范围为[0°，135°]，胫节l₃长为73.5mm；踝关节用于择向，选择范围为[0°，180°]，跟节l₄长为34mm。根据机械结构设计分析，并进行自由度抽象配置，可近似假设质心居于几何中点，根据具体参数对运动足建模如图4-23所示。

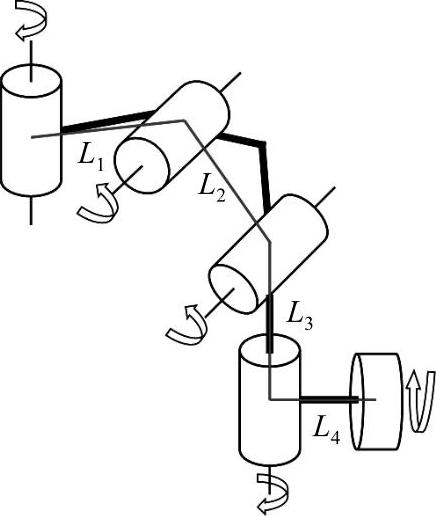
图4-22 运动足自由度简图

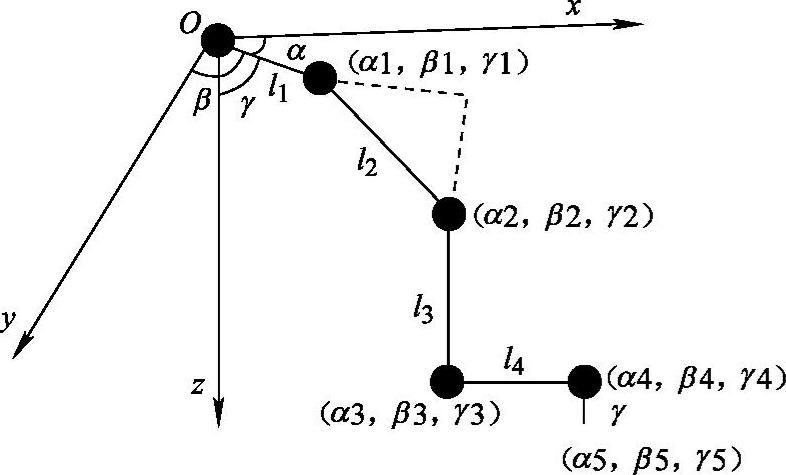
图4-23 运动足模型

根据各关节之间的距离l₁，l₂，l₃，l₄，r及各骨节与参考坐标系各轴之间的夹角α，β，γ，即可求得各转动关节在参考坐标系中的矩阵表达式。

第一个关节——根关节的坐标为（0，0，0），则其他四个关节及着地点在参考坐标系中的角度矩阵为

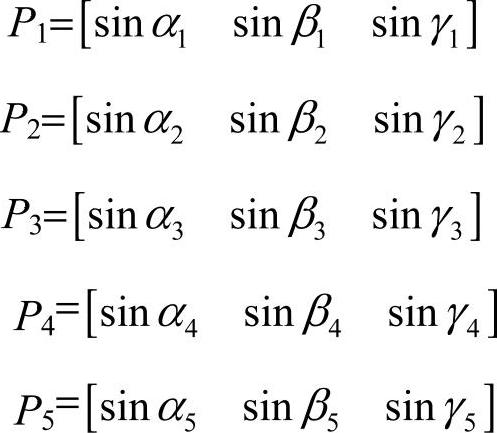
根据上述各关节及着地点的矩阵，可求的各关节点在参考坐标系中的位置坐标为

根关节：S₀=（0，0，0）

髋关节：S₁=S₀+l₁P₁

膝关节：S₂=S₁+l₂P₂

踝关节：S₃=S₂+l₃P₃

转轮轴：S₄=S₃+l₄P₄

着地点：S₅=S₄+rP₅

其中：l₁=5mm，l₂=61.7mm，l₃=73.5mm，l₄=34mm，r=35mm。根据上述各关节和着地点的坐标公式，即可得到当机器人运动时各关节点的坐标关系式，进行运动学正解和运动学反解运算，即可得到各关节点的控制角度，进而得到高精度直流伺服电动机和大角度精密转角舵机的控制量，对其进行精密控制，精确地实现所涉及的机器人运动步态控制。

1.运动学正解与运动学反解推导

（1）位置正解求法 运动学正解问题是给定各个关节处各骨节相对于参考坐标系的角度，求解运动腿着地点在参考坐标系中的位置坐标。采用数值解法从式中解出不同控制角度时落地点在参考坐标系中的坐标，计算结果见表4-4。(www.xing528.com)

表4-4 位置正解计算结果

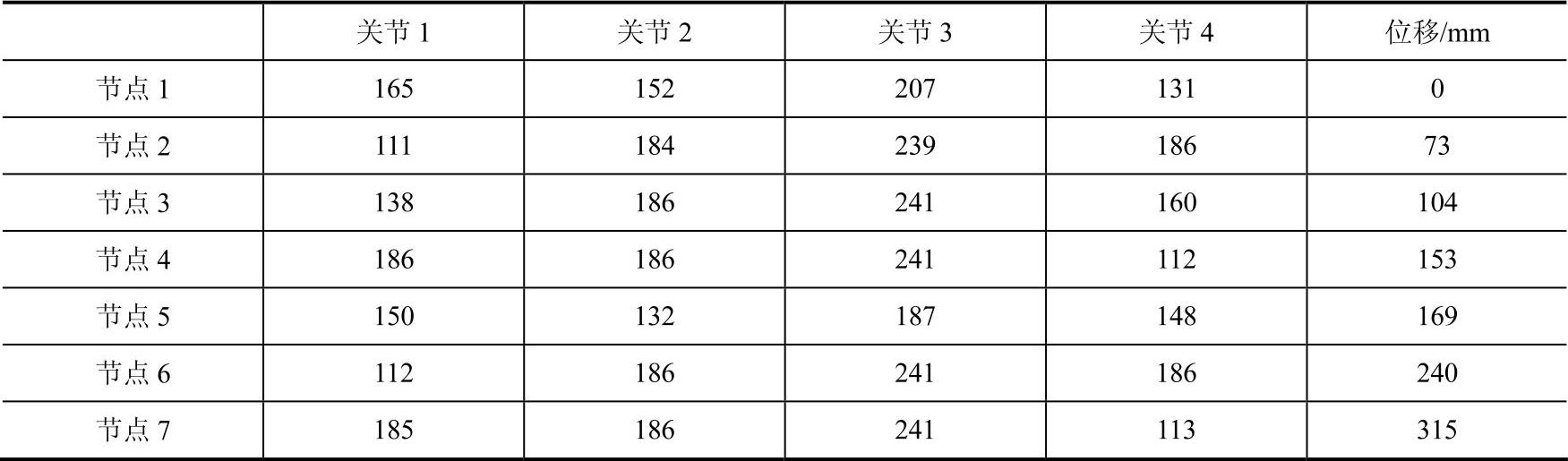
（2）位置反解求法 求解位置反解即给定机器人运动腿着地点在参考坐标系中的位置坐标，求解机器人每条运动腿上各关节处转动的角度，即各关节处舵机和直流伺服电动机的控制量。根据图4-23中运动腿的空间建模及各关节点的坐标公式可知，最终机器人的落地点坐标为

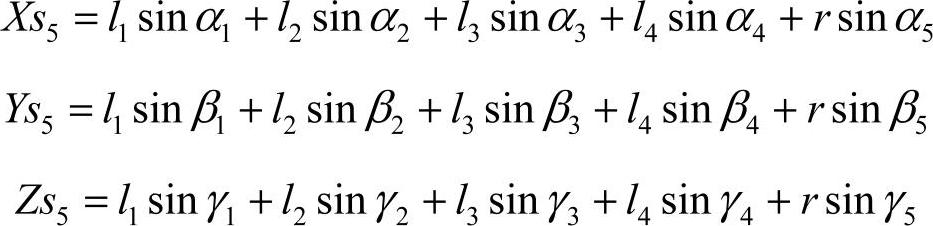
其中，Xs₅为运动时侧向位移；Ys₅为运动时前进的距离；Zs₅为运动时的机体离地高度。

根据以上分析可知，给定机器人的落地点位置后，应当逐次确定S₄、S₃、S₂和S₁，进而确定各关节处的控制角度。但各关节点的坐标之间相互关联，构成一组不定方程，因此方程的解并不是唯一确定的解，即相对于同一给定的着地点坐标，可由不定方程组解得多组控制量。因此通过位置反解求取控制量时，需要结合机器人各关节的运动角度范围和机械结构限制选择最优解。

经过运动正解和运动反解的严密推导，证明了机器人的运动腿能在其机械设计的可达域中自由控制。更进一步，为了使机器人的运动达到最佳效果，将运动正解和运动反解的解算结果作为机器人的控制量之前，应根据机器人的自身重量和运动地面的光滑度等因素对控制量进行适当的修正补偿。

2.步态多样性的探究

新型节肢机器人的功能展示性主要体现在其运行步态的多样性，其结合了抽象仿生学的相关设计原理，在结构和步态设计上，有机结合了昆虫爬行姿态和轮式机械行进的特点，在控制系统的统筹下分别设计了昆虫的多足爬行、螃蟹的横向侧行、仿人的腿式行走、蛇式的匍匐前进、机车的轮式滚动、履带式移动平台的原地旋转等多种行进步态。多足机器人的运动轨迹是一系列离散的足印运动，即只需要离散的点接触地面。其运动对环境的破坏程度较小，其足部可以在可能到达的地面上选择最优的支撑点，对崎岖地形的适应性强。在多足步行机器人的步行过程中，机器人的每条腿（足）根据一定的运动轨迹顺序提起和放下，因此可以把步态分解为摆动相与支撑相。以螃蟹横行步态为例，通过对该步态的实际观察结果可以得出螃蟹横行步态的时序图，如图4-24所示，黑色部分表示摆动相，白色表示支撑相）。图4-25为螃蟹足部标号设定。由此出发，将生物步态与机器人的仿生步态程序设计相结合，即可实现步态由生物体到机器人的移植转化。

在探索新型节肢机器人扩展步态时，通过对履带式移动平台的履带运动规律的观察、总结与推广，如履带式移动平台的原地旋转。对于履带式机器人而言，在实现原地旋转功能的时候，只需要保证两侧的履带以相同的转速与相反的转向进行运动即可实现。而对于如新型节肢机器人这种足部结构为轮腿结合式的机器人而言，运用足部末端舵机驱动的滚轮实现原地旋转功能时就必须进行特殊的步态设计。因为对于任何原地旋转的物体而言，其上任意一点均在其所在的一个与地面平行的平面内形成一个以某一点为中心的圆形轨迹。受此启发，结合新型节肢机器人的对称结构特性，如图4-26所示，将每条腿第四个关节处都旋转一个特定的角度以后，使得在机器人俯视图中每条腿末端横向直流有刷电动机旋转轴线的反向延长线交于一点O，且O点应该与俯视图中机器人的几何对称中心重合。然后，1、3、5、7足的末端滚轮与2、4、6、8足的末端滚轮分别以相同转速、相反转向转动，即可完美模拟履带式机器人的原地旋转功能。

图4-24 螃蟹横行步态的时序图

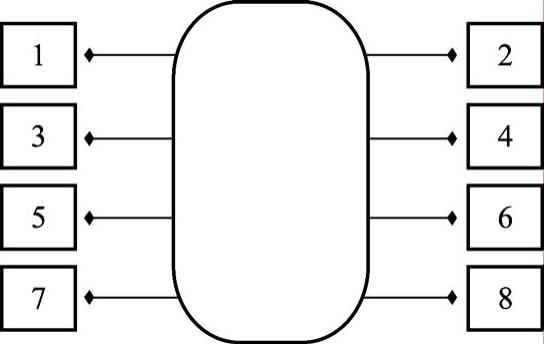
图4-25 螃蟹足部标号设定

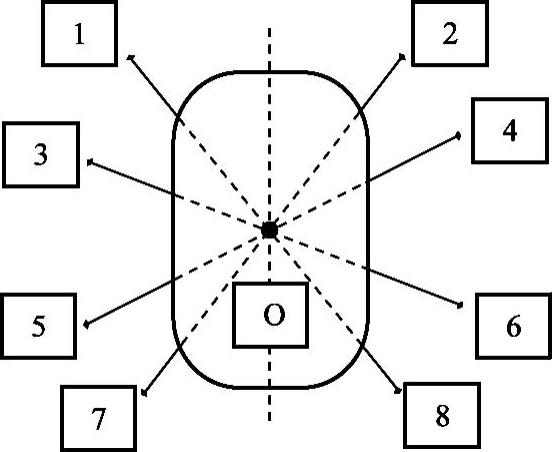
图4-26 原地旋转时机器人足部布局图