机器人步态分析：大学生科技竞赛获奖作品

1.三角步态的概念

从1877年迈布里奇用连续摄影方法研究动物的行走开始，人们对步行机构的步态进行了大量的研究工作，尤其是近二三十年来，关于步态研究的重要成果不断涌现。在20世纪60年代末，由于开发步行机器人的需要，Mc Ghee在总结前人对动物步态研究成果的基础上，比较系统地给出了关于步态的一系列描述方法和分析步态的严格数学定义，为步态的研究分析奠定了较为完整的数学基础。步态是步行机器人的一种迈步方式，是步行机器人各腿协调运行的规律，即各腿的抬腿和放腿顺序，它是研究步行机构的一个很重要的参数，是确保步行机构稳定运行的非常重要的因素。

“六足纲”昆虫（蟑螂、蚂蚁等）在平坦无阻的地面上快速行进时，多以交替的三角步态运动，即在步行时把六足分为两组，以身体一侧的前足、后足与另一侧的中足作为一组，形成一个稳定的三角架支撑身体，如图3-11所示。因此在同一时间内只有一组的三足起行走作用：前足用爪固定物体后拉动身体前进，中足用以支撑并举起所属一侧的身体，后足则推动身体前进，同时使身体转向，行走时身体向前并稍向外转，三足同时行动，然后再与另一组的三足交替进行，两组足如此交替地摆动和支撑，从而实现昆虫的快速运动，其行走的轨迹线是一条锯齿状曲线。

2.机器人起动步态分析

当新型轮腿式机器人从“卧”到“站”时，如图3-12所示，机器人的六条腿同时运转，带动机体克服重力做功。这时每个腿部驱动电动机所需转矩为

式中 G_max为机器人的最大重量，r为轮腿半径，h为电动机轴距箱底底部的距离。

从建立的数学模型推导可知，直形足部与弧形足部在电动机的驱动功率上近似，因此为计算方便起见，在这里及后续计算中不考虑弧形足部的问题，均采用直杆结构进行计算。

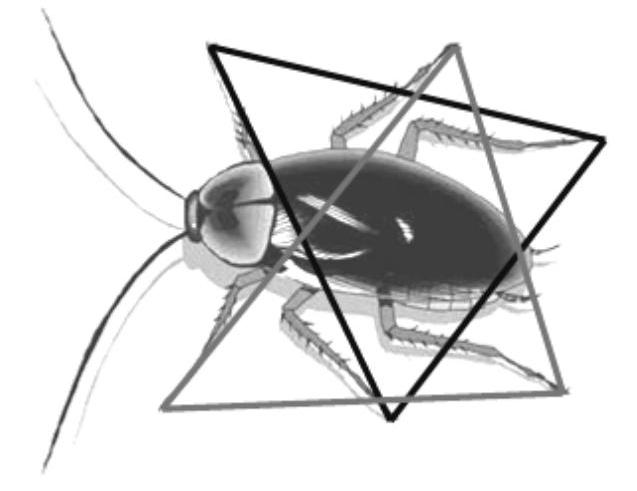
图3-11 蟑螂三角步态图

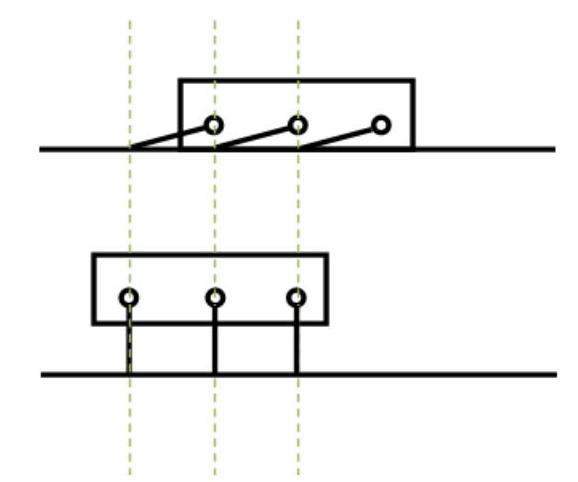
图3-12 新型轮腿式机器人从“卧”到“站”示意图

3.机器人直线行走步态分析

（1）慢速前进 如图3-13所示，当新型轮腿式机器人行进速度较慢时，机身始终保持有一组腿着地，此时机身重心成波浪形上下起伏，振动较大，但由于电动机在低转速时具有较大的转矩，因而可以借助腿部的支撑越过一定的垂直高度。由图3-13可知，腿每转90°时，机器人的跨步距离为

式中 r——轮腿的半径，这里为160mm。

而机体下降的高度为

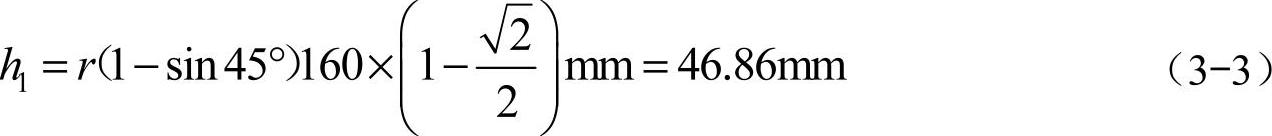
（2）快速前进 假设机体在整个运动过程中至少有一组腿着地，由前进速度v=3m/s，可得腿旋转的角速度为

腿的旋转周期为

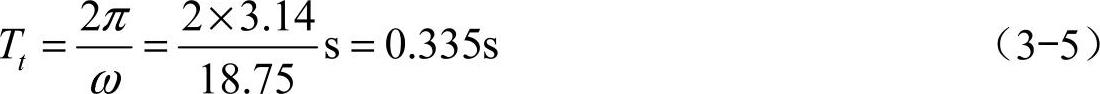
因此腿旋转45°所用的时间为

在竖直方向上，存在一个垂直加速度，则在竖直方向有(www.xing528.com)

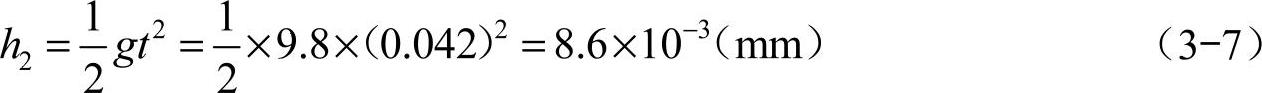
若要满足新型轮腿式机器人在整个运动过程中至少有一组腿着地，则需满足h₁=h₂，根据上述计算结果，显然等式是不成立的，h₂<<h₁，因此假设不成立，新型轮腿式机器人在快速前进时存在腾空阶段，在这段时间内，机器人做抛物运动，如图3-14所示，机器人具有类似于轮式机器人的快速移动能力。

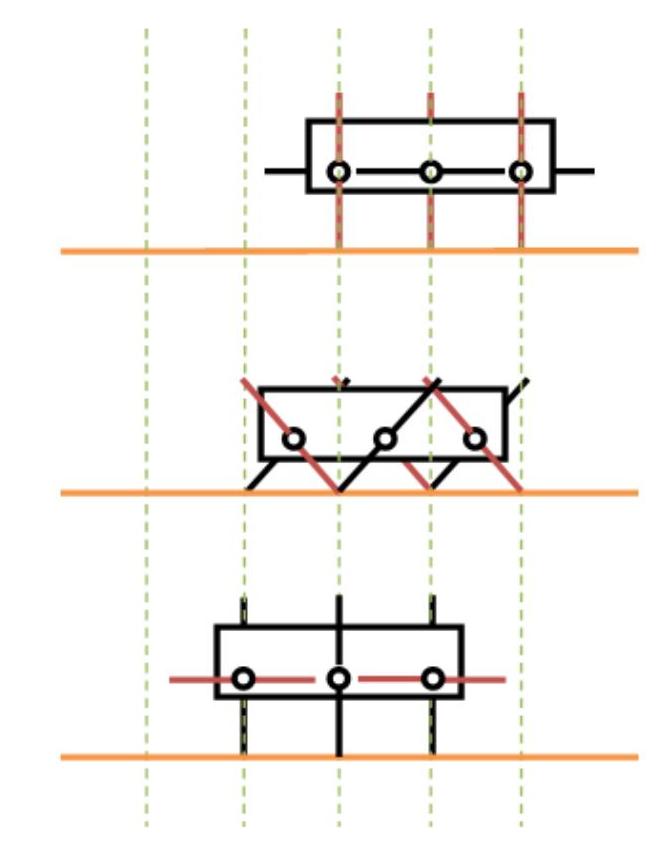
图3-13 机器人慢速前进示意图

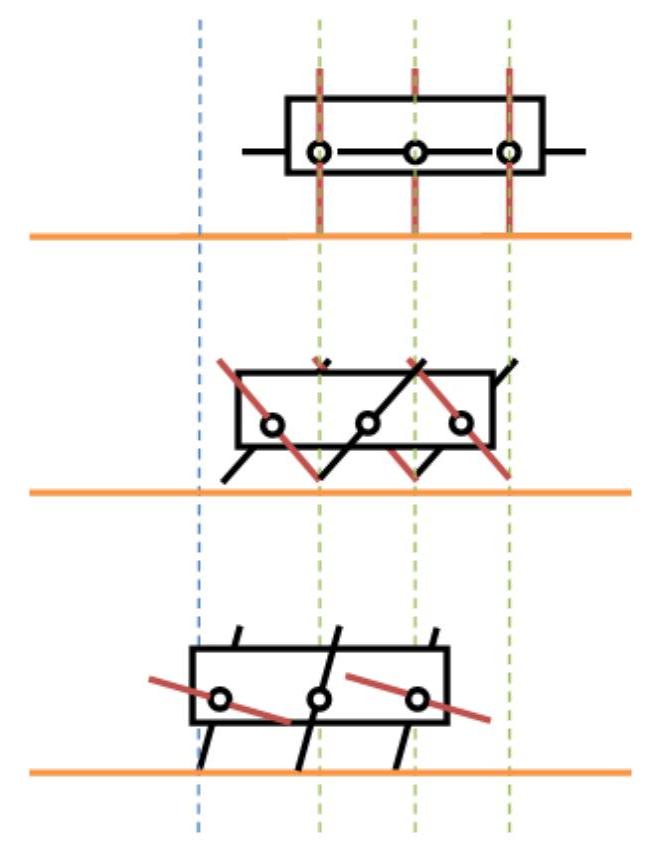
图3-14 机器人快速前进示意图

4.机器人转弯步态分析

（1）行进中转弯 对于在行进中的新型轮腿式机器人，要改变其运动方向，只需要调节各电动机的转速即可。机器人行进中转弯的示意图如图3-15所示。转弯时，将内侧电动机的转速降低，外侧电动机的转速增大，通过机器人内外两侧的速度差来实现转弯的功能。

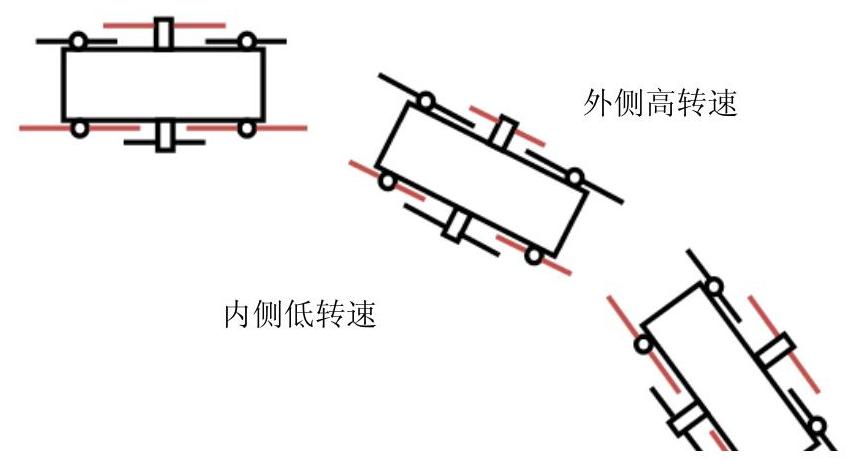
图3-15 机器人行进中转弯示意图

（2）原地转弯 首先对仿生六足机器人的原地转弯步态进行分析，不同步态时刻机器人各点位置矢量如图3-16所示。其运动步态具体为：

1）如图3-16a所示，机器人6条腿都着地，设为初始位置。

2）如图3-16b所示，机器人B₁、B₃腿旋转γ角度（设旋转γ角度后腿部在x轴上的投影长度近似为L）。

3）如图3-16c所示，机器人B组腿作支撑腿，A组腿抬起。

4）如图3-16d所示，机器人B组腿作支撑腿，A组腿抬起，做姿态调整。

5）如图3-16e所示，A组腿和B组腿均落地，作支撑腿，完成旋转γ角度动作。

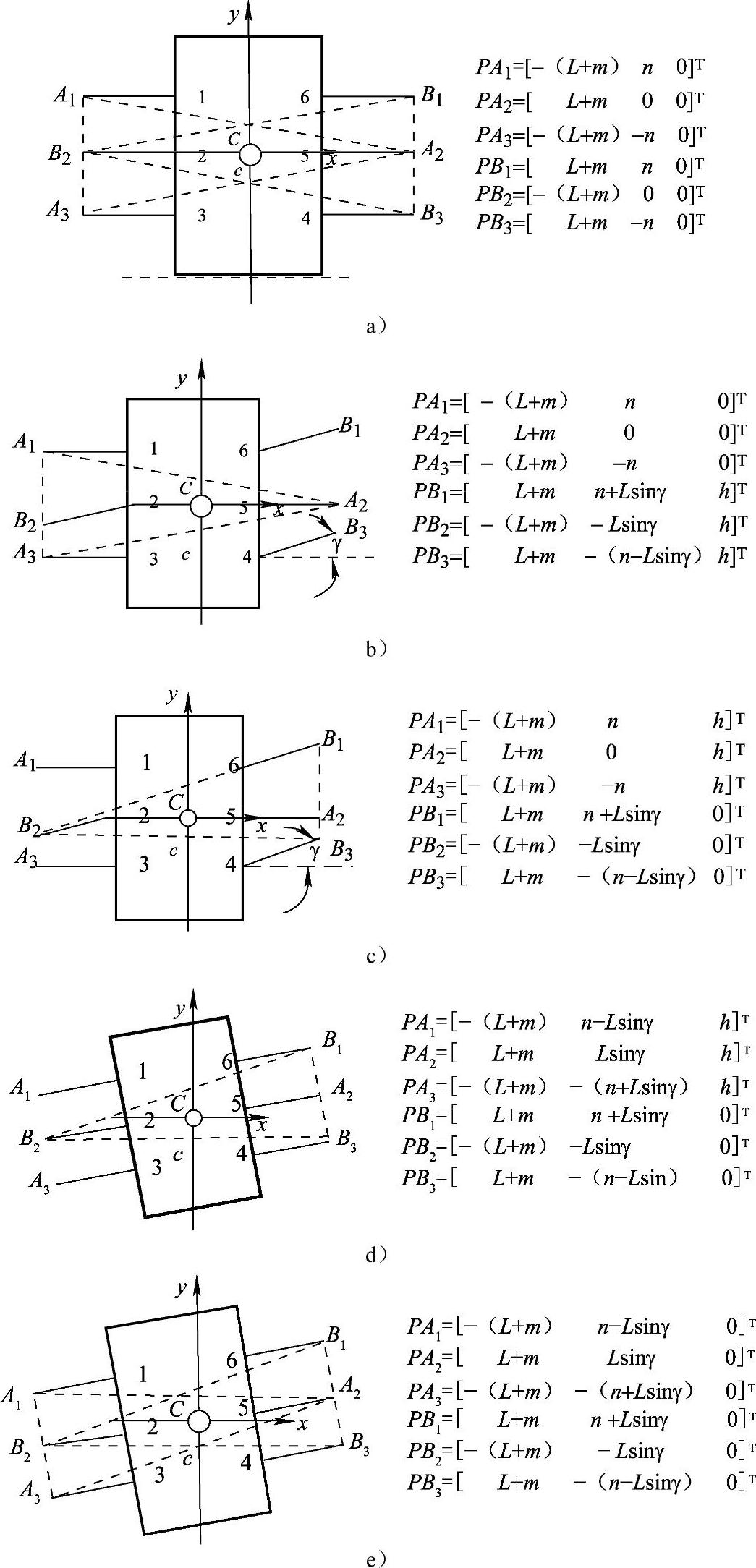
图3-16 六足机器人原地转弯步态图

新型轮腿式机器人的工作原理与仿生六足机器人大同小异，参照以上仿生六足机器人的原地转弯步态，下面分析新型轮腿式机器人的原地转弯步态。对新型轮腿式机器人的各腿进行编号，如图3-17所示。

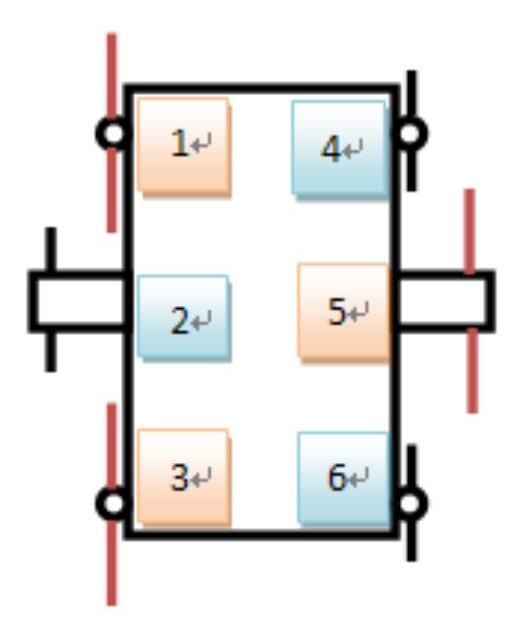
图3-17 新型轮腿式机器人各腿编号

机器人初始状态为六条腿均处于支撑相。以左转为例，假设A组腿（腿1、腿3、腿5）仍处于支撑状态，B组腿（腿2、腿4、推6）为摆动相。对于摆动相的腿，旋转方向内侧的电动机（腿2）反转，外侧的电动机（腿4、腿6）正转。当摆动相的腿（B组腿）快接触到地面时，支撑相的腿（A组腿）开始摆动，旋转方向内侧的电动机（腿1、腿3）反转，外侧的电动机（腿5）正转。在这个瞬间，完成支撑相（A组腿）与摆动相（B组腿）的互换，同时实现机器人的转向。当机器人右转时，则与上述情况刚好相反。

除了上述转弯方式之外，该机器人还能实现其他多种旋转变化。同样以左转为例，不过此时改为B组腿（腿2、腿4、腿6）为支撑相，A组腿（腿1、腿3、腿5）为摆动相。摆动的过程与上述过程相类似，唯一不同的就是所旋转的角度。另外，若机体最初处于“平躺”状态，要实现转弯的功能，机器人不必先站立起来进行类似上述的操作，完全可以在卧姿的状态下完成方向的改变。仍以左转为例，相对于旋转方向内侧的前腿（腿1）和中腿（腿2）反向旋转，剩下的腿（腿3、腿4、腿5、腿6）正向旋转，直到机体再次平躺在地上。这种旋转方式虽然电动机的负担比较大，但却能实现大角度的旋转。