政府(部门)作为委托人,把生产满足社会经济发展需要的职业教育产品的任务委托给政府企业——公立职业院校进行生产,并根据职业院校提供的职业教育产品数量和质量给予相应的拨款。代理人政府企业——公立职业院校通过自己的努力水平提供一定数量和质量的职业教育产品。委托人通过对代理人进行绩效评价,从两个方面监控代理人提供的职业教育产品数量和质量,一个方面是职业教育产品的产出和效果(如毕业生质量、技能成果、社会效果等),另一个方面就是职业院校的发展能力(如办学条件、专任教师情况、财务状况等)。政府(部门)通过考核这两个方面的绩效,来判断代理人的努力程度,并根据相应的努力程度给予一定的奖励或惩罚,以促使代理人提高绩效。
(一)委托人和代理人的相关假设
代理人为了完成委托人委托的任务,就要把努力(时间和精力)分配在两个产出结果上——职业教育产品产出效果s1和职业院校发展能力s2,其努力向量可以记为e=(e1,e2)T,其中e1是花在产出效果上的努力,e2是花在发展能力上的努力。我们假设:
s1=e1十θ1,s2=e2十θ2 (6-15)
其中,θ=(θ1,θ2)T,是正态分布随机变量,即E(θi)=0,Var(θi)=σi,Cov(θ1,θ2)=0。θi是完成第i项工作时工作环境的不确定因素,它可以表示对职业院校进行绩效评价时的误差,也可以表示成代理人在第i个工作上的努力而获得成功的风险。式(6-15)表示委托人所获得的职业教育产品数量和质量依赖于代理人的努力e和不确定性因素θ,这表明委托人和代理人关于代理人的行为信息是不对称的。
代理人付出努力e的成本函数为C(e1,e2),假设:
由于职业院校获得产出效果的任务与提高发展能力的任务是互补的,即一项工作努力程度的提高,会使另一项工作的追加成本降低,两种工作对知识技能的形成具有关联性。因此,有c12<0。
委托人采用线性激励函数方式给代理人支付预算资金,即代理人得到的预算资金为S(s1,s2)=a+b1s1+b2s2,其中a为代理人的固定预算,即保证职业院校生存的预算,b1和b2分别表示委托人根据产出效果和发展能力确定的拨款系数,相当于代理人对产出s1和s2的分享份额。
代理人的收益为得到的预算资金减去付出努力的货币价值:
其中下标a表示代理人。
委托人通过获得职业教育产出效果s1和职业院校发展能力s2而产生收益,用不变替代弹性函数(CES)表示委托人的收益:
其中,α表示产出效果s1对委托人效用的影响程度,1-α表示发展能力s2对委托人效用的影响程度,α可以根据绩效评价时的产出效果s1的权重来确定,0≤α≤1;γ是产出效果s1和发展能力s2的可替代弹性系数,因为s1和s2是互补的,所以γ∈(0,1);下标p表示委托人。
最后,我们假设委托人是风险中性的,代理人是风险规避的。
因为委托人风险中性,所以委托人的期望效用等于期望收益,即:
由于代理人是风险规避的,我们假设代理人的效用函数具有不变绝对风险规避特征,即代理人的效用函数为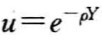 ,其中ρ为代理人的绝对风险规避度,Y为代理人的实际收益。如果u(Ya)=Eu(Ya),则称确定收益Ya为随机收益Ya的等价收益。代理人的等价收益可以用实际收益的期望值与风险成本之差来表达,代理人的风险成本为
,其中ρ为代理人的绝对风险规避度,Y为代理人的实际收益。如果u(Ya)=Eu(Ya),则称确定收益Ya为随机收益Ya的等价收益。代理人的等价收益可以用实际收益的期望值与风险成本之差来表达,代理人的风险成本为 ,即代理人宁愿在随机收益Ya中放弃
,即代理人宁愿在随机收益Ya中放弃
 的收益以换取确定性收益。因此,代理人的等价收益为:
的收益以换取确定性收益。因此,代理人的等价收益为:
(二)代理人和委托人的决策行为(https://www.xing528.com)
我们考虑一个代理人,他的有价值的努力水平向量e可以取两个可能的值,零努力水平的向量e=(e1,e2)=(0,0),正努力水平的向量e=(e1,e2)=(1,1),付出努力水平的成本函数为式(6-16)。代理人的生产过程具有随机性,随机的生产水平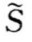 可以是两个向量{(s1,s2), (
可以是两个向量{(s1,s2), (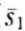 ,
,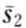 )}[4],努力对于生产的随机影响表现为概率分布Pr{
)}[4],努力对于生产的随机影响表现为概率分布Pr{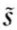 =
= |e=(0, 0)}=π0,Pr{
|e=(0, 0)}=π0,Pr{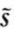 =
= |e=(1,1)}=π1,其中π1>π0。我们记△π=π1-π0为两个概率的差。
|e=(1,1)}=π1,其中π1>π0。我们记△π=π1-π0为两个概率的差。
注意努力在一阶随机占优的意义上提高产出,即,对任何给定的产出s*,Pr{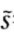 ≤s*|e}随e递减。我们有:
≤s*|e}随e递减。我们有:
以及
这一性质意味着委托人偏好于在正的努力水平e=(e1,e2)=(1. 1)条件下的随机生产分布,而不是无效的努力水平e=(e1,e2)=(0, 0),因为努力水平的增加会在很大程度上提高生产水平[5]。
代理人的行动不能被委托人直接观察到,委托人只能在可以观测到的和可验证的生产水平上提供一个契约,即一个将代理人的补偿同随机的产出联系起来的函数{b(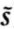 )}。因为有两个可能的产出向量s和
)}。因为有两个可能的产出向量s和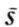 ,契约可以等价地定义为一对支付向量b和
,契约可以等价地定义为一对支付向量b和 [6]。
[6]。
风险中性的委托人的期望效用为:当代理人付出正的努力水平(e=(1,1)),则:
当代理人不付出任何努力时(e=(0,0)),则:
委托人希望激励出来的每一种努力水平,都对应着一个保证参与和激励相容的契约集。代理人的激励相容约束可以写成:
代理人的保留收益为Ya0>0,即代理人在没有政府拨款时通过社会服务等活动获得的最低收益。代理人要完成委托人的任务,获得的收益必须大于保留收益。所以代理人的参与约束可以写成:
当委托人要激励正的努力水平时,他的规划问题变成:
(三)模型求解
先将两个约束条件取等式,在构造拉格朗日函数为:
其中λ和μ分别为激励相容约束和参与约束的拉格朗日算子,对式(6-26)求一阶导数有:
求解式(6-27),得:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




