职业教育绩效评价与激励机制研究

（一）逐层“拉开档次”法的基本原理[1]

假设n个大系统S1，S2，S3，⋯作为被评价对象，设每个大系统Si都有p＝2个层次，且在各个层次中分别有Np（p＝2）个（相同级别的）子系统。现假定对第p层次（最底层次）的子系统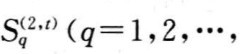 mt；t＝1，2，⋯，n1；m1＋m2＋⋯＋mn1＝n2）均取定mtq项评价指标（这里不妨都假定为定量指标）。

首先，对子系统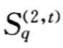进行综合评价。先将各项指标进行权化处理，即令：

（i＝1，2，⋯，n；j＝1，2，⋯，mtq；q＝1，2，⋯，mt；t＝1，2，⋯，n1）为权化指标，式中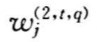）表示指标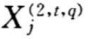）相对于评价目标的重要程度，称为权化系数。

分别令

第i个大系统关于子系统的综合评价值为

按“拉开档次法”求下面的线性规划问题的解，可以求得）确定权系数向量w的准则是能最大限度地体现出“质量”不同的系统之间的差异，也就是求指标向量x的线性函数w Tx，使此函数对n个系统取值的分散程度或方差尽可能地大。用数学语言表述就是求解如下线性规划问题：选择w，使得：

然后，对上一层子系统St（1）进行综合评价。先对y（2，t，q）进行权化处理，令：

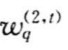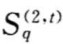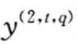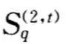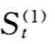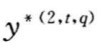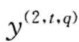式中是与（或）相对应的权化系数，其直观意义是表示子系统相会于母系统的重要程度。记为。令：

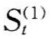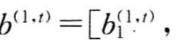
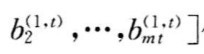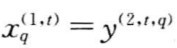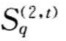为描述子系统运行状况的综合评价函数。式中仍为待定向量，为子系统的综合评价值。

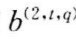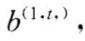仿求出将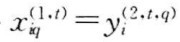代入上式，即得第i个大系统关于子系统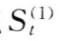的综合评价指标值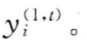

最后，对大系统S进行综合评价。在对y（1，t）进行权化处理后，令：

为描述系统S运行状况的综合评价函数。式中b＝（b1，b2，⋯， bn1）T仍为待定向量，而xt＝y（1，t）（t＝1，2，⋯，n）为子系统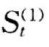的综合评价值。

仿b（1，t，）求出b，将x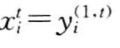代入上式，即得第i个大系统S 的综合评价指标值yi（i＝1，2，⋯，n）。

（二）用逐层“拉开档次”法对职业院校进行绩效评价

1.先求出三级指标的权化系数wj[2]

职业教育绩效评价指标体系共有12个二级指标和38个三级指标，按照逐层“拉开档次”法，首先要求出各三级指标相对于二级指标的权化系数。对于同一个二级指标下的三级指标，我们按照它们相对于二级指标的重要性，确定一个优先序。也就是说，若评价指标xi相对于某评价准则（或目标）的重要性程度大于（或不小于）xj时，则记为xi＞xj。通过对同一二级指标下所有三级指标进行两两比较后，可以确立一个序关系：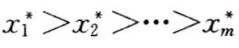

设评价指标xk－1与xk的重要性程度之比wk－1/wk的理性判断分别为：

wk－1/wk= rk,k= m ,m－ 1,m－2,⋯ ，3,2

当n较大时，可取rm＝1。

rk的赋值可参考表5-2。

表5-2

rk赋值参考表

若rk－1与rk满足rk－1＞1/rk，k＝m，m－1，m－2，⋯，3，2，则wm为：

根据上述原则，我们对每个二级指标下的三级指标进行重要性排序后，并对rk赋值，求得各个三级指标的权化系数wj如表5-3[3]。

表5-3职业教育绩效评价三级指标权化系数(www.xing528.com)

（续表）

2.用“规划求解”求得三级指标相对于二级指标的评价系数b（2，t，q）

首先将表5-1中的汇总数据分极大型、极小型和区间型等类型都进行极大化处理，再用极值处理法将各指标数值进行无量纲化处理，得到标准化的指标数据矩阵[4]。然后用表5-3中的权化系数wj乘以标准化数据矩阵，得到A（2，t，q）。

将矩阵A（2，t，q）的转置矩阵A（2，t，q）T与矩阵A（2，t，q）相乘，得H＝ATA，H 为实对称矩阵。再用Excel中的SUMPRODUCT 函数及其“工具”中的“规划求解”工具，可以求得各三级指标相对于它的二级指标的权重系数b（2，t，q），结果如下：

A1：A1＝0.228A11＋0.249A12＋0.171A14＋0.352A15

A2：A2＝0.56A21＋0.44A22

A3：A3＝A3

B1：B1＝0.147B11＋0.357B12＋0.227B13＋0.119B14＋0.149B15

B2：B2＝B21

B3：B3＝0.337B31＋0.530B32＋0.133B33

C1∶C1＝0.191C11＋0.200C12＋0.354C13＋0.256C14

C2∶C2＝0.467C21＋0.227C22＋0.306C23

C3∶C3＝0.287C31＋0.713C32

C4∶C4＝C42

C5∶C5＝0.180C51＋0.441C52＋0.298C53＋0.080C54

C6∶C6＝0.633C61＋0.367C62

3.依照上述方法求得二级指标对整个指标系统的评价系数b（1，t）

将各被评价院校的三级指标的无量纲化数据代入上述计算公式，得到各评价院校的二级指标数据矩阵，再进行无量纲化后，确定每个二级指标在相对应的一级指标中的权化系数wj。将权化系数乘以二级指标数据矩阵，得到A（1，t），再按H＝ATA求得H。同样用Excel中的“规划求解”工具计算出各二级指标相对一级指标的权重系数，并进行归一化处理。

4.计算各被评价院校的得分

为了减少确定权化系数过程中主观判断的影响，我们没有再用二级指标的评价系数对一级指标确定权重，而是用二级指标的评价系数b（1，t）进行归一化处理后，直接对整个系统确定权重系数，最后结果为

y＝0.067A1＋0.060A2＋0.206A3＋0.217B1＋0.034B2＋0.083B3＋0.046C1＋0.104C2＋0.045C3＋0.061C4＋0.043C5＋0.033C6

代入各职业院校二级指标数据矩阵中的数据，得到各试点被评价职业院校的得分（百分制）如表5-4。

表5-4 各职业院校最后得分

资料来源：专家评价分来自上海财大公共政策中心《2005年江苏省高等教育支出绩效评价报告》，2006年11月。专家来源：江苏省人大财经委、教科文卫委员会、省政协、省委政研室、省府政研室等。