在上一节的讨论中，我们忽略了一个问题，即物体的重力会随着物体与地面距离的增大而减小。其实，万有引力就是我们口中的重力。根据牛顿定律，两个物体间的引力与它们之间距离的平方成反比。就是说，两个物体间的引力会随着距离的增大而减小。在计算重力时，我们总是习惯性地把地心当作地球质量的集中点，地球和物体之间的距离就是地心到物体的距离，等于物体与地面的距离和地球半径之和。6400千米高空，相当于地球半径的2倍，地球引力是地球表面引力的
。
如果把这一规律用于竖直向上发射的炮弹，由于炮弹在高空时受到重力的影响较小，它上升的高度明显比不考虑重力影响的情况大。假设炮弹的初速度为8000米／秒，如果考虑重力随高度变化的因素，炮弹能够达到的最大高度应该为6400千米，但如果对这个因素忽略不计，直接套用公式，得到的结果仅为该数值的一半。对此，我们可以通过下面的计算来进行验证。在物理学和力学中，假如一个物体竖直上升的初速度为v，重力加速度g不变，可以用以下公式来计算出它达到的最大高度：
其中，v=8000米／秒，g=9.8米／秒2。
即：
可见，该数值差不多是地球半径（6400千米）的一半。此时忽略了重力随高度变化的影响，所以产生的误差非常大。炮弹升得越高，地球与炮弹之间的引力就越小，而炮弹的初速度保持不变，所以此时炮弹会升到更高的 位置。
要说明的是，我们没有怀疑传统物理公式的正确性的想法，在公式的适用范围内，它仍然是适用的。一般来说，在物体与地面离得不太远的前提下，完全可以忽略重力减小的影响。比方说，一个物体竖直上升的初速度是300米／秒，在该过程中，它的重力减小得并不明显，可以忽略不计，所以完全可以用上述公式来进行计算。
根据这一规律，如果火箭或飞船升到高空，在离地球非常远的地方，重力是不是会变得很小呢？也可以这样说，一个物体在非常高的空中，质量会发生什么样的变化呢？1936年，一位叫康斯坦丁·康基纳奇的飞行家特意对此进行了实验。当时，这位飞行家做了三次试验，每次带的物体都不一样重，这样便可以知道当物体达到一定高度时，它的质量会发生什么样的变化。第一次，他带着0.5吨的物体升到了11458米的高空。第二次，他带着1吨的物体升到了12100米的高空。第三次，他带着2吨的物体抵达了11295米的高空。实验结果怎样呢？有的读者或许认为，地球的半径是6400千米，仅仅是在该基础上增加了12千米，变化很小，对质量的影响小到可以忽略不计。但实际结果却让我们大吃一惊，距离只增加了一点儿，物体的质量却轻了很多。
下面，就来具体分析一下第三次实验：物体在地面时的质量为2吨，飞在11295米的高空，相当于地面上的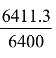
（分数写法）倍，因此物体在空中和地面所受到的引力之比为：(www.xing528.com)
所以，在11295米高空，物体的质量为：
利用近似值算法，得到的结果是1993千克。这意味着，2吨重的物体升高到11.3千米的高空后，质量会减少7千克！如果换成1千克重的砝码，则在该高度，它的质量会减少为996.5克。
事实上，此类例子数不胜数：俄国的一艘平流层飞艇飞到22千米的高空时，发现每千克质量减少了7克。同样，1936年，飞行员尤马舍夫携带5000千克重的物体飞到8919米的高空时，物体的质量减少了14千克。
依据上述方法，我们可以来分析一下下面两种情况：
（1）1936年11月4日，飞行员阿列克谢耶夫携带1吨重的物体飞到12695米的高空时，物体质量的变化情况如何？
（2）1936年11月11日，飞行员纽赫季科夫携带10吨重的物体飞到7032米的高空时，物体质量的变化情况又如何？
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
