车内低频噪声的计算一般是利用有限元方法实现的。将车内空腔划分网格,建立有限元模型,再与车身结构的有限元模型相耦合,通过流体(空气)与结构之间的相互作用(Fluid Structure Interaction,FSI),将结构振动与空腔声场联系起来,建立FSI模型(也称声固耦合模型),从而可以计算车室空腔的声学特性,以及由结构振动产生的车内噪声响应。
对于中高频(300Hz以上)噪声特性的仿真分析,如果采用有限元方法建立模型,则会大大增加工作量并且其准确程度并不高,因此应采用建立在空间声学和统计力学基础上的统计能量分析(Statistical Energy Analysis,SEA)方法。实践证明,利用SEA模型分析汽车在250Hz以上的噪声特性能够得到令人满意的结果。
(1)声固耦合分析法。建立车室声固耦合模型时,车身结构模型和车室空腔声学模型是利用有限元前处理程序提供的壳单元和三维实体(六面体等)单元分别建立的。如图8-3所示是某轿车的车身结构有限元模型,如图8-4所示是根据结构模型建立的车室空腔有限元模型。

图8-4 轿车车室空腔有限元模型

图8-3 轿车车身结构有限元模型(右侧一半)
为了与车身结构模型相耦合,空腔表面的节点必须与车身结构的节点全部重合,并且在模型数据文件中定义两个模型中相重合的节点连接(耦合)在一起,保证它们在分析时运动,这就完成了声固耦合系统模型,如图8-5所示。
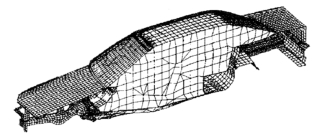
图8-5 车室声固耦合系统模型
车室空腔系统的声学特征表现为与固有频率和振型(声压分布)相联系的声学振动模态。强迫振动下车室内部各点的总压力响应取决于各声学模态被激励的方式,车室空腔的共振会明显增大噪声响应。掌握车内空腔的声学模态频率和模态振型,可以在设计过程中避免车身结构振动导致的车内共鸣噪声,合理布置和优化车内声学特性,尽量使人耳处于最重要声学模态的节线位置,从而获得较好的舒适性。对声固耦合系统进行模态分析,可以识别出系统的模态频率和振型,为预测并分析声学响应准备必要的条件。
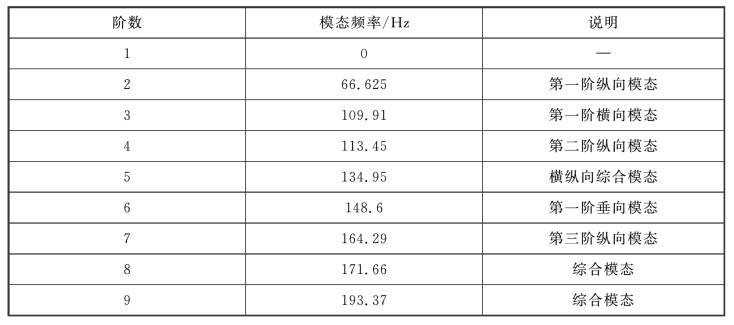
利用Nastran软件对车室空腔声学模型(见图8-4)进行模态分析,计算出的模态频率结果见表8-1。第一阶模态的频率为0,相应的振型中车室内各点声压变化的幅值相同,相当于结构模态中的刚体模态。车室空腔系统的声学模态(车室内的声压分布情况)如图8-6所示。图中黑色区域的相对声压最小,近似为零,相当于节线(声压为零的界线)区域。模型中不同的颜色代表着不同的相对声压,它们的大小由图中右侧的色带表示,越往上的颜色表示声压的相对变化量越大。由图可知,第一阶纵向声学模态(见图8-6a)的节线大致处于车室的中间位置,向两端声压逐渐增大。由于车室空腔模型是左右对称的,因此室内声压分布也是对称的。图8-6(b)中的声压是横向分布的,节线处于车室的纵向对称面上。图8-6(c)的声学模态表现为声压在横、纵两个方向上分布的综合模式,它的节线近似为首阶横、纵向模态节线相叠加的结果。另外,因车室形状在垂直方向上很不规则,导致垂向模态(见图8-6d)的声压分布也不规则,且节线变得不清晰。

图8-6 车室空腔的声学模态
表8-1 车室空腔的声学模态频率(200Hz以内)
空腔声学模态是通过边界条件与车身结构的振动相耦合的,这种边界条件(开放的、刚性的或弹性的)建立了车室内声压的变化与车身壁板振动之间的关系,因此空腔声学特性和车身结构动力学特性共同决定了车室内部的声压。试验表明:车身壁板的振动会改动声学模态的频率,移动节线的位置,并使车室内的噪声响应发生重大变化。
由于耦合系统是由结构和空腔相互作用形成的,因此它的模态与结构和空腔两个系统的模态基本是对应的。耦合系统的模态振型由两部分组成:结构的变形和空腔流体中声压的分布。这些模态可能是结构振动引起的声压分布变化(结构变形占主要地位),也可能是声压变化引起的结构振动所产生的(即声压变化为主),它们分别对应着结构和空腔两个系统各自的模态。(https://www.xing528.com)
如图8-7所示耦合系统模态是以车身结构变形为主的模态。车身结构的振动(见图8-7a)使空腔流体的声压发生变化,产生图8-7(b)中的振动模式。与车身结构系统相应的模态相比较,耦合系统的模态频率稍有变化,但变化量很小,而车身结构的变形部位基本没有变化。图8-8所示为以流体声压变化为主的耦合系统模态,结构因流体的振动(见图8-8a)而产生变形,如图8-8(b)所示。它对应着空腔系统的第一阶纵向声学模态。结构壁板的振动使耦合系统中空腔流体的振动模态(空腔内声压的分布情况)出现了变化。与空腔系统声学模态相比,模态频率变化较小,而模态振型变得更加不规则,节线略微前移,前部声压的相对变化更大了。
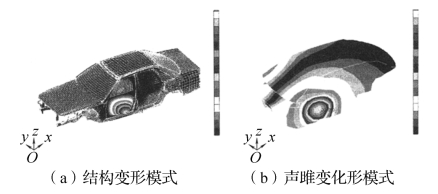
图8-7 结构变形为主的耦合系统模态中流体的变形模式

图8-8 流体变形为主的耦合系统模态中结构的变形模式(66.111Hz)
车室内部噪声的预测是汽车NVH特性研究的重要内容。与耦合系统的模态分析相比,计算车身壁板振动引起的车室噪声可以获得更直接、更实际的NVH特性,更有利于将NVH目标与系统特性相联系,以便进行NVH目标的分级与评价。将整车刚弹耦合模型分析得到的车身连接点处的力作用在声固耦合模型中相应的结构节点处,就可以进行响应分析。
(2)统计能量分析法。统计能量分析方法是利用所研究对象各子系统之间具有统计意义的能量参量的变化,来研究其动力学特性的方法。它对于求解高频区模态十分密集的复杂系统的动力学问题非常有效。
由于系统受到的激励是随机变化的,响应也是随机变化的,因此要用统计学的理论对各子系统总体能量的统计特性进行分析。用能量来描述动力学子系统的状态,用功率的流动平衡方程描述耦合子系统间的相互作用,这样就可以将“能量”作为独立的动力学变量来解决结构、声场间的耦合动力学问题。
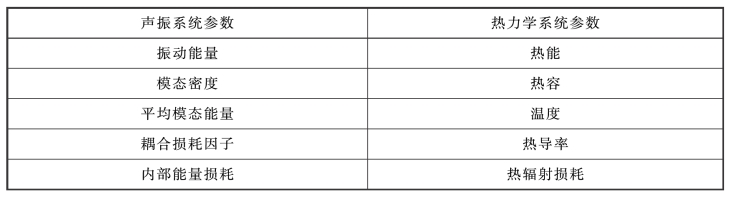
声振子系统之间振动能量的传递关系类似于热力学中热能的传递关系。在热力学问题中,热能从高温载体流向低温载体,载体中储存热能的多少取决于其热容,两载体之间的热流量正比于它们的温度差,此比例常数就是热导率。此外,两个载体都存在向外的热辐射损耗。声振系统中的振动能量类似于热能,子系统的模态密度类似于热力学中的热容,而子系统的平均模态能量类似于热力学中的温度。声振系统的能量损耗(由阻尼消耗)类似于热力学中的热辐射损耗,其损耗能量的多少用内损耗因子来衡量。声振子系统间的耦合损耗因子,是用来描述耦合系统之间耦合强度的量纲为一的物理量,它是统计能量分析中的一个重要参数,类似于热力学中的热导率,见表8-2。
表8-2 声振系统与热力学系统参数的类比
由于统计能量分析方法中的“能量”依赖于子系统的模态密度,即单位频带宽度内模态数量的多少,因此系统模态密度的大小直接影响到它的准确程度。统计能量分析适用于解决高频区(单位带宽内的振型数N≥5)的复杂动力学问题,而模态法和有限元法则适用于解决低频问题(N≤1)。
统计能量分析的估计精度一般随系统模型的细化而提高,但由于统计能量分析给出的是空间和频域的平均量,因此得不到系统内特殊位置上和特殊频率处响应的详细信息,即它不能预测子系统内某个局部位置的精确响应,但能较精确地从统计意义上预示整个子系统的响应级。例如:对于车室空腔声学子系统,它可以预测出车内的平均声压级,但不能给出驾驶人耳旁位置处的声压响应信号。这是统计能量分析方法的局限性之一。
在统计能量分析的理论中,一些基本关系方程都是在保守、弱耦合以及激励源不相关等假设条件下建立的,并且在数学上也不是很严密的。这样,在实际结构与理想系统相差较大时,就会给预测结果带来较大偏差。例如:在实际结构中,子系统之间的边界连接(如螺纹连接、焊接、销接和铰接等)是具有耦合阻尼的,这种阻尼不能被忽略,但它们对内损耗因子、耦合损耗因子的不同影响还不能从理论上区分开。此外,将统计能量分析方法推广到强耦合系统以及相关激励作用下的系统,都是需要进一步解决的问题。
在统计能量分析中,一般都假定模态参数是按泊松过程分布的,但这一假设对复杂系统并不成立,这将对预测能量响应的方差产生很大影响,从而制约了它在中、低频范围内的应用。
应用统计能量分析解决工程动力学问题时,可分为以下三个步骤:①分析实际系统的结构,划分子系统并建立SEA模型;②确定各子系统以及它们之间的统计能量分析参数,并计算各子系统的振动能量;③估算各子系统的动力响应。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




