汽车车身设计-分割与比例技巧

汽车造型设计，要从主体的角度去设计汽车的形体，也要从理性和情感的角度去认识和理解汽车这个实体与空间的关系。造型设计往往是在三维空间内进行的。形体与空间的分割或区分必然涉及一些比例方面的知识，正如意大利艺术大师达·芬奇所说：“美感应完全站立在各部分之间神圣的比例关系之上。”对汽车而言，只有在三维空间中具有均衡的比例，才能使其造型获得整体感。

在汽车造型中经常碰到的比例关系有整数比例（如1∶1、1∶5、1∶2等）、平方根比例（如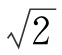1∶、1∶等）和黄金分割比例。

整数比例关系在自然界中和人们的生活实践中都很常见。

1∶（1∶1.1414）是正方形的一边与其对角线的比例，也存在于等腰直角三角形中，即是书、报、纸张用的比例。1∶（1∶1.732）的比例存在于等边三角形中，也是矩形的一边与其对角线的比例。如图4-1所示，这些比例关系在机械零件、建筑物、力学桁架及许多艺术品中已获得运用。

图4-1 根号矩形作图法

1.黄金分割比例

黄金分割是古典装饰理论中划分已知线段成两段的最佳方法。因为该分割比例能产生既多样又统一的效果，如图4-2中将A 1C 1用B 1等分，或将A 2C 2用B 2来划分，前者造成了等强分，后者造成了过强的对比，因此都是不理想的划分方法。黄金分割的多样性是由AB与BC的长度差别而获得的，其统一性则是由于AB与BC的长度又互相接近，而且形成了比例的重复。通过列方程求解可知，当BC＞AB时，黄金分割的比值为1.168；当BC＜AB时，其黄金分割的比值为0.618。因此，AB/BC=BC/AC=1/1.168=0.618。这个比值是无理数，极难计算数字，但在几何学上却是简单求得优美的比例。

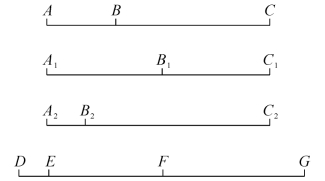
图4-2 线段的划分

2.黄金分割的几何学作图

黄金分割矩形可用直尺和圆规准确作出，其画法如图4-3（a）所示（AE≈EB），先作一个正方形ABCD，再以AB的中点E为圆心，EC为半径作圆弧与AB的延长线交于F；另一作图方法如图4-3（b）所示，先作正方形KLMN，以ML的中点O为圆心，OL为半径作圆弧交对角线OK于P，再以K为圆心、K P为半径作圆弧交K N于Q。

图4-3 黄金分割矩形作图法

3.黄金分割比例的特点

黄金分割比例能产生形象的重复性，使物体各部分产生丰富多彩的，既统一又多样的比例尺寸变化。它具有如下特点。

（1）按黄金分割比例划分的平面形状具有尺寸的多样性并兼有形状和方向的统一性，如图4-4所示的矩形，Ⅰ与Ⅳ在尺寸上有所对比，但有相同的形状和方向，它们亦重复了母长方形ABCD的形状与方向。

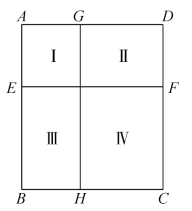
图4-4 黄金分割矩形的划分

（2）具有形状的多样性并兼有尺寸的统一性，如Ⅱ与Ⅲ在形状上不相同，但面积却相同。

（3）黄金分割比值具有重复性，线条与面积之比均为0.618，如图4-4所示。即

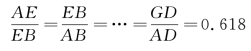(www.xing528.com)

如图4-5所示的ABCD是一个黄金分割矩形，过顶点B向对角线AC引垂线，交AD于E。再把矩形分成一个正方形S和另一个黄金分割矩形，再过EG与对角线AC的交点F作水平线，又可得到一个正方形S和又一个新的黄金分割矩形。如此反复推移，就可得到许多逐渐向心旋转的正方形S，这些正方形S的边长组成了黄金比例数列。黄金分割比例被广泛地应用于许多举世闻名的建筑物、绘画和其他艺术品中，汽车造型中也有采用，如图4-6所示。该图横坐标表示汽车总长，纵坐标表示汽车的轴距，斜线表示轴距与总长的各种比值。在汽车造型时，可从这些统计数据中找出汽车常用的比例，以供参考。

图4-6 汽车比例统计图

图4-5 旋转方形的矩形

应当指出，黄金分割比例并不是绝对的和唯一的，在物体造型时，通常根据需要还可采用简单的整数比、根号矩形以及其他级数关系等。

当处理三个以上的多参数比例而不是仅仅局限于长度、面积的两个参数间的比例时，就必须涉及数列的概念。有代表性的数列为

（1）等差数列：a，a+g，a+2gq，…，a+（n-1）g

（2）等比数列：1，a，a2，…，an-1

（3）斐波纳奇数列：1，3，5，8，13，P，Q，（P+Q）

（4）调和数列

（5）其他数列：贝尔数列，具有单摆运动构造的数列……

等差数列是变化固定的数列。等比数列是强有力的数列，其变化是基于几何数列的。斐波纳奇数列的变化在开始时无法造成圆滑的曲线，但是中途又接近等比数列，具有规则性的平稳；同时第n项的n之数目越大，那么它和前一项的比越接近黄金比。调和数列与等差数列相反，越后面的项，数字越小，随着项数的推进，不断接近某一定值。

4.比例划分举例

在造型的比例划分中，可对上述比例进行灵活运用。图4-7是典型的比例划分的一些例子。

图4-7 典型的比例划分举例

S—正方形 P形—1∶矩形，称为风景形 矩形—存在于等边三角形之中
φ矩形—1∶1.618矩形，或称海景形 矩形 θ矩形-1∶1+矩形
F—1∶1.236矩形，又称人物形 1.382—1∶1.382矩形

在造型设计中，采用一个或几个数列，或以一种或几种比例为基础，并使之巧妙地融合于物体的形体中，这将造成重复呼应、多样统一的良好效果。

应当指出，汽车造型中的比例和各部尺寸的确定并非出自造型设计，而是根据汽车的性能、结构、工艺等要求经过汽车总布置确定下来的。造型设计师的任务是在发现不合理的部分后协助或会同总布置设计师和结构设计师调整各部分的尺寸和比例，使各部的比例关系更加合理，达到统一协调、重复呼应的效果。