无水港的物流引力影响系数评价

综上所述，本书物流引力影响系数的提出是为了表示由于外界政策和其他外界因素的作用下一个节点对其他节点之间的物流引力能力的影响情况。基于现实和文献资料（Roso，2008；Samir et al.，2014），我们提炼出最应该关注的几个要素：地方政府或港口、口岸的物流成本补贴，通关流程便利性程度，节点间的铁路可达性等3个重要因素。这三个因素代表了当下中国在“一带一路”背景下内陆地区与沿海港口发展内陆腹地和无水港时所采取的主要措施，以及当前内陆地区与沿海港口或延边口岸之间物流通道基本情况，因此能够反映并代表各个节点对之间的外界环境和政策影响情况。

不同的外界因素在不同的节点对之间对于物流引力的影响情况不同。值得注意的是，相同外界因素在不同的节点对之间对物流引力的影响也可能不同。例如，宁波港为内陆腹地江西鹰潭和宁夏银川无水港到港的集装箱提供相同的物流成本补贴，但是由于宁波港与银川无水港之间的主要障碍是铁路运输通道的距离太长并且需要中转，影响了可达性，所以即使是相同的成本补贴但是对银川无水港的影响相对变弱了。相同影响因素在不同节点对之间的物流引力影响不同的特点恰好符合OWA 的特点。因此本书提出一个基于OWA算子的新方法，用于评价网络中每一节点对之间的物流引力影响系数值。

Yager（1988）在研究多指标决策问题时第一次提出了OWA 算子评价法。假设一个函数F：Rn→R，其中R 是一个实数集。U ＝（u1，u2，…，un）为一组给定的指标值向量，W ＝（w1，w2，…，wn）T是与函数F 相关的一组权向量。其中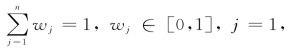2，…，n。 设vj是U 向量中第jth 大的元素。我们称函数F 为一个OWA 算子：

那么由OWA 算子获得的评价值矩阵A＝［aij］即为物流引力影响系数矩阵，计算过程如下：

假设由地方政府或港口企业提供的物流成本补贴为u1，通关手续简化程度u2，以及这些节点之间的铁路可达性u3，沿海港口和内陆口岸的总数为θ，共同构成向量X ＝（x1，x2，…，xθ）。

（a）由专家评价法获得无水港权重向量W ＝（w1，w2，…，wn）T。(www.xing528.com)

（b）确定评价矩阵。对于无水港i，i∀｛1，2，…，n｝，由相关物流专家对无水港i 与每一个海港和延边口岸节点x，x∀｛x1，x2，…，xθ｝构成的节点对，依照上述3个评价指标进行指标打分，获得评价矩阵Y ＝（yjk）θ×3，j＝1，2，…，θ，k＝1，2，3。

（c）对评价矩阵Y ＝（yjk）θ×3进行标准化处理，得标准化矩阵R ＝（rjk）θ×3，rj＝（rj1，rj2，rj3）。 按照OWA 算子理论，所有指标因素分为两类：一类是成本属性的，就是指指标值越大评价值越小；另一类是利益属性的，就是指标值越大评价值越大。本书的3个指标因素都属于利益属性的指标，其标准化方法如公式（4－12）所示（Goh et al.，1996）。

（d）集结评价。对于每一rj，j＝1，2，…，θ，用公式（4－13）得无水港i与任意x，x∀｛x1，x2，…xθ｝的物流引力影响系数。其中bk是rj的第k 大的元素。

（e）对每一无水港重复步骤（b）至（d），即可获得物流引力影响系数矩阵A ＝（aij）n×θ。