数值模型|机车免调式砂阀研制成果

砂阀的原理是通过高压高速空气使砂粒扬起、均匀喷出。砂阀基本结构原理如图3-1 所示。从图中可以看出，砂阀的上部为充气室，内部为高压气体。高压气体通过充气室下部的3个出口分别喷入砂阀内部，其中左侧两个喷嘴右侧一个喷嘴。砂阀的左侧接砂箱，通过3个喷嘴中间的喷嘴喷出高压气体将砂粒扬起压出，然后通过右侧的喷嘴将压出的砂粒加速喷至目标位置。左侧喷管上部挡板以及右侧喷管下部挡板的作用是在砂阀停止工作状态时防止砂粒泄漏。而最左侧的小喷嘴是通过喷气改变砂粒的运行轨迹，使砂粒具有向下的速度；同时最左侧的小喷嘴还能有效保护喷管，防止喷管被高速砂粒冲刷破坏。

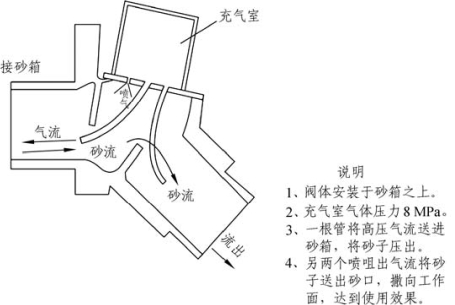
图3-1　砂阀基本结构原理图

根据砂阀的基本原理可知，在砂阀的设计过程中，评判砂阀的设计是否合理有3个关键因素：

（1）左侧吹砂压砂是否合理。

（2）喷管防冲刷是否合理。

（3）右侧喷管加速是否合理。

根据以上分析以及评判因素，结合fluent 软件建立了砂阀内气固两相流模型。模型中使用欧拉-拉格朗日方法分别对气相（空气）、颗粒相（砂粒）进行仿真，定量地计算得到砂阀中的气相场、颗粒轨迹线。气相控制方程如下方程中，ρ 为空气密度，p 为空气压力，g 为重力加速度矢量，u 和v 分别是空气和砂粒的速度矢量，T 为空气温度，τ 和τR 分别是剪应力和雷诺应力张量。

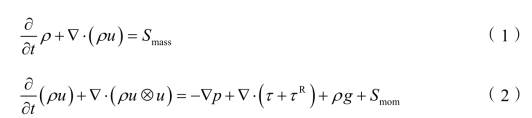
由于砂阀中空气流速速度较快，因此砂阀中流场流动为湍流流动，需要使用湍流模型来模拟该砂阀内的流动。RNG k-ε 湍流模型是Yakhot 及Orza 提出的一种改进的两方程k-ε 湍流模型。将非稳态N-S 方程对一个平衡态作Gauss 统计展开，并用脉动频谱的波数段作滤波的方法，从理论上推导出的高Re 数k-ε 湍流模型。RNGk-ε 湍流模型在形式上与标准的k-ε湍流模型完全相同，它的最大特点在于ε 方程的产生项系数 1C 的计算中引入了主流的时均应变率 Sij，这样 1C 不仅与流动情况有关，而且在统一问题中也还是空间坐标的函数。RNGk-ε 湍流模型如下

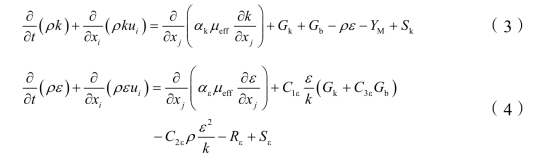
在这些方程中，Gk 表示由平均速度梯度而产生的湍流动能，Gb 是由浮力而产生的湍流动能，YM 表示在可压缩湍流中，波动扩张的全部耗散率，C1，C2，C3，是常量，ak 和ae 是k 方程和e 方程的湍流普朗特数的倒数，Sk 和Se 分别是用户定义的源项。

在RNG 理论中消除尺度的过程导出一个关于湍流黏度的微分方程

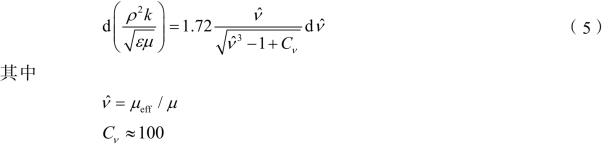
在高雷诺数限制下

从RNG 理论知，Cμ＝0.084 5。有趣的是这个值和标准k-e 模型的经验值0.09 很接近。

在流场分析的基础上，可以应用连续气流中离散相颗粒（砂粒）运动模型对砂粒运动轨迹进行预测计算。连续介质中离散的轨迹计算基于对颗粒力平衡方程的积分求解。空气中颗粒的力平衡方程为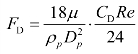；u 表示气流速度，up 表示颗粒速度，μ 为气体动力黏度，ρ 为气体密度，pρ 为颗粒密度，Dp 表示颗粒直径。雷诺数Re 的定义如下(www.xing528.com)

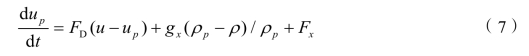
式中，FD 为单位质量颗粒所受到的气流阻力，

对于光滑的圆形颗粒，阻力系数CD 按下式计算

式中，常数a 由Morsi 或Alexander 的文献确定。公式右端第二项表示重力的影响。右端第三项为附加力，诸如颗粒加速的虚拟质量力和压力梯度引起的力、剪切升力等，在此不再赘述。为了考虑湍流气流脉动对颗粒散射的影响，采用随机行走模型确定气流的瞬时速度。

描述砂粒运动模型包含确定性轨道模型和随机轨道模型。确定性轨道模型中假设颗粒数总通量沿轨道保持不变，没有考虑颗粒湍流扩散，但实验表明在许多情况下颗粒湍流扩散是不可忽略的，直接用确定性轨道模型将会导致误差比较大。因此发展出了随机轨道模型，本模型中的砂粒计算将采用随机轨道模型。随机轨道模型是在瞬态颗粒动量方程的基础上，引入了浓度梯度与颗粒扩散系数的概念。

随机轨道模型的控制方程组

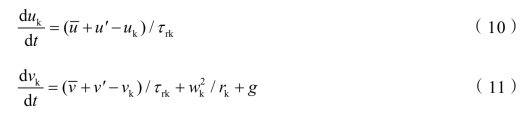
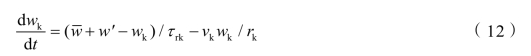
其中，uk，vk，kw 分别为颗粒的瞬时轴向速度、径向速度和切向速度，

及u′，v′，w′分别为气相在 3个方向上的时均速度和脉动速度，假设气相湍流是各向同性及局部均匀的，且随机速度分布满足Gaussian PDF 统计分布规律，得到气体速度的随机取样分布为

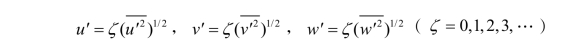
其中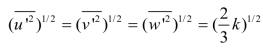，，且ζ 是随机数，将随机的u，v 和w 代入方程（10）、（11）、（12）来计算 uk，vk，kw 和，，颗粒与随机涡的相互作用时间可取为

随机轨道是用蒙特卡洛方法计算的，因为需要计算非常多的轨道，所以计算时间会比较长，但是计算精度较高。