轴测投影图的形成及施工图识读

轴测图是将形体连同直角坐标系，沿不平行于任一个坐标轴和坐标面的投射方向，用平行投影法将其投射到一个投影面上所得到的投影图。

如果根据平行投影的原理，如图1-34所示，将正方体和确定正方体空间的位置的三条坐标轴O′X′、O′Y′、O′Z′，沿不平行于这三条坐标轴和这三条坐标轴组成的坐标面的方向S，投射到新投影面P上，就得到三条轴测轴OX、OY、OZ和该形体的轴测投影。由于投射方向不平行于任一个坐标轴和坐标面，所以能在一个投影中同时反映出形体的长、宽、高和不平行于投射方向的平面，能够表示形体的形状，并可直接沿图上的长、宽、高三个方向度量对应的尺寸。

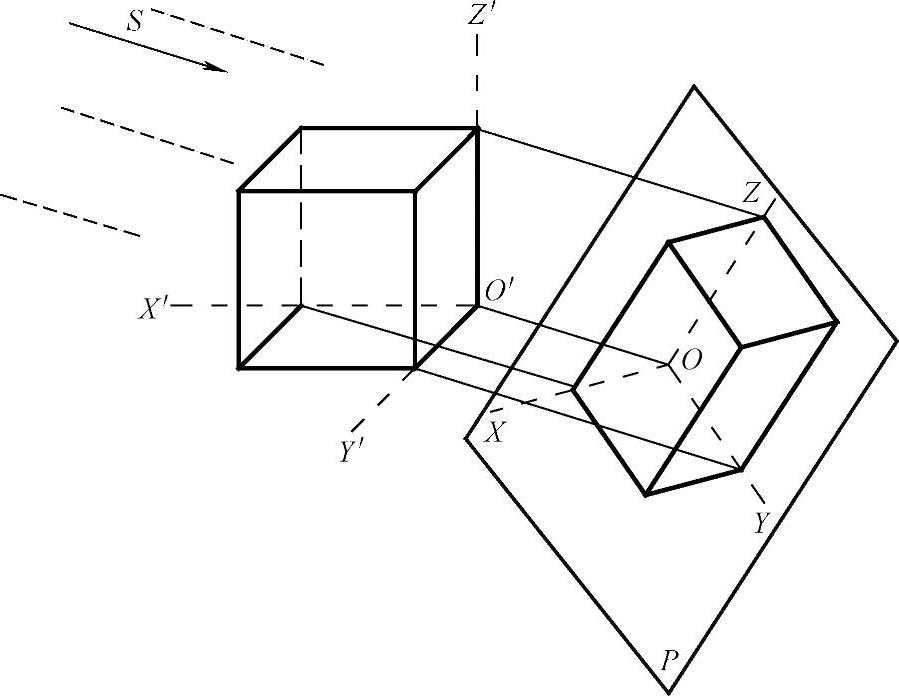
图1-34 形体轴测图的形成

轴测图有立体感是它的优点，但它也存在缺点。首先是对形体表达不全面，如图1-33中的形体，根据轴测图不能确定形体中间挖去的长方体的具体深度；其次，轴测图没有反映出形体各个侧面的实形，如形体上各矩形侧面在轴测图中变成了平行四边形，由于变形的关系，轴测图的作图会比较麻烦，尤其是外形或构造都比较复杂的形体。因此，在工程图样中，有些简单的形体可以用轴测图来代替正投影图；对于复杂的形体，轴测图作为辅助图样，表示形体的空间形状，用来表达形体和分析空间几何问题。

在轴测投影图中，如图1-35所示，投影面P称为轴测投影面；方向S称为轴测投射方向；三条坐标轴O′X′、O′Y′、O′Z′的轴测投影OX、OY、OZ称为轴测轴；轴测轴之间的夹角，即∠XOZ、∠XOY、∠YOZ称为轴间角；轴测轴上单位长度与相应的直角坐标轴上单位长度的比值称为轴向伸缩系数，如设直角坐标轴上取O′A′、O′B′、O′C′三段线段长，对应轴测轴上OA、OB、OC三段线段长，则有：(www.xing528.com)

1）OX轴向伸缩系数p=OA/O′A′。

2）OY轴向伸缩系数q=OB/O′B′。

3）OZ轴向伸缩系数r=OC/O′C′。

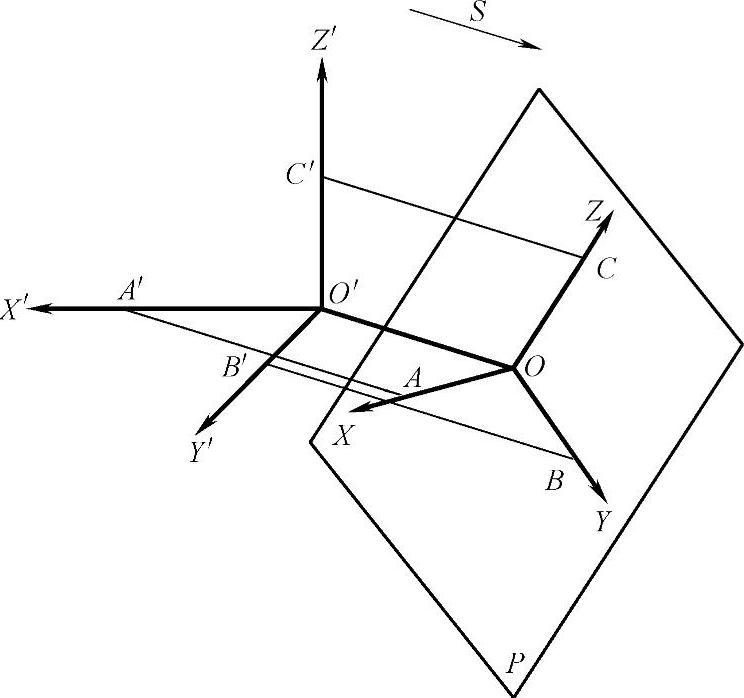
图1-35 轴测轴