点、直线、平面正投影施工图识读

一个形体（图1-4）是由多个侧面所围成的，各侧面又相交于多条侧棱，各侧棱又相交于多个顶点。所以，画形体的投影图，实质上就是画出形体的各个侧面及每条侧棱线的投影。因此，熟悉正投影条件下点、直线和平面的投影特性，是画出投影图的基础。

图1-4 空间形体

1.点的正投影

过空间点A向投影面H作垂直与该面的投射线，得到点A的正投影a，如图1-5a所示，故点的投影仍为点。点的一个投影不能确定它在空间的位置，如图1-5b中的点A₁、A₂、…、A_n的正投影都是点a。

2.直线的正投影

直线的投影为直线上任意两点投影的连线，因此，直线的正投影一般仍然是直线。若空间点在直线上，则它的投影必在该直线的投影上。

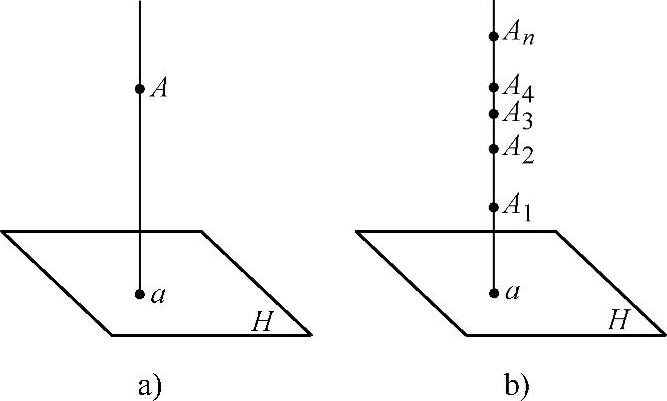
图1-5 点的正投影

对投影面来说，形体上的直线有各种不同的位置，有的垂直于投影面，称投影面垂直线（图1-6a）；有的平行于投影面，称投影面平行线（图1-6b）；有的相对于投影面是倾斜的，称一般位置线（图1-6c）。这三种直线投影特性各不相同，如下所述：

（1）投影面垂直线 投影是一个点，且该直线上任意一点的投影都在这个点上。投影面垂直线的这种特性称为直线投影的积聚性，如图1-6a所示，直线AB的投影积聚在a点上。

（2）投影面平行线 直线投射线的长度等于该直线的实际长度，如图1-6b所示，直线AB与其投影ab等长。

（3）一般位置线 直线投射线的长度小于该直线的实际长度，且直线上两线段长度的比值等于对应其投射线段长度的比，如图1-6c所示，直线投影ab的长度小于直线AB的长度，且l_as/l_sb=l_AS/l_SB。(www.xing528.com)

3.平面的正投影

平面可采用闭合线框围成的平面图形来表示。平面的正投影一般仍是平面。若平面上存在一条与投影方向相同的直线，则该平面的投影为一条直线。

平面对投影面的相对位置有三种情况，即平行、垂直和一般位置，其投影特性各不相同，如下所述：

（1）投影面平行面 投影的形状和大小与该平面实际的形状和大小相同，具有真实性。如图1-7a所示，平面ABC的形状和大小与投影abc的形状和大小相同。

（2）投影面垂直面 投影积聚成一直线，投影面垂直面的这种特性称为平面投影的积

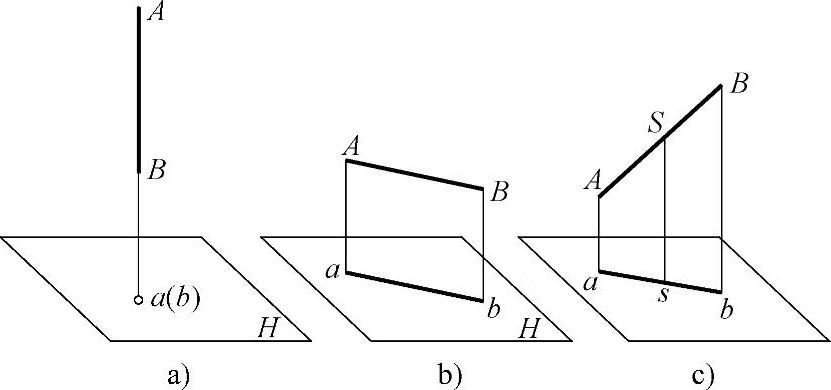
图1-6 直线的正投影

聚性。如图1-7b所示，平面上A点的投影a在直线bc上，平面ABC的投影就是直线bc。

（3）一般位置面 平面倾斜于投影面。投影是与原平面图形边数相同，投影对应，凹凸同性的图形，一般位置面的这种特性称为平面投影的类似性。但投影比平面图形本身的实形小。如图1-7c所示，平面ABC在投影面H上的投影abc小于平面ABC。

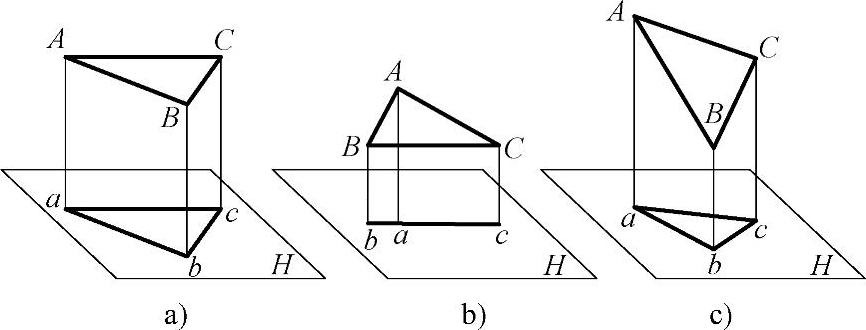
图1-7 平面的正投影