实用方法：基于地表沉降的乙烯管安全判定

7.3.1节建立了盾构穿越乙烯管的理论计算方法，该方法适用于在工程施工之前对穿越有可能造成的工程风险进行评估，以确定管线监测报警值使用。该方法以Peck公式为核心，根据材料性能以及材料力学、土力学的基本理论进行推导，建立的方法适用于盾构正交穿越乙烯管的过程分析。但是在实际工程中，盾构和乙烯管有时不是以正交穿越的形式存在，以虹梅南路隧道为例，盾构先后四次以平行、侧穿等方式穿越乙烯管，此种工况下，无法采用前文建立的理论方法进行分析，必须寻找新的方法来控制盾构穿越乙烯管过程的安全操作。

1.基本假设和过程推导

城市地下工程施工中，周围地下管线的安全性是施工中的重要问题，但多数情况下无法在管线上布置直接监测点来判定管线的安全性，而传统的地表位移监测控制方法往往只关心地表沉降的最大值，以此来控制管线的安全度。事实上，管线的应力状态和管线挠度是没有直接关系的，而是与挠度的二阶导数(曲率)存在定量关系。本节建立的方法就是通过一系列理论分析和假设条件，建立实测地表沉降和管线应力状态之间的关系，并通过与管线材料决定的容许应力的对比，判定其在盾构穿越条件下的安全度。根据图7.23建立基于实测地表沉降的乙烯管安全判定的具体方法如下。

根据盾构的埋深和地层条件计算盾构穿越影响范围W：

式中，W 为隧道推进影响范围；D 为隧道外径；Z 为隧道中心埋深；β为隧道影响角，一般取35°～50°，适用于软黏土、硬黏土及饱和粉细砂，一般强度越高，β取值越大。

根据隧道推进影响范围，沿管线长度方向布置若干地表沉降监测点，沉降监测点间距一般控制在W/4，有特殊需要时可适当加密。监测点布置如图7.24所示。

在盾构穿越管线过程中对监测点实施沉降监测，通常每12 h记录一次监测数据，以该区间上监测点的水平距离为x 坐标，监测点的沉降为y 坐标，可以得到n+1个坐标点。将监测数据以坐标形式{(x 1，y 1)，(x 2，y 2)，…，(x n+1，y n+1)}记录下来，以供后续分析使用。

将每次监测得到的坐标组{(x 1，y 1)，(x 2，y 2)，…，(x n+1，y n+1)}按照三次样条插值方法拟合为一组三次样条插值函数{S 1(x)，S 2(x)，…，Sn(x)}。拟合方法如下：

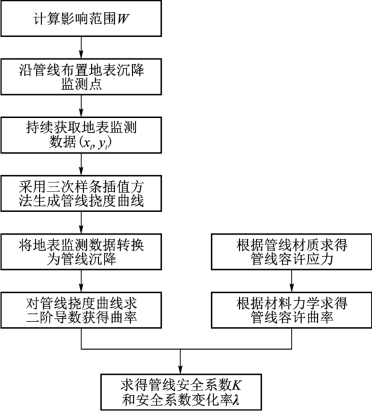
图7.23　管线安全度的判定方法

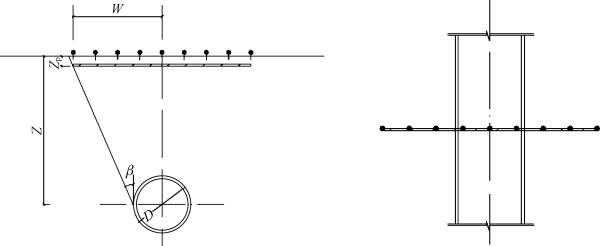
图7.24　测点布置剖面图

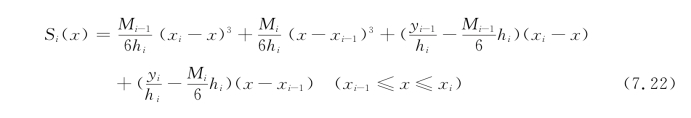
式中，M i为待定参数，可以根据以下方法求解。

对于自然状态下：

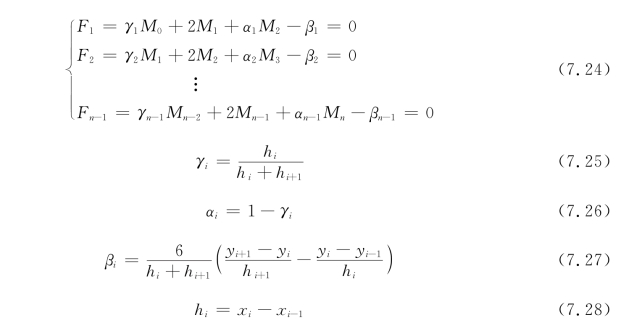
式中，i=1，2，…，n。

对于埋深0～3 m 的管线而言，考虑到地表监测点通常是埋设在地表以下1 m 左右的位置，其地表变形与管线变形可以认为是相同的。因此用三次样条插值方法拟合的曲线可以认为是管钱的挠曲线。

曲率求解：管线沉降曲线近似等于地表沉降曲线S(x)，假设管线符合梁理论，根据材料力学可以计算管线曲率

考虑到地埋管线的挠度远小于跨度，因此S′(x)远小于1，进而可以得到以下简化计算式：

计算管线的容许挠度：由材料力学梁弯曲理论有

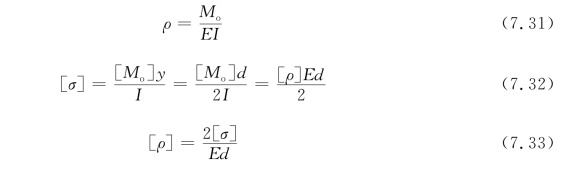
式中，ρ为梁曲率；M o 为梁弯矩；E 为管线材料弹性模量；I为管线材料沿中性轴的惯性矩；d 为管线直径；[σ]为管线材料容许应力；[ρ]为管线变形的容许曲率。

计算管线的安全度K：(www.xing528.com)

根据本节建立的算法，研究开发了一套变形曲线的挠度自动计算程序，可大大提高计算的效率及准确性。

2.盾构穿越乙烯管实测变形数据的安全度判定方法验证

为了验证前文建立方法的可用性以及超大直径盾构对地层扰动和乙烯管响应机制的适用性，本节以虹梅南路隧道西线970～1 030环穿越乙烯管监测数据为依据，给出乙烯管的安全判定结果。

图7.25所示为虹梅南路西线隧道第二次穿越乙烯管的监测点布置情况和盾构切口位置。穿越开始于1 018 环，至1 030环后盾尾脱出穿越出去，然后逐步远离。各监测点的实测沉降值如表7.10所列。

图7.25　乙烯管测点布置图和盾构切口位置

表7.10　盾构穿越乙烯管各测点的实测沉降值

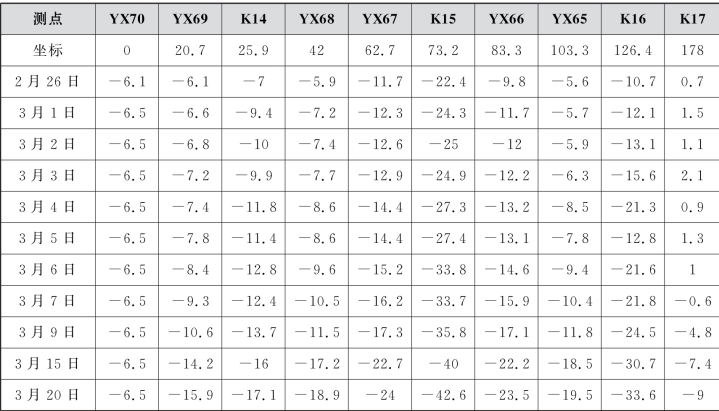
根据表7.10各测点的挠度可以绘制乙烯管在不同时刻的挠曲线，如图7.26和7.27所示，由此可以得到以下结论：

(1)盾构穿越过程中乙烯管的最大挠度为34 mm，位于测点K15。穿越后的后期沉降为43 mm。

(2)乙烯管挠曲线存在三个明显拐点，分别位于测点K15、K16以及YX65，其中K15的曲率最大，是整个穿越过程中乙烯管受力最大的位置。

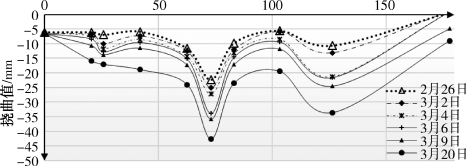
图7.26　乙烯管沿长度方向的挠曲线图

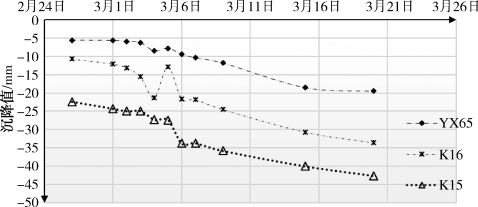
图7.27　挠度变化最大点的沉降历时曲线

将沉降监测数据输入到乙烯管安全判定程序中进行运算，可以得到每个测点不同时刻的曲率值(表7.11)。按照表7.8计算的乙烯管容许曲率3.91 mm-1可以计算出该盾构穿越过程中的乙烯管安全系数K，如表7.12和图7.28所示。需要说明的是，在安全系数计算中，两端点位置的曲率由于计算需要假设为0，因此安全系数值不包含测点YX70以及K17。

表7.11　盾构穿越乙烯管各测点的曲率值

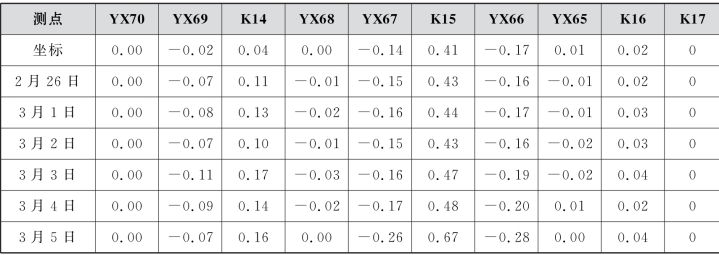
(续表)

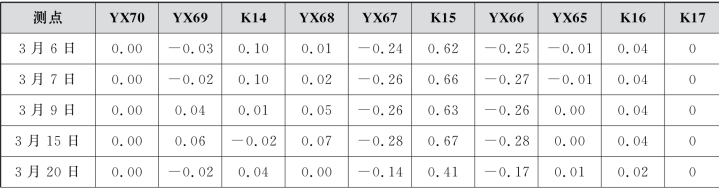
表7.12　盾构穿越乙烯管各测点的安全系数(K)

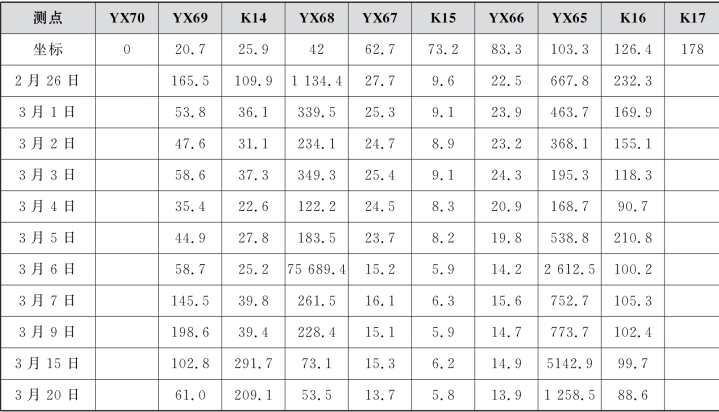
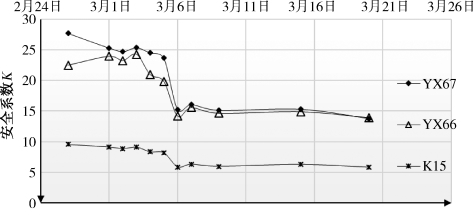
图7.28　盾构穿越乙烯管安全系数历时曲线

分析表7.12可知，在整个盾构穿越过程中，乙烯管的安全系数远大于1，说明乙烯管不会因为穿越造成的地层扰动导致的附加应力产生破坏。这也进一步证明了穿越过程中的盾构控制参数是合适的。通过对比分析可以发现，K15、YX67、YX66三个测点的安全系数较其他测点小，说明此处的扰动程度最剧烈。

图7.28表明，在盾构穿越之前，该乙烯管存在一定的先期变形，导致各个测点的安全系数并不一致，但是3月6日盾构穿越后，导致这三个测点位置的乙烯管安全度有明显下降。随后安全度的变化趋于平缓。盾构穿越导致的乙烯管局部变形对于管辖范围的影响最大。穿越完成后，尽管该位置的沉降会持续增大，但是乙烯管的安全度不会持续减小，这是因为后期沉降呈现出均一性的分布态势，各个测点共同沉降，管线的曲率不会产生明显的变化。