乙烯管破坏机制与安全度识别方法

7.3.1.1 现有管线安全度判定方法的局限性

研究盾构施工对上覆乙烯管线的影响，首先需要研究地埋乙烯管线的破坏机制，以及乙烯管在盾构推进模式下的变形特点。综合这两点才能建立具有理论依据的乙烯管安全判据。

目前我国国家和地方规范，并没有明确的根据管线的极限承载能力来判定管线安全度的方法。多数是根据设计和施工经验给出管线绝对变形量或者管节间相对变形(以角度控制)量来对施工过程进行控制。其中有代表性的方法如下：

(1)承插接口及机械铸铁管道或者柔性接缝管道最大变形为L/1 000。

(2)地表最大斜率为2.55 L/1 000(北京地铁、重庆地铁施工经验)。

(3)水平位移10～15 mm(上海市煤气管线保护标准)。

(4)水平位移0.6 mm/m；容许倾斜变形1～2 mm/m(德国建筑标准)。

上述安全判定标准的制定以多年建设经验为依据，采用施工过程中易于获取的监测数据为依据，经过简单计算即可对管线的安全性进行初步估计，便于工程使用。但是由于地下工程的复杂性，不同工程甚至同一工程的不同标段都有可能存在巨大的差异。采用同一标准进行判定的话，有可能过于保守甚至漏判安全隐患。因此有必要建立一种新的方法，从管线材料承载能力出发，建立一套安全、可信、易用的评价方法，解决超大直径盾构穿越过程中的管线安全问题。

7.3.1.2 以曲率控制的乙烯管破坏机制的理论计算方法

本节研究的主要目的是寻找盾构推进造成的地层扰动和上覆乙烯管附加变形之间的关系。通过乙烯管极限变形能力和盾构推进造成的管道附加变形之间的对比分析，对乙烯管的安全性进行预判。曲率控制方法的研究技术路线如图7.20所示。

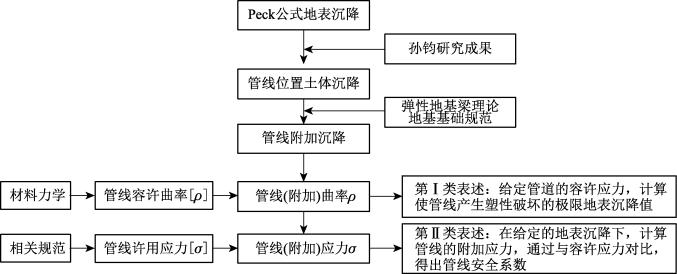
图7.20　曲率控制方法的研究技术路线

7.3.1.3 基本理论假设和过程推导

依照图7.20所示技术路线，计算模型简图如图7.21所示，假设隧道掘进方向与已有管线方向垂直，隧道中心埋深为Z，管线外径D，壁厚t，管线中心埋深为Z P。计算中做如下假定：

(1)管线材料为线弹性、均匀、各向同性；

(2)管线与地基土相互作用符合弹性地基梁假定；

(3)隧道开挖引起的地面沉降符合Peck公式。

1.容许曲率的计算

根据材料力学梁弯曲理论有：

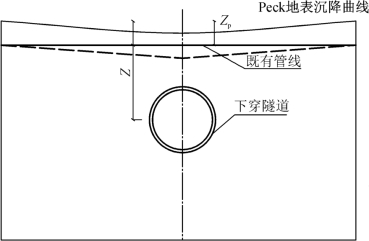
图7.21　受盾构穿越影响的管线变形示意图

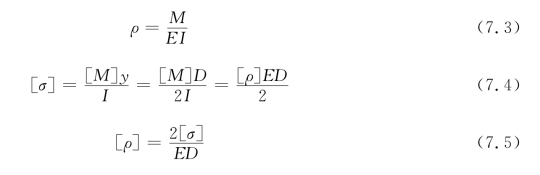
式中，ρ为梁曲率；M 为梁弯矩；E 为材料弹性模量；I为材料弹性模量；D 为梁高；[σ]为材料容许应力。

2.弹性地基梁变形系数

根据弹性地基梁理论：

式中，w 为地基梁挠度曲线；K 为地基基床系数；b为梁宽度；E p为管弹性模量；I p为管截面惯性矩。

3.根据Peck公式计算地表沉降

Peck在总结了大量盾构推进地表沉降的基础上，提出了Peck公式，其原理如图7.22所示。

隧道开挖引起的地面沉降计算如下：

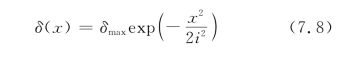
图7.22　Peck公式计算示意图

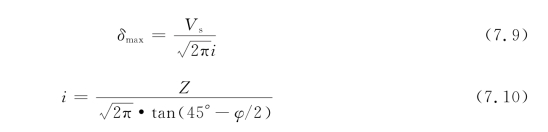
式中，δ(x)为沉降量；V s为地层损失率；i为沉降槽宽度系数；φ 为土体内摩擦角。

因此地表沉降槽宽度系数

(www.xing528.com)

根据施仲衡经验公式，管线处的沉降槽宽度系数i p 为

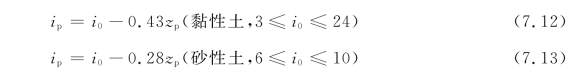
对于地表以下至隧道顶部平面以上的土层，地层损失的体积假设仍然成立，即地表面以下任意土层的沉降槽体积等于地层损失，沉降槽曲线仍是正态分布曲线。土层深度Z 增大，该土层距离隧道顶部的距离减小，土层的沉降槽宽度系数将会减小，δmax 和i两个系数将会随深度的不同而变化：

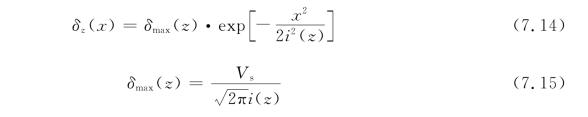
因此地表沉降控制值为

式中，ip 为管线处的沉降槽宽度系数；i 0 为地表的沉降槽宽度系数。

4.管线曲率和管线位置处土层最大沉降的关系

孙钧院士总结整理了当隧道掘进方向与管线方向垂直时管线最大曲率与管线处土层最大沉降量的关系：

式中，i p 为管线中心平面的沉降槽宽度系数；λ为弹性地基梁变形系数；δpmax 为管线位置处土层最大沉降量。

通过以上公式就可以建立管线的容许曲率和地表沉降最大值之间的关系，从而得到管线容许应力和地表沉降最大值之间的关系。

7.3.1.4 计算结果

根据前文建立的计算方法，以虹梅南路隧道盾构穿越乙烯管为例，计算乙烯管受盾构穿越影响的极限变形能力。计算参数如表7.7所列。

表7.7　计算参数取值表

根据上表计算乙烯管在盾构穿越条件下的极限变形能力有两种表述方式。第一类表述方式为给定管线的破坏极限(容许曲率)，然后根据前一节建立的方法反推地面的容许最大沉降。第二类表述方式是给定盾构穿越后的地面沉降最大值，然后求在此沉降数据下的乙烯管实际曲率，通过该曲率和容许曲率的对比，求得乙烯管的安全系数。这两种表述方式的计算结果分别如表7.8和表7.9所列。

1.第Ⅰ类表述方式：给定容许曲率求最大地表变形

由表7.8 可知，管线的容许曲率为3.91×10-3 m-1，此时地表容许的最大沉降为188 mm。应当说这对于超大直径盾构施工而言已经是一个非常大的沉降了，除非盾构出现事故，否则一般情况下不会出现如此之大的地面沉降数据。

表7.8　第Ⅰ类表述的计算结果汇总表

2.第Ⅱ类表述：给定地表沉降控制值，求解管道安全系数

若定义乙烯管安全系数为管道下部纤维实际应力和容许应力的比值，则可以求得该管道在给定地表沉降条件下的安全系数：

若以地表沉降控制值50 mm 为例，给出第Ⅱ类表述的管线安全系数计算结果。从表7.9 中可以看出，在盾构推进中心地表沉降50 mm 的情况下，乙烯管的安全系数仍然有3.77。

表7.9　第Ⅱ类表述的计算结果汇总表

7.3.1.5 理论计算结果的评述

根据上述理论计算方法和计算结果，针对虹梅南路隧道穿越乙烯管的施工，可以总结出以下基本注意事项：

(1)盾构下穿会对乙烯管造成一定程度的附加弯矩，特别是管道长时间埋入地下，劣化情况无法得知，在盾构施工过程中应特别引起注意。

(2)研究建立了乙烯管容许应力与盾构施工造成的最大地表沉降之间的关系。从现有的计算假设和各种资料基础上的计算可知，乙烯管具有较好的抗变形能力，在其达到塑性破坏时，极限地表沉降计算结果为188 mm，远大于一般意义上盾构施工造成的地表沉降。

(3)在采取措施将地表最大沉降控制在50 mm 以下时，乙烯管安全系数理论计算结果为3.77。若综合考虑管道劣化，取乙烯管容许应力折减系数为0.75时，管线的安全系数为2.82。

(4)施工过程中，应当建立严密的地表沉降观测和深层沉降监测机制。应当特别关注盾构推进断面的最大沉降，以及乙烯管断面的最大沉降。在斜穿乙烯管断面时，宜对监测点进行适当加密，并计算相邻三个测点之间的管道曲率半径，应当保证管道曲率半径不小于1 000 m(对应最大地表沉降为50 mm)。

(5)建议选取相似地层，对盾构穿越乙烯管进行模型试验，以验证管道受盾构下穿影响时的实际变形性态以及受力状态。收集试验相关参数和盾构推进控制参数，确保盾构穿越乙烯管过程中的安全。

(6)应严格控制盾构穿越期间及穿越后3～6个月的地面超载。