放热与散热分析结果及曲线-消防燃烧学

设有一个球形容器，体积为V，表面积为F，内部充满某种反应热为ΔH的可燃预混气体，现对其放热和散热进行分析。为使问题简化，作如下假设：

1）环境温度为T₀，反应开始时混气温度与环境温度相同，反应过程中混气的瞬间温度为T。

2）反应开始时容器的壁温与环境温度T₀相同，反应过程中，壁温升高，与混气温度相同。

3）反应过程中，容器内既无自然对流，也无强迫对流，容器内各点的温度、浓度相同。

4）着火前反应物浓度变化很小，近似认为不变。

5）环境与容器之间有对流换热，表面传热系数为α，它不随温度变化。

该分析模型的简化示意图如图4-2所示。

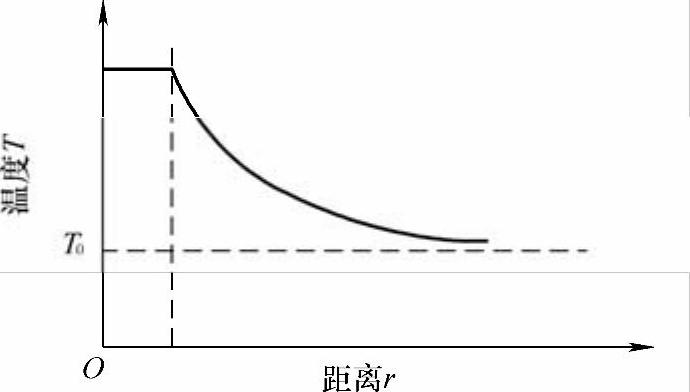
图4-2 热自燃理论分析模型的简化示意图

用Q_放表示混气在单位时间内由化学反应放出的热量，即放热速度，用Q_散表示混气在单位时间内向外界环境散发的热量，即散热速度，则(www.xing528.com)

Q_放=VΔHW_s （4-2）

Q_散=αF（T-T₀） （4-3）

式中 ΔH——可燃预混气体的化学反应热；

W_s——可燃预混气体的化学反应速度；

T——可燃预混气体温度。

根据燃烧反应速度方程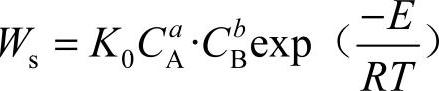可知，化学反应速度W_s与混气温度T成指数关系，所以Q_放是混气温度的指数函数，而Q_散则与混气温度成正比例关系。将Q_放和Q_散分别对混气温度T作图即得到放热曲线和散热曲线，如图4-3所示。不难理解，当混气浓度不同时，反应速度W_s不同，因而可得到一组放热曲线；当环境温度T₀不同时，可得到一组平行的散热曲线；当改变αF时，可得到一组斜率不同的散热曲线。

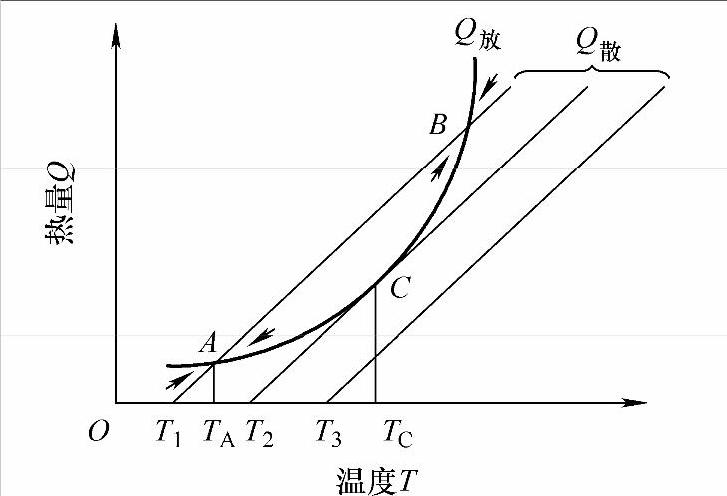
图4-3 放热曲线与散热曲线