简支梁的绝对最大弯矩在建筑力学（第2版）中提供

由前面的讲述我们知道,简支梁的弯矩包络图反映了所有截面弯矩的最大值,其中的最大竖标值是所有截面最大弯矩中的最大值,称为绝对最大弯矩,用Mmax表示。绝对最大弯矩无疑是考虑移动荷载作用时结构分析、设计的重要依据。可以通过作出弯矩包络图来得到绝对最大弯矩,但这种方法计算量大,而且精度也不高,因此一般不采用此方法来计算绝对最大弯矩。下面介绍一种较为简便的方法。

由于简支梁在移动荷载作用下,其上任一截面都有最大弯矩,其值可以通过确定该截面弯矩的最不利荷载位置,并计算该荷载位置时的弯矩而得到。那么,要得到简支梁的绝对最大弯矩,就必须知道:(a)绝对最大弯矩发生在哪一个截面?(b)此截面发生最大弯矩时的荷载位置。

当梁在集中荷载组作用下,无论荷载处于什么位置,弯矩图的顶点总是在集中荷载作用的截面处,也即在任何荷载位置时,梁的最大弯矩一定发生在某个集中荷载作用的截面上。因而,可以断定:绝对最大弯矩必定发生在某一集中荷载作用处的截面上。剩下的问题便是确定绝对最大弯矩究竟发生在哪一荷载位置的哪一个集中荷载作用处。为此,可先任选一集中荷载,看荷载处于什么位置时,该荷载作用处的截面弯矩达到最大值。按相同的方法,依次计算出各荷载作用点处截面的最大弯矩,加以比较,即可确定出绝对最大弯矩。

如图17.21(a)所示的简支梁,受一组移动集中荷载作用。取梁上的某一集中荷载FK,设FK到左支座A的距离为x。

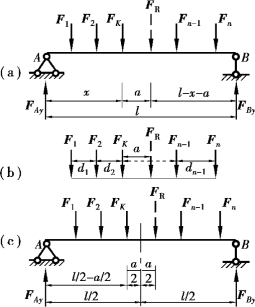
图17.21

梁上所有荷载的合力为FR=F1+F2+FK+…+Fn-1+Fn=到FK的距离为a。以FK的作用点为矩心,根据合力矩定理可得

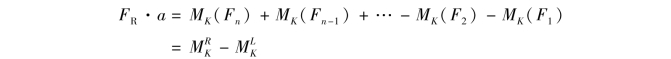
于是有

式中,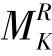,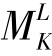分别为FK以右梁上和以左梁上的荷载对FK作用点的力矩总和。由于集中荷载组中各荷载之间的距离是固定的,如图17.21(b)所示,d1,d2,…,dn-1,dn均为常数,并不会随整个荷载组的移动而变化。显然,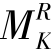,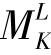也是与x无关的常数,因此,合力FR到FK的距离a也是常数。当合力FR位于FK的右侧时,a为正;而当FR位于FK的左侧时,则a为负。

以全梁为研究对象,可求得左支座A的反力为

FK作用点处截面上的弯矩Mx为

当Mx为极大值时,根据极值条件

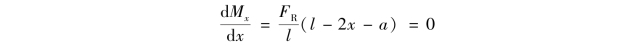
由此可得,最大弯矩的截面位置为

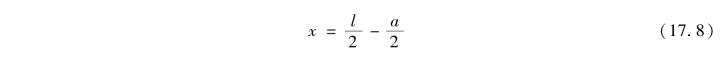
该式表明,当FK与合力FR对称于梁的中点放置时,如图17.21(c)所示,FK作用点处截面上的弯矩达到最大值,其值为

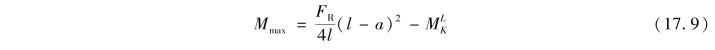
采用上述方法,可以计算出每个荷载作用点截面的最大弯矩,然后进行比较就能得到绝对最大弯矩。但是,当梁上的集中荷载较多时,采取这种方式会比较麻烦。实际计算时,应先预估发生绝对最大弯矩的临界荷载。经验表明,使梁中点截面发生最大弯矩的临界荷载就是发生绝对最大弯矩的临界荷载。因此,计算简支梁绝对最大弯矩的步骤为:

①确定使梁中点截面C发生最大弯矩的临界荷载FK,并求出梁中点截面C的最大弯矩MCmax。

②根据梁上布置的荷载个数求出其合力FR的大小和相对于FK的位置。(www.xing528.com)

③移动荷载组使FK与合力FR对称于梁的中点放置,此时必须注意检查移动后梁上的荷载是否与前面计算合力时相符,如有变化(即有荷载被移到梁之外或有新的荷载移至梁上),则应重新计算合力,并再次将FK与重新计算的合力FR对称于梁的中点放置,直至荷载移动前后梁上的荷载没有变化。

④按式(17.9)计算FK作用点处截面上的弯矩,通常就是绝对最大弯矩Mmax。

还应注意,如果假设梁上放置不同的荷载个数均能实现上述荷载布置时,则应将不同情况下FK作用点处截面上的弯矩分别求出,然后取最大者为绝对最大弯矩。

【例17.4】　试求如图17.22(a)所示简支梁在两台吊车荷载作用下的绝对最大弯矩,并与跨中截面最大弯矩进行比较。已知F1=F2=F3=F4=152kN。

【解】　①求跨中截面C的最大弯矩。绘出MC影响线,如图17.22(b)所示,显然F2(或F3)位于C点时是MC的最不利荷载位置〔图17.22(a)〕,MC的最大值为

MCmax=152×(0.6+3.0+2.28)=893.76(kN·m)

②求绝对最大弯矩。

a.考虑4个荷载全作用在梁上的情况,令F2=FK,此时

将F2与FR对称于梁的中点,荷载位置如图17.22(c)所示,此时4个荷载全在梁上,与求合力时相同,由式(17.9)可计算得此荷载位置时F2作用点截面的最大弯矩为

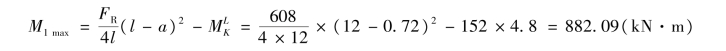
b.考虑3个荷载作用在梁上的情况,令F3=FK,此时

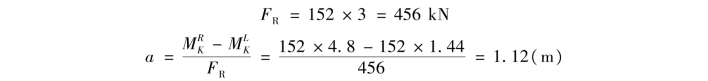
将F3与FR对称于梁的中点,荷载位置如图17.22(d)所示,此时最左边的荷载F1被移到梁之外了,只有3个荷载在梁上,与求合力时相同,由式(17.9)可计算得此荷载位置时F3作用点截面的最大弯矩为

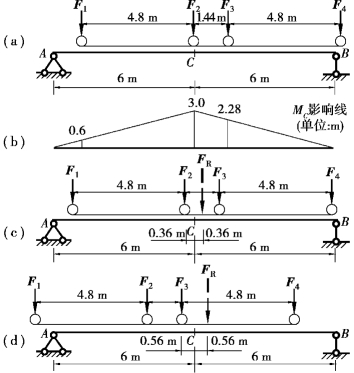
图17.22

经过比较可知,在如图17.22(d)所示的荷载位置时F3作用点的截面发生绝对最大弯矩,其值为

Mmax=M2max=905.68kN·m

③比较绝对最大弯矩与跨中截面的最大弯矩。

即绝对最大弯矩比跨中截面最大弯矩大1.3%。在工程实际中,有时也用跨中截面最大弯矩来近似代替绝对最大弯矩。