建筑力学（第2版）：确定最不利荷载位置

承受移动荷载作用的结构,其上的量值通常都会随着荷载的移动而变化。将使某量值产生最大(或最小)值时的荷载位置称为该量值的最不利荷载位置。对受移动荷载作用的结构进行设计前,必须先要确定某一量值的最不利荷载位置,并计算出该荷载位置时量值的大小即最大(或最小)值,然后在此基础上才能进行设计。下面按荷载的类型分别讨论如何利用影响线来确定最不利荷载位置。

(1)移动均布荷载作用时的最不利荷载位置

如果移动荷载是长度不定、可以任意分布的移动均布荷载时,根据式(17.2)可知,最不利荷载位置是在影响线〔图17.11(a)〕的正值部分布满荷载(求最大正值),如图17.11(b)所示;或在影响线负值部分布满荷载(求最大负即值最小值),如图17.11(c)所示。

【例17.2】　试计算如图17.11(a)所示外伸梁在长度可任意布置的移动均布荷载作用下,截面C的最大弯矩MCmax和最小弯矩MCmin。已知荷载集度大小为q=25kN/m。

【解】　①画出MC影响线,如图17.11(b)所示。

②当均布荷载布满影响线的正值部分即AB段时,便是MC取最大值的最不利荷载位置,如图17.11(c)所示。因此有

③当均布荷载布满影响线的负值部分即DB和BE段时,便是MC取最小值的最不利荷载位置,如图17.11(d)所示,因此有

图17.11

如果移动荷载是长度固定的均布荷载,如图17.12(a)所示。在影响线为三角形的情况下,根据式(17.2),最不利荷载位置是使均布荷载对应的面积A为最大。可以证明,当均布荷载作用范围起点和终点对应的影响线竖标相等时,均布荷载作用范围所对应的面积为最大,如图17.12(b)所示,当yC=yD时,A为最大。因此,最不利荷载位置是使均布荷载两端点对应的影响线竖标相等的位置。

图17.12

(2)移动集中荷载作用时的最不利荷载位置

对于移动集中荷载,由可知,当最大时所对应的荷载位置即为S的最不利荷载位置。下面分几种情形进行讨论。

①若只有一个移动集中荷载作用在结构上,显然当该荷载位于影响线的最大竖标处即为最不利荷载位置。

②若有两个移动集中荷载F1,F2同时作用在结构上,两个荷载中数值较大的位于影响线最大竖标处,而且把另一个荷载放在影响线坡度较缓的一侧即为最不利荷载位置,如图17.13所示。

图17.13

③如果有一组(三个及三个以上)移动集中荷载同时作用在结构上,最不利荷载位置将难于凭直观确定。但根据最不利荷载位置的定义可知,当荷载在最不利荷载位置时,所求量值S为最大,因而荷载组由该位置不论向左还是向右稍许移动,都将使得量值S减小。为此,可以通过分析荷载移动时S的增量来确定此类情况下的最不利荷载位置。

我们以常用的影响线为三角形的情况来分析。如图17.14(c)所示为某量值S的影响线,该影响线左直线的倾角为α,右直线的倾角为β。设坐标轴x向右为正,y向上为正;倾角以逆时针方向为正,顺时针方向为负,故α为正,而β则为负。

图17.14

现有一组间距不变的集中荷载组处在如图17.14(a)所示的位置,用FR1表示与影响线左直线对应范围内各荷载的合力,用FR2表示与影响线右直线对应范围内各荷载的合力。由式(17.2)可得在图17.14(a)所示的荷载位置时所产生的量值为

S=FR1y1+FR2y2

当整个荷载组向右移动一微小的距离Δx时,如图17.14(b)所示,此时的量值为

则量值的增量为

由图17.14(c)可知

于是有

由前面的分析我们已经知道,要使S成为极大值的条件是:荷载自该位置无论向左或向右移动微小距离,S都将减小,即ΔS<0。由于荷载向左移时Δx<0,而右移时Δx>0,同时在如图17.14(c)所示的S影响线中的h>0,因此使S成为极大值应满足的条件是

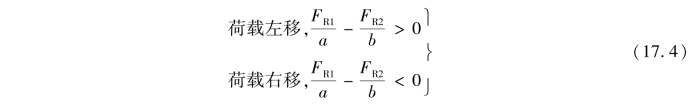
上式表明,荷载向左、向右移动微小距离时,必须变号,S才可能成为极大值。(www.xing528.com)

在什么情况下才可能变号呢?式(17.4)中a,b是与量值S影响线左右直线相对应的长度,是常数,它们并不会随荷载的位置而改变。因此要使荷载向左、向右移动微小距离时变号,就必然要左右两直线对应范围内荷载的合力FR1,FR2的大小发生改变,显然这只有当某个集中荷载正好作用于影响线的顶点处时才有可能。当然,不是每个集中荷载位于影响线的顶点时都能使变号。我们将能使变号的集中荷载称为临界荷载,用FK表示,此时的荷载位置称为临界位置。

由以上分析可知,确定临界荷载的具体方法是:从荷载组中取一集中荷载,令其为FK,并将该荷载放置到影响线的顶点对应的位置处。同时,计算出Fk左右两侧荷载的合力,如图17.15所示。

图17.15

当荷载组向左移时,;

当荷载组向右移时,。

由式(17.4)可得,如果FK能满足

则FK即为临界荷载,相应的荷载组所处的位置即为临界位置。因此,将式(17.5)称为影响线为三角形的临界位置判别式。显然,临界荷载的特点是:将临界荷载移到影响线的哪一侧,哪一侧的平均荷载就大一些。

一般情况下,临界位置可能不止一个。可以用以上方法找出所有的临界位置,并计算出每个临界位置所对应的量值,经比较绝对值最大者即为该量值的最大值,它所对应的荷载位置即为最不利荷载位置。

应当注意,在荷载向右或向左移动时,可能会有某一荷载被移到梁之外了,在利用临界荷载判别式(17.5)时,∑F左和∑F右中应不包含已离开了梁的荷载。

当然,对于固定长度的移动均布荷载跨过三角形影响线顶点时的临界位置,我们也可以用类似的方法来确定。如图17.16所示,S成为极值应满足条件。由前面的分析可得

图17.16

于是有

即左、右两侧的平均荷载应相等。

【例17.3】　如图17.17(a)所示,简支梁受两汽车荷载作用,试求截面K的最大弯矩MKmax。

图17.17

【解】　①绘制MK影响线,如图17.17(b)所示。

②确定临界荷载。根据梁上荷载的排列,判断可能的临界荷载是130kN。令FK=130 kN,则。由判别式有

(注意:将FK=130kN置于截面K处,当荷载组向右移动微小距离时,最右边的100kN荷载刚好被移除梁之外,此时∑F右=50kN)

FK=130kN满足判别式,因此是临界荷载。

③确定最不利荷载位置。经分析,虽然100kN也是临界荷载,但很明显,临界荷载为100kN时截面K的弯矩小于临界荷为130kN时的弯矩。因此,当130kN作用在截面K处时的荷载位置是MK的最不利荷载位置。

④计算最大弯矩MKmax。根据影响线中与最不利荷载位置中各荷载对应的竖标可得

我们必须注意,如果量值的影响线是直角三角形(包括影响线的竖标有突变的情况),判别式(17.5)、式(17.6)将不再适用。此时的最不利荷载位置,如果荷载比较简单,可直观判定。如图17.18所示的影响线,行列荷载中各集中荷载的大小相等,即F1=F2=F3=F4,显然当F1位于影响线的顶点时所产生的S值最大,故为最不利荷载位置。

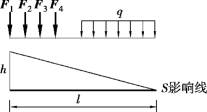
图17.18

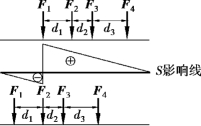
图17.19

当荷载比较复杂时,可按前面估计最不利荷载位置的原则,布置几种荷载位置,并计算出每种荷载位置时的S值,其中产生最大S值的荷载位置即为最不利荷载位置。例如图17.19所示影响线,如果荷载间的关系为F1=F2>F3=F4,则只需分别将F1,F2放置在影响线突变点的正竖标(即突变点右侧)处,并求出两种荷载位置时的S值,其中最大S值对应的荷载位置便是使量值S为最大值的最不利荷载位置。