简支梁和外伸梁的影响线绘制方法

(1)反力影响线

如图17.5(a)所示的外伸梁,取A点为坐标原点,横坐标x以向右为正。当荷载F=1作用于梁上任一点x时,由静力平衡条件可分别求得反力FAy,FBy的影响线方程为

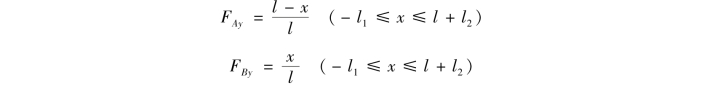
以上两个方程与相应的简支梁的反力影响线方程完全相同,只是x的取值范围有所扩大,因此,只需将相应简支梁的反力影响线向两个外伸部分延长,即可绘出整个外伸梁的反力FAy和FBy的影响线,分别如图17.5(b)、(c)所示。

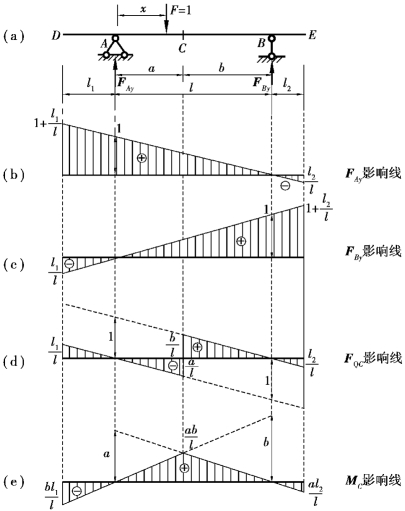
图17.5

(2)跨内部分截面内力影响线

如图17.5(a)所示,截面C为两支座之间的截面。当F=1在截面C以左移动时,取截面C以右部分为隔离体,由静力平衡条件可求得影响线方程为

FQC=-FBy　(-l1≤x<a)

MC=FByb　(-l1≤x≤a)

当F=1在截面C以右移动时,取截面C以左部分为隔离体,由静力平衡条件可求得影响线方程为

FQC=FAy　(a<x≤l+l2)

MC=FAya　(a≤x≤l+l2)

由上可知,FQC和MC的影响线方程也与简支梁的相同。因而与绘制反力影响线一样,只需将相应简支梁的FQC和MC的影响线向两外伸臂部分延长,即可得到外伸梁的FQC和MC的影响线,分别如图17.5(d)、(e)所示。(www.xing528.com)

(3)外伸端部分截面内力影响线

绘制外伸端部分任一指定截面K〔图17.6(a)〕的剪力和弯矩影响时,为计算方便,取K点为坐标原点,并规定x轴向左为正。当F=1在截面K以左移动时,取截面K以左部分为隔离体,由静力平衡条件可列出剪力FQK和弯矩MK的影响线方程为

FQK=-1　(0<x≤c,DK段)

MK=-x　(0≤x≤c,DK段)

当F=1在截面K以右移动时,仍取截面K以左部分为隔离体,由静力平衡条件显然可得出

FQK=0　(c-l1-l-l2≤x<0,KE段)

MK=0　(c-l1-l-l2≤x≤0,KE段)

实际上,由当荷载只作用在基本部上附属部分不受力的特点,很容易得出当F=1在梁的KE段移动时,FQK=0和MK=0这一结论。由上述得到的影响线方程可绘出FQK和MK的影响线,如图17.6(b)、(c)所示。

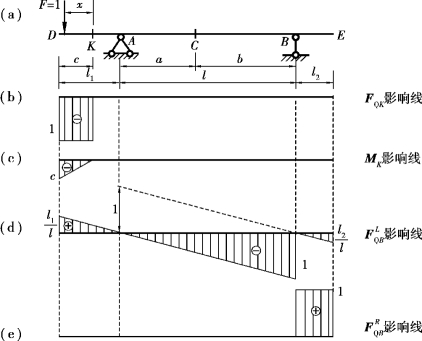
图17.6

若要绘制外伸梁支座处截面的剪力影响线,则要针对支座左侧的截面和支座右侧的截面分别讨论。这是因为,外伸梁支座左右两侧的截面分别属于跨内部分和外伸端部分。例如支座B左侧截面属于跨内部分截面,因此其剪力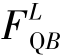的影响线可由FQC的影响线〔图17.5(d)〕使截面C趋近于截面B左侧而得到,如图17.6(d)所示;而支座B右侧截面则属于外伸端部分截面,其剪力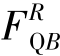的影响线则可由外伸端BE部分趋近于支座B右侧的截面剪力影响线得到,显然很容易画出,如图17.6(e)所示。

以上分别介绍了简支梁和外伸梁两种单跨静定梁影响线的绘制。另一种单跨静定梁——悬臂梁截面内力的影响线绘制方法与外伸梁外伸端部分截面内力影响线的绘制方法完全相同。

通过以上的讨论可以发现,静定结构的反力和内力影响线方程都是x的一次函数,因此静定结构的反力和内力影响线都是由直线段所组成。而超静定结构的反力和内力影响线则一般为曲线。