简支梁影响线-建筑力学第2版

(1)反力影响线

设要绘制如图17.3(a)所示简支梁反力FAy的影响线。取支座A为原点,梁轴线AB为x轴,向右为正,以坐标x表示单位集中荷载F=1的作用位置。当F=1移动到梁上的任意位置(0≤x≤l)时,取全梁为研究对象,画其受力图,并设反力向上为正,由静力平衡条件

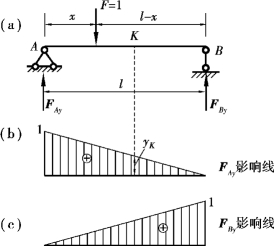
图17.3

则有

得

此式即为反力FAy的影响线方程。由此可见,FAy将随x的变化而变化,并且是x的一次函数,因此FAy的影响线是一条直线段,只需要确定两点即可画出该直线段:

当x=0时,FAy=1

当x=l时,FAy=0

将这两点用直线相连,即可绘制出FAy的影响线,如图17.3(b)所示。绘制影响线时,常规定正的竖标画在基线的上侧,负的竖标画在基线的下侧,并要标注正负号。

在此必须强调,FAy的影响线图中所有的竖标代表的是当F=1作用在相应位置处时,反力FAy的大小。例如图17.3(b)中的yK代表的是当F=1作用在K位置处时反力FAy的大小。

同理,对于反力FBy ,由静力平衡条件,则有

FByl-Fx=0

即可列出FBy的影响线方程

显然也是x的一次函数,因此FBy的影响线同样是一直线段,只需要确定两点:

当x=0时,FBy=0

当x=l时,FBy=1

即可绘制出FBy的影响线,如图17.3(c)所示。

由于F=1的量纲为1,所以反力影响线竖标的量纲也为1。今后在利用影响线研究实际荷载的影响时,应乘以实际荷载的相应单位。

(2)剪力影响线(www.xing528.com)

现绘制如图17.4(a)所示简支梁截面C的剪力FQC影响线。仍取A点为坐标原点,x表示单位集中荷载F=1的作用位置。当F=1作用于截面C以左或以右时,剪力FQC具有不同的表达式,应分段考虑。

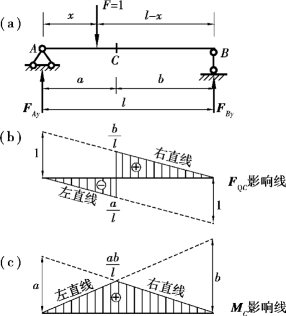
图17.4

当荷载F=1在截面C以左的梁段AC上移动时,为计算方便,取截面C右边部分为隔离体,并以绕隔离体顺时针转向的剪力为正,由静力平衡条件,可得FQC的影响线方程为

由此可知,FQC影响线在截面C以左部分为一直线。

当x=0时,FQC=0

当x→a时,

于是可绘出当荷载F=1在截面C以左的梁段AC上移动时FQC影响线,如图17.4(b)所示。

当荷载F=1在截面C以右的梁段CB上移动时,上面列出的FQC影响线方程显然不再适用。此时,可取C左边部分为隔离体,由静力平衡条件,可得FQC的影响线方程为

可见,FQC影响线在截面C以右部分也是一直线。

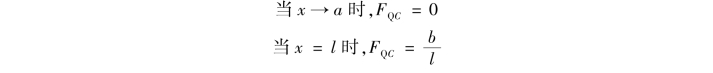
于是可绘出当荷载F=1在截面C以右的梁段CB上移动时FQC影响线,如图17.4(b)所示。剪力影响线的竖标是量纲为1的量。

由以上分析可知,FQC影响线由两段互相平行的直线所组成,通常将截面C以左的直线称为左直线,截面C以右的直线称为右直线。由上述剪力FQC影响线方程可知,将反力FBy影响线反号并取其AC段即可得FQC影响线的左直线,而直接利用反力FAy影响线并取其CB段即可得FQC影响线的右直线。FQC影响线的竖标在C点处有一突变,也就是当F=1从C点左侧移到其右侧时,截面C上的剪力值将发生突变,突变的大小等于1。而当F=1正好作用在C点时,FQC的值是无法确定的。

(3)弯矩影响线

现绘制如图17.4(a)所示简支梁截面C的弯矩MC影响线。当荷载F=1在截面C以左的梁段AC上移动时,为计算方便,取截面C右边部分为隔离体,并以使梁下侧纤维受拉的弯矩为正,由静力平衡条件,可得MC的影响线方程为

上式表明,将反力FBy影响线乘以b并取其AC段即可得MC影响线的左直线,如图17.4(c)所示。

同理,当荷载F=1在截面C以右的梁段CB上移动时,可取C左边部分为隔离体,由静力平衡条件,可得MC的影响线方程为

上式表明,将反力FAy影响线乘以a并取其CB段即可得MC影响线的右直线,如图17.4(c)所示。显然,弯矩影响线的竖标是量纲为长度的量。

由以上分析可知,MC影响线由两段相互的直线所组成,形成一个三角形,两直线的互点即为三角形的顶点正好位于截面C处,其竖标。当F=1恰好作用于C点时,弯矩MC达到最大值。