建筑力学第2版：影响线的概念

前面各章在计算结构的各种量值(包括支座反力、截面内力和位移等)时,作用在结构上的荷载大小、方向及作用位置都是固定不变的,这类荷载称为固定荷载。结构在固定荷载作用下,其支座反力和内力都是固定不变的。但在工程实际中,有些结构除了要承受固定荷载作用外,还要承受移动荷载的作用。例如,桥梁承受在其上行驶的汽车、火车和活动的人群的荷载,厂房的吊车梁承受在其上运行的吊车的荷载等,这些荷载的作用位置在不断变化,均为移动荷载。显然,结构在移动荷载作用下,其支座反力和内力都将随荷载位置的变动而变化。因此,在结构设计时,必须要求出在移动荷载作用下反力和内力的最大值,为此,就要研究荷载移动时反力和内力的变化规律。然而,在移动荷载作用下,不同量值的变化规律是不相同的。例如图17.1所示的简支梁,当汽车在梁上从左向右行驶时,支座A的反力逐渐减小,而支座B的反力却在逐渐增大;同样,在汽车的行驶过程中,同一截面上的弯矩与剪力的变化规律也是不相同的。因此,研究移动荷载对量值的影响时,一次只能讨论一个反力或某截面上的某个内力的变化规律。

工程实际中的移动荷载通常是由许多间距不变的竖向荷载所组成(如火车、汽车的荷载是通过轮距不变的车轮传递到梁上的),而且类型很多,不可能逐一加以研究。为简便起见,我们可先来研究一种最简单情况,即一个竖向单位集中荷载F=1在结构上移动时,对结构的某一指定量值(例如某一反力或某一截面上的某一内力等)所产生的影响,再根据叠加原理就可进一步研究结构在各种移动荷载作用下对该量值的影响。

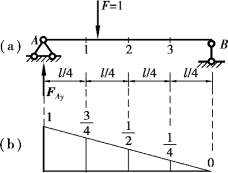
如图17.2所示的简支梁,当竖向单位集中荷载F=1分别移动至A,1,2,3,B各等分点时,由静力平衡条件可求得支座A处的反力FAy分别为。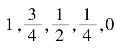

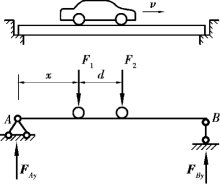
图17.1

(www.xing528.com)

图17.2

现以横坐标表示单位荷载F=1的作用位置,以纵坐标表示FAy的大小,并将各对应点处FAy的大小在水平基线上用竖标绘出,再用曲线将各竖标的顶点连起来,这样就得到了如图17.2(b)所示的图形,该图形反映了竖向单位集中荷载F=1沿梁移动时支座反力FAy的变化规律,将这一图形称为支座反力FAy的影响线。即:当一个定向单位集中荷载(常常为竖直向下的)沿结构移动时,反映某一指定量值(某个支座反力或某截面的弯矩或剪力)变化规律的图形,称为该量值的影响线。

绘出某量值的影响线后,就可利用叠加原理确定出结构在具体的移动荷载作用下,该量值产生最大值的荷载位置(即最不利荷载位置),进而求出该量值的最大值,为结构设计提供依据。

下面先介绍影响线的绘制,然后讨论影响线的应用。