计算多结点连续梁和无侧移刚架的力矩分配法（建筑力学第2版）

用力矩分配法计算只有一个刚结点的连续梁和无侧移的刚架时,只需进行一次分配、一次传递,再进行叠加即可求出各杆端弯矩,并且得到的是精确解答。用力矩分配法计算具有多个刚结点的连续梁和无侧移的刚架时,由于各个结点之间有相互传递弯矩的影响,一次分配计算就不能保证所有结点的平衡,而需要多次重复计算,将相互间的传递弯矩再进行分配计算。经过几轮循环重复计算,传递弯矩会越来越小,最后趋近于零,此时结点就接近于平衡。最后把各杆端每次分配计算得到的分配弯矩、传递弯矩及原先的固端弯矩叠加,即可得到各杆端的最终弯矩。

下面以如图16.5(a)所示的三跨连续梁为例,来说明力矩分配法计算多结点连续梁和无侧移刚架的过程。连续梁在荷载作用下,其实际变形曲线如图16.5(a)中的虚线所示。为计算梁的弯矩,可按以下步骤进行。

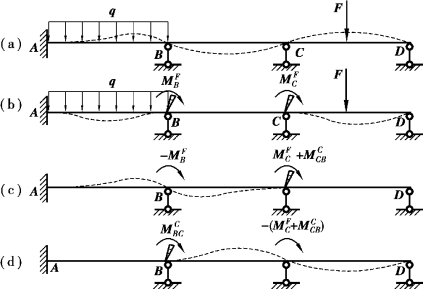
图16.5

在结点B,C处增设附加刚臂以限制结点B,C的转动。加上荷载,显然该梁在此种情形下仅在荷载作用下有变形,如图16.5(b)所示。此时,结点B,C的不平衡力矩分别为=。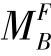

为了消除结点B,C处的两个不平衡力矩,在位移法中是令结点B,C同时产生与原结构相同的转角,也即同时放松两个结点,让它们一次就转到实际的平衡位置,如此就需要建立联立方程并求解它们,这是位移法的计算思路。在力矩分配法中则不是同时放松两个结点,而是逐次将各个结点轮流放松来达到同样的目的。

首先,放松结点B,此时结点C的附加刚臂仍然固锁,如图16.5(c)所示。显然这与前面介绍的单结点的情况完全相同,因此可按前述的方法来消除结点B处的不平衡力矩MFB。为此,需要先求出结点B处各杆端的分配系数。

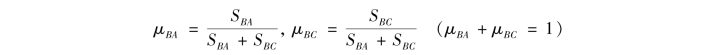
式中,SBA=4&BA,SBC=4&BC〔在图16.5(c)中,结点C被固锁了,因此杆BC的C端是固定端〕。

将结点B处的不平衡力矩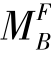反号进行力矩分配、传递。这样,结点B处便暂时获得了平衡。此时结点C上的不平衡力矩又新增加了,它是由结点B的分配弯矩传递而来的传递力矩。因而结点C上的不平衡力矩为。

其次,放松结点C,而将结点B固锁,如图16.5(d)所示。同样可按前述的方式来消除结点C处的不平衡力矩。结点B处各杆端的分配系数

式中,SCB=4&CB〔在图16.5(d)中,结点B被固锁了,因此杆BC的B端是固定端〕,SCD=3&CD。

将结点C处的不平衡力矩反号进行力矩分配、传递。这样结点C处也暂时获得了平衡,但此时,由于结点C的放松,CB杆的C端分配来的弯矩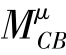将向其远端即B端传递,于是结点B处又重新产生了一个不平衡力矩。

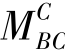再次,由于结点B处有了新的不平衡力矩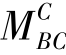,于是又将结点B放松,而将结点C固锁,按上述相同的方法进行分配、传递。如此循环往复地将各个结点轮流放松、固定,不断重复地进行力矩的分配和传递,那么不平衡力矩将会越来越小(这是因为分配系数和传递系数均小于1),直到传递弯矩小到足以满足计算精度要求而可略去时,即可停止计算。此时,经过各结点的逐次转动,就逐渐逼近了最后的平衡状态,即如图16.5(a)所示的情形。

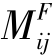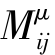最后,把以上计算过程中各杆杆端的固端弯矩、分配弯矩、传递弯矩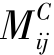对应叠加,就得到该杆端的最终弯矩。

综上所述,对于具有多个刚结点的连续梁和无侧移的刚架,用力矩分配法所得的结果是渐近解,因而该法属于渐近法。为了使计算的收敛速度较快,通常可从不平衡力矩较大的刚结点开始计算。

【例16.3】　试用力矩分配法计算如图16.6(a)所示的连续梁内力,并绘制弯矩图。已知各杆的抗弯刚度EI为常数。

【解】　①计算力矩分配系数。设,则。

刚结点B处:

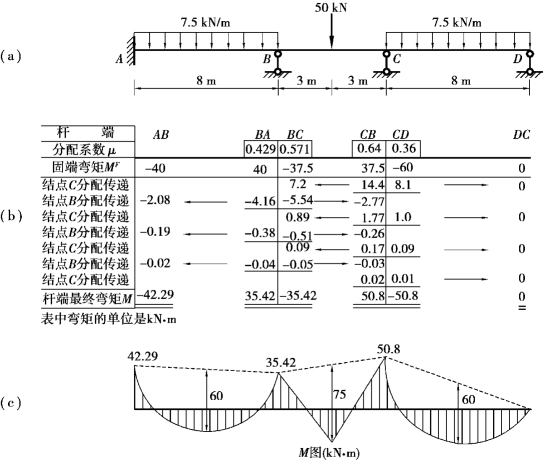
图16.6

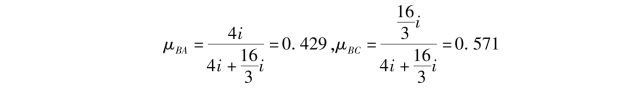
刚结点C处:

②计算固端弯矩。

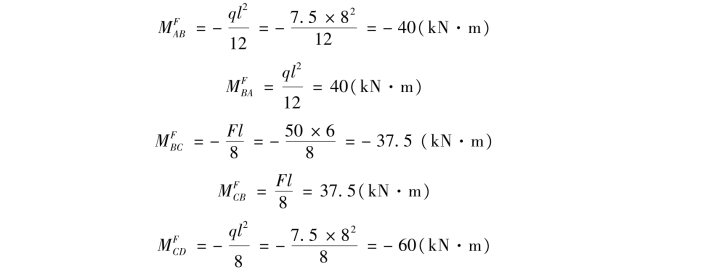
③轮流放松各结点,计算分配弯矩、传递弯矩。为了使计算收敛得更快,宜从不平衡力矩较大的结点开始,本例先放松结点C。最后叠加得各杆端最终弯矩,计算过程如图16.6(b)所示。

④根据计算结果画弯矩图,如图16.6(c)所示。

【例16.4】　试用力矩分配法计算如图16.7(a)所示连续梁内力,并绘出弯矩图。(www.xing528.com)

【解】　①该梁最右侧的外伸部分EF是静定的,其内力图可直接画出。因此,在后面的计算中可以不予考虑EF部分,进而可将作用在最右端F处的集中力平移至E点处,得到一个集中力和力偶,这样一来结点E即可化为铰支来处理,如图16.7(b)所示。

图16.7

②计算分配系数。为计算方便,设,则,如图16.7(b)所示。

刚结点B处:

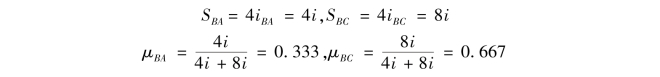
刚结点C处:

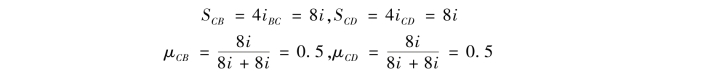
刚结点D处:

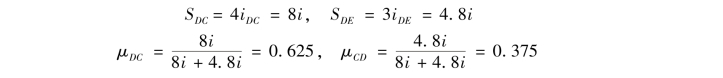
③计算固端弯矩。

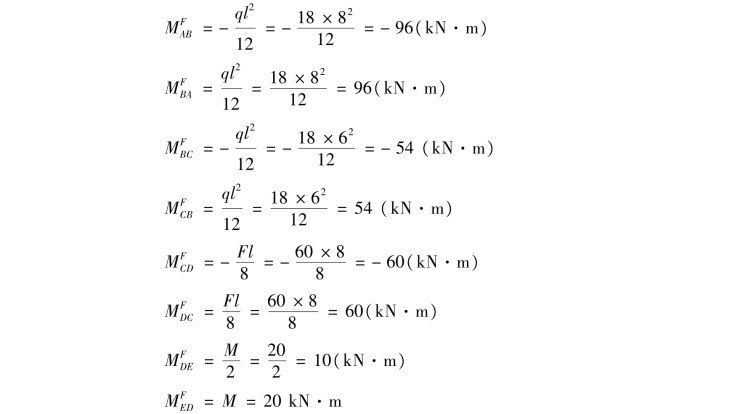
④轮流放松各结点,列表计算分配弯矩、传递弯矩,叠加得最终弯矩,计算过程如图16.7(c)所示。

本例先放松结点C。由于原图在结点C处作用有外力偶,为此必须要注意,在对结点C处的不平衡力矩进行分配时,用来分配的不平衡力矩应该是刚结点所连杆件近端的固端弯矩求和后反号再加上外力偶矩,作用在结点处的外力偶矩顺时针转向为正,逆时针转向为负。因此,在本例中,第一次放松结点C时,用来分配的不平衡力矩为

当结点C放松分配后,在放松结点B时,结点C要固锁,因此可同时放松结点D。由此可见,凡不相邻的各结点每次可同时放松,以便加快计算收敛的速度。

⑤根据计算结果画弯矩图,如图16.7(d)所示。

【例16.5】　试用力矩分配法计算如图16.8所示的刚架内力,并绘出弯矩图。

【解】　①计算分配系数。为计算方便,设,则。

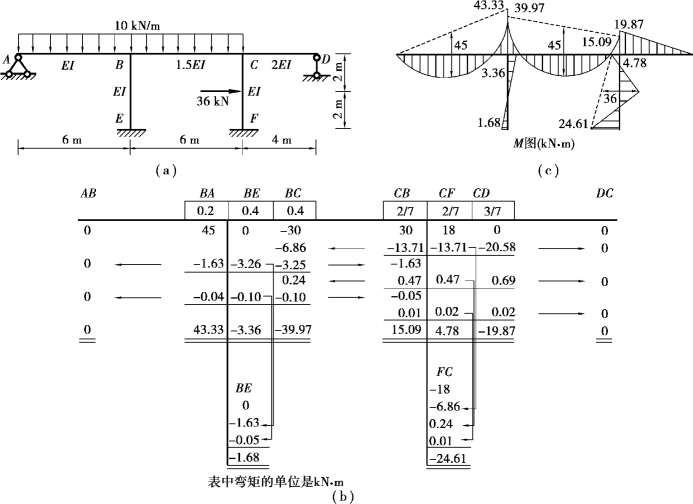
图16.8

刚结点B处:

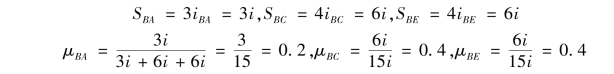
刚结点C处:

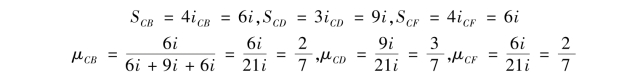
②计算固端弯矩。

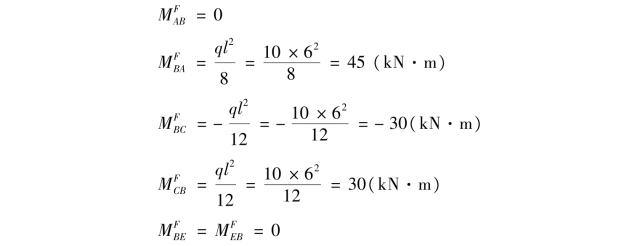
③轮流放松各结点,列表计算分配弯矩、传递弯矩,叠加得最终弯矩,计算过程如图16.8(b)所示。

④根据计算结果画弯矩图,如图16.8(c)所示。