力矩分配法在建筑力学中的基本概念

(1)转动刚度

如图16.1所示,当杆件AB的A端转动单位角位移时,A端(又称为近端)的弯矩MAB称为该杆端的转动刚度,用SAB表示,它反映了该杆端抵抗转动能力的大小。显然,转动刚度的大小不仅与杆件的线刚度有关,还与杆件的另一端(又称为远端)的支承情况有关。等截面直杆远端为不同约束时的转动刚度可以根据表15.1查得,如图16.1所示。

远端固定〔图16.1(a)〕　　　　　　　　SAB=4&

远端铰支〔图16.1(b)〕SAB=3&

远端定向支座〔图16.1(c)〕SAB=&

远端自由(或轴向支杆)〔图16.1(d)〕SAB=0

(2)传递系数

如图16.1所示,当A端(近端)转动时,B端(远端)也可能产生一定的弯矩,这就好比将近端的弯矩按一定的比例传递到了远端一样。因此将B端的弯矩MBA与A端的弯矩MAB之比称为由A端向B端的传递系数,用CAB表示,即

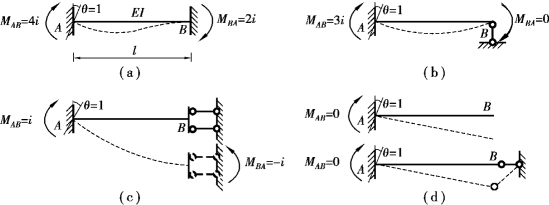
图16.1

由图16.1可知,等截面直杆的传递系数与远端的支承情况有关。

远端固定〔图16.1(a)〕　　　　　　　　CAB=0.5

远端铰支〔图16.1(b)〕CAB=0

远端定向支座〔图16.1(c)〕CAB=-1

远端自由(或轴向支杆)〔图16.1(d)〕CAB=0

(3)分配系数

如图16.2(a)所示刚架,在均布荷载和集中力作用下刚结点B产生角位移θB。假设在刚结点B处假想增设一附加刚臂,使刚结点B不能发生转动,我们把这一状态称为固定状态,如图16.2(b)所示。在固定状态下,由于各杆被约束隔离,可以独立分离出来研究,其内力可以直接查表15.1中载常数而计算得到,称为固端弯矩,用MF表示。同时结点B满足平衡条件,如图16.2(e)所示,据此可以求得附加刚臂的约束力矩,即

显然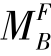是各固端弯矩所不能平衡的差值,所以又称为结点上的不平衡力矩。

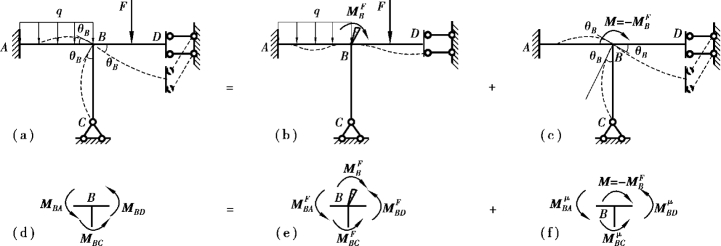
图16.2

为了保持结构受力不改变,在刚结点B处施加一个与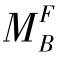大小相等转向相反的力矩M=-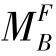,我们把这个状态称为放松状态,如图16.2(c)所示。根据叠加原理可知,该刚架的实际受力状态〔图16.2(a)〕等于固定状态〔图16.2(b)〕与放松状态〔图16.2(c)〕的叠加。

在放松状态下,刚结点B产生角位移θB,相当于各杆的B端都发生了转角位移θB。因此,在放松状态上各杆端弯矩为

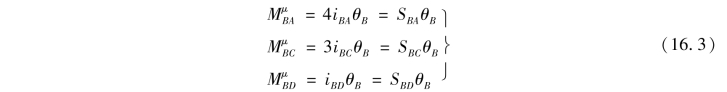(www.xing528.com)

同样,在放松状态下结点B也满足平衡条件,如图16.2(f)所示。

将式(16.3)代入式(16.4),有

于是有

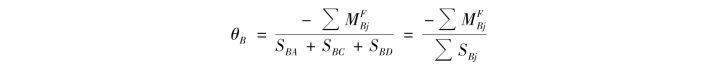
式中,表示相互于结点B处所有杆端的转动刚度之和。

将θB代回到式(16.3)中,可得

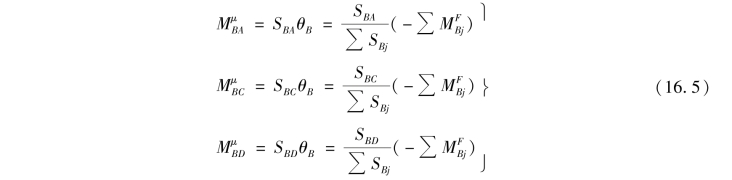
从式(16.5)可以看出,在放松状态下,作用在结点B上的反号不平衡力矩按各杆端的转动刚度(SBj)占结点B处所有杆端转动刚度之和(∑SBj)的比例分配给了汇互于结点B处的各杆端。我们把这个比例

称为分配系数,用μBj表示,即

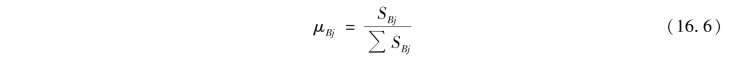
分配系数μBj表示将作用在结点B处的外力偶矩分配到各杆B端弯矩的比例,其中j可以是A,C,D等。

同一刚结点各杆端分配系数之间存在如下关系: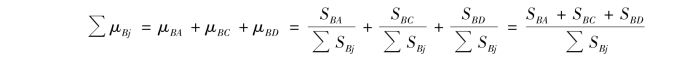

即

因此,同一结点处各杆端的分配系数之和等于1。

式(16.5)中的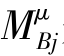是将作用在结点B处的外力偶矩按各杆端的分配系数μBj分配给各杆端得到的弯矩,因此将其称为分配力矩,于是有

于是式(16.5)可以改写为

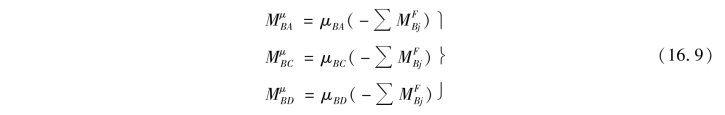
由式(16.9)可得到放松状态下各杆的近端力矩,而近端力矩将按各杆的传递系数传递给远端,于是有

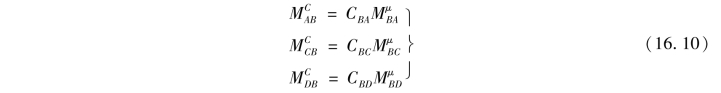
以上过程简称为“近端分配,远端传递”。