超静定结构的转角位移计算

下面以例题说明直接应用转角位移方程计算超静定结构的步骤。

【例15.3】　试用转角位移方程计算如图15.24(a)所示超静定刚架内力,并绘出弯矩图。

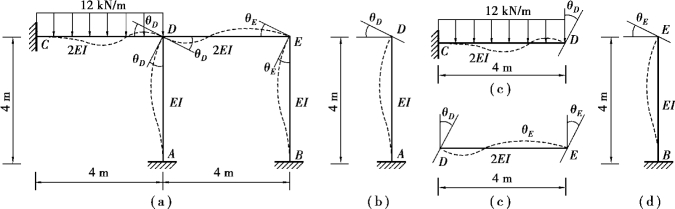
图15.24

【解】　①确定基本未知量。由图15.24(a)可知,由于A,B,C为固定支座,同时忽略杆件的轴向变形,因此该刚架有两个结点角位移:刚结点D处的转角θD和刚结点E处的转角θE,没有结点线位移。因此用位移法计算,此刚架有两个基本未知量θD,θE。

②列各杆端弯矩的转角位移方程。分别取各杆为隔离体,写出各杆端弯矩的转角位移方程。

为计算方便,令,于是有。

a.AD杆相当于两端固定的单跨超静定梁,其上无荷载作用,只有D端发生角位移θD,如图15.24(b)所示,因此AD杆两端截面的弯矩为

MAD=2&DAθD=2&θD

MDA=4&DAθD=4&θD

b.CD杆相当于两端固定的单跨超静定梁,其上作用有均布荷载,同时D端发生角位移,如图15.24(c)所示,因此,CD杆两端截面的弯矩为

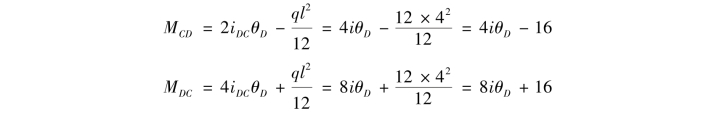
c.DE杆相当于两端固定的单跨超静定梁,其上无荷载作用,D端和E端分别发生角位移θD,θE,如图15.24(d)所示,因此DE杆两端截面的弯矩为

MDE=4&DEθD+2&DEθE=8&θD+4&θE

MED=2&DEθD+4&DEθE=4&θD+8&θE

d.BD杆相当于两端固定的单跨超静定梁,其上无荷载作用,只有E端发生角位移θE,如图15.24(e)所示,因此BE杆两端截面的弯矩为

MBE=2&BEθE=2&θE

MEB=4&EBθE=4&θE

③建立位移法方程。

a.取刚结点D为隔离体,如图15.25(a)所示,由静力平衡条件,有

图15.25

将前面求得的相应杆端弯矩代入上式,可得(www.xing528.com)

4&θD+8&θD+16+8&θD+4&θE=0

整理可得

20&θD+4&θE+16=0

b.取刚结点E为隔离体,如图15.25(b)所示,由静力平衡条件,有

将前面求得的相应杆端弯矩代入上式,可得

4&θD+8&θE+4&θE=0

整理可得

4&θD+12&θE=0

归纳即可得求解θD和θE的位移法方程,即

20&θD+4&θE+16=0

4&θD+12&θE=0

联解上述两个方程,可得

④计算各杆端的最终弯矩。将求解出的θD和θE代回到前面的杆端弯矩表达式,即可计算出各杆端的最终弯矩。

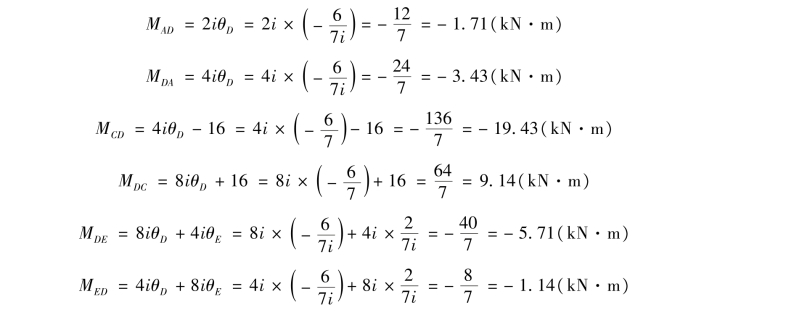
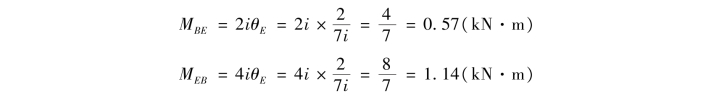
⑤画弯矩图。根据上面求出的各杆端最终弯矩即可绘出刚架的弯矩图,如图15.26所示。

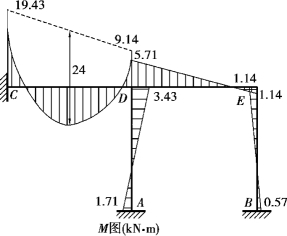
图15.26

本刚架的剪力图,同样可以先写出各杆端剪力与结点位移及荷载之间的关系表达式,即杆端剪力的转角位移方程,然后将由位移法方程求解出的结点位移代回到杆端剪力的转角位移方程,就可求得各杆端的最终剪力,并据此就可画出剪力图。

通过比较例15.2与例15.3的解题过程可以发现,应用转角位移方程所列出的位移法方程与前面所列出的位移法典型方程实质上是完全相同的,最终的计算结果也完全相同。