15个应用示例：建筑力学位移法

由上节介绍的位移法计算步骤可知,用位移法计算超静定结构的计算步骤与力法十分相似。下面通过例子来说明位移法的具体应用。

【例15.1】　试用位移法计算如图15.19(a)所示连续梁内力,并绘制其内力图。

【解】　①确定基本体系。此连续梁有两个刚结点B,C,无结点线位移。因此,基本未知量为B,C两结点角位移Z1,Z2。在B,C两刚结点处增加附加刚臂,并令两附加刚臂分别发生角位移Z1,Z2,得到如图15.19(b)所示的基本体系。

②建立位移法典型方程。

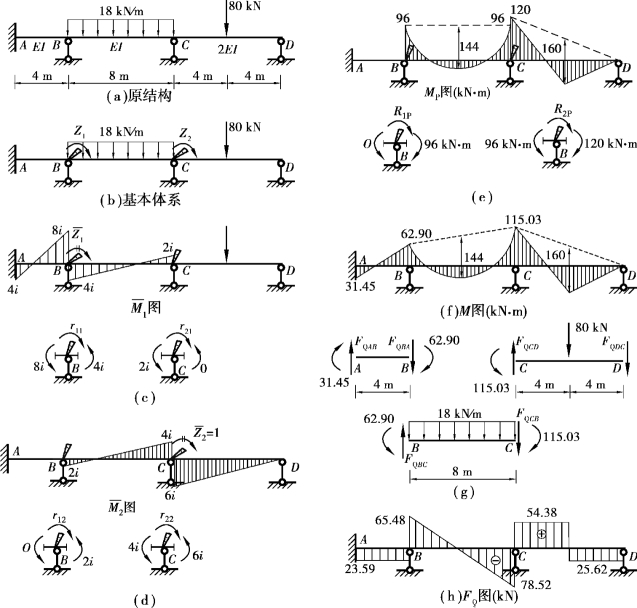
图15.19

r11Z1+r12Z2+R1P=0

r21Z1+r22Z2+R2P=0

③绘制图、图和MP图。由图15.19(a)可知各杆的线刚度互不相同。为计算方便,令

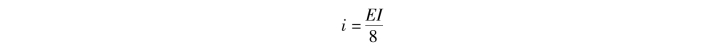
则

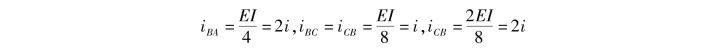
绘制的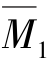图、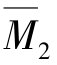图和MP图如图15.19(c)、(d)、(e)所示。

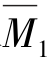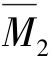④计算系数和自由项。从图、图和MP图分别截取结点B,C为隔离体,画出其受力图,如图15.19(c)、(d)、(e)所示。由各结点的力矩平衡方程可得

r11=8&+4&=12&,r22=4&+6&=10&

r12=r21=2&

R1P=-96kN·m,

R2P=96-120=-24kN·m

⑤解典型方程。将计算所得的系数和自由项代入典型方程可得

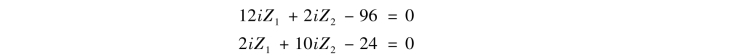
联解以上方程可得

⑥由叠加法M=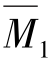Z1+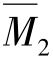Z2+MP求各杆端弯矩。

AB杆:

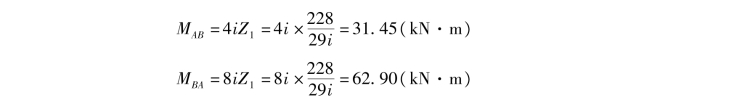
BC杆:(www.xing528.com)

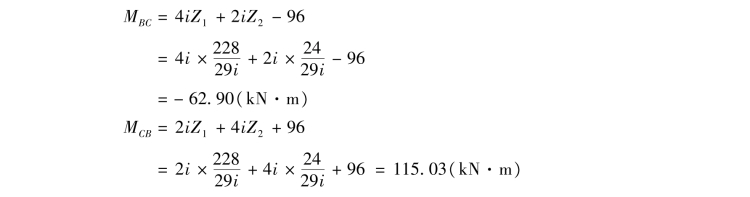
CD杆:

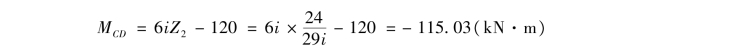
根据上面计算所得的各杆端弯矩绘制弯矩图,如图15.19(f)所示。

从图15.19(a)中分别截取杆AB、BC和CD为隔离体,由弯矩图可得各杆端力矩,各杆端剪力假设为正,画出三杆件隔离体的受力图,如图15.19(g)所示,由静力平衡条件求各杆端剪力,有

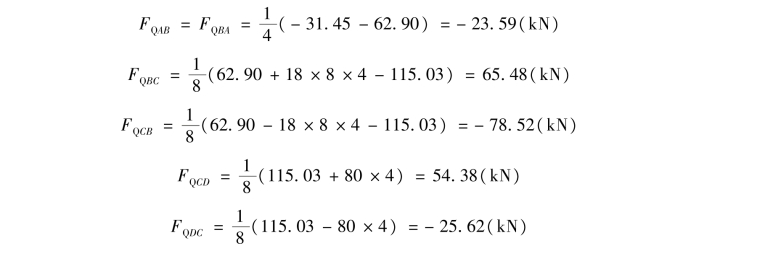
根据上述计算结果可绘出结构的剪力图,如图15.19(h)所示。

【例15.2】　试用位移法计算如图15.20(a)所示刚架内力,并绘制弯矩图。

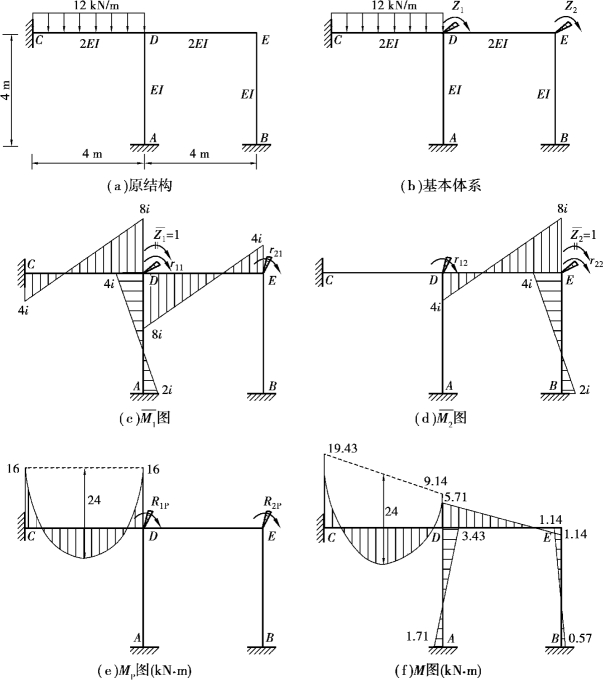
图15.20

【解】　①确定基本体系。此刚架有两个刚结点D和E,无结点线位移。因此,基本未知量为结点D和E处的角位移Z1和Z2,基本体系如图15.20(b)所示。

②建立位移法典型方程。

r11Z1+r12Z2+R1P=0

r21Z1+r22Z2+R2P=0

③令

,绘制基本结构在单位位移和荷载分别单独作用下的弯矩图图、图和MP图,分别如图15.20(c)、(d)、(e)所示。

④计算系数和自由项。在图15.20(c)、(d)、(e)中分别利用结点D,E的力矩平衡条件可计算出系数和自由项。

r11=8&+8&+4&=20&,r22=8&+4&=12&,r12=r21=4&,R1P=16kN·m,R2P=0

⑤解方程求基本未知量。将系数和自由项代入位移法方程,得

20&Z1+4&Z2+16=0

4&Z1+12&Z2=0

解方程得

⑥绘制弯矩图。由叠加公式计算各杆端弯矩值,绘出刚架的弯矩图,如图15.20(f)所示。

剪力的计算及剪力图的绘制可按前述方法进行,请读者自行计算。