位移法的典型方程与物理意义

如图15.13所示的刚架,杆件31和42有侧移发生,这类结构称为有侧移结构。经分析可知该刚架有一个独立的结点角位移Z1和一个独立的结点线位移Z2,共有两个基本未知量。在结点1处增加一附加刚臂,在结点2处增加一附加水平支座链杆(当然也可在结点1处增加一水平支座链杆),得到如图15.13(b)所示的位移法基本结构。

令附加刚臂产生与原结构相同的转角Z1,令附加链杆产生与原结构相同的线位移Z2,再将荷载加到基本结构上,如此便得到如图15.13(c)所示的位移法基本体系。在此必须强调,为了计算方便,所设的结点位移方向均按前述规定的正方向来假设,即结点角位移设为顺时针转向,结点线位移设为使整个杆件顺时针转动。

根据基本体系与原结构完全等效,即基本体系的变形和内力及反力与原结构完全相同。由于原结构在结点1和2处并无约束,也就没有反力偶和反力,因此基本结构在结点位移Z1,Z2和荷载共同作用下,附加刚臂的附加反力偶R1和附加支座链杆的附加反力R2都应该等于零,如图15.13(c)所示。

图15.13

设基本结构在结点位移Z1单独作用下引起的附加刚臂上的附加力偶为R11,引起的附加支座链杆的反力为R21,如图15.13(d)所示。

设基本结构在结点位移Z2单独作用下引起的附加刚臂上的附加力偶为R12,引起的附加支座链杆的反力为R22,如图15.13(e)所示。

设基本结构在荷载单独作用下引起的附加刚臂上的附加力偶为R1P,引起的附加支座链杆的反力为R2P,如图15.13(f)所示。

根据叠加原理,可得

R1=R11+R12+R1P=0

R2=R21+R22+R2P=0

再设基本结构在单位结点位移=1、=1分别单独作用下所引起的附加刚臂的附加反力偶分别为r11,r12,附加支座链杆的附加反力分别为r21,r22,如图15.14(a)、(b)所示。显然有

R11=r11Z1,R12=r12Z2,R21=r21Z1,R22=r22Z2

于是有

图15.14

式(15.2)称为位移法的典型方程,其物理意义是:基本结构在所有的结点位移和荷载共同作用下,每一个附加约束上的附加反力偶和附加反力都应等于零。因此,位移法典型方程实质上反映了原结构的静力平衡条件。

对于有n个独立结点位移的超静定结构,相应地在基本结构中应加入n个附加约束,根据每个附加约束的附加反力偶或附加反力均应等于零的平衡条件,即可建立n个方程。

在式(15.3)的典型方程中,主对角线上的系数r&&称为主系数或主反力,其他系数r&j(&≠j)称为副系数或副反力,R&P称为自由项。系数和自由项的正负号规定是:与该附加约束所设的位移方向一致为正,相反则为负。

主系数r&&表示基本结构在单位结点位移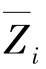=1单独作用下所引起的第&个附加约束的附加反力偶或附加反力,由于其方向总是与所设位移的方向一致,故主系数恒为正,且不会等于零。

副系数r&j表示基本结构在单位结点位移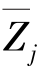=1单独作用下所引起的第&个附加约束的附加反力偶或附加反力,其值可能为正,可能为负,也可能等于零。另外,根据反力互等定理可知,位于主对角线两侧对称位置的两个副系数r&j与rj&是相等的,即r&j=rj&。

自由项R&P表示基本结构在荷载单独作用下所引起的第&个附加约束的附加反力偶或附加反力,其值可能为正,可能为负,也可能等于零。

在位移法的典型方程中,每个系数都是由单位结点位移所引起的附加约束的反力或反力偶。很明显,如果结构的刚度越大,那么这些反力或反力偶也就越大,因此这些系数又称为结构的刚度系数,位移法典型方程也称为结构的刚度方程,位移法也称为刚度法。

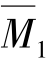为了求典型方程中的系数和自由项,可利用表15.1中所列出的形常数,绘出基本结构在单位结点位移分别单独作用下的弯矩图,即图、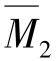图,如图15.15(a)、(b)所示;同样可利用表15.1中所列出的载常数,绘出基本结构在荷载单独作用下的弯矩图,即MP图,如图15.15(c)所示。

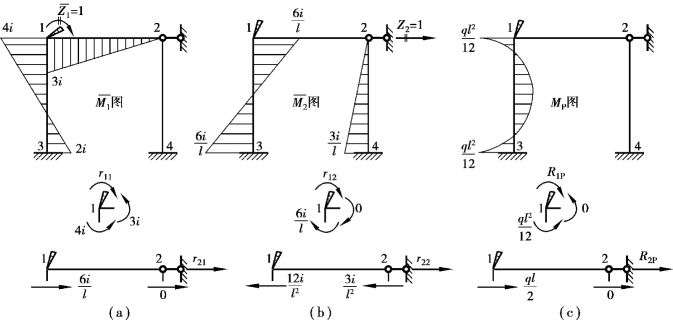
图15.15

位移法的系数和自由项计算可分为两类:一类是附加刚臂上的附加反力偶r11,r12和R1P;另一类是附加支座链杆的附加反力r21,r22和R2P。对于附加刚臂上的附加反力偶,可分别在图15.15(a)、(b)、(c)中取结点1为隔离体,由力矩平衡方程,可求得

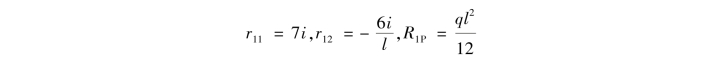
对于附加支座链杆上的附加反力,可分别在图15.15(a)、(b)、(c)中用截面截割两柱顶端,取柱顶端以上水平杆部分为隔离体,并由表15.1中查出柱13,24的顶端截面剪力,由投影方程,可求得

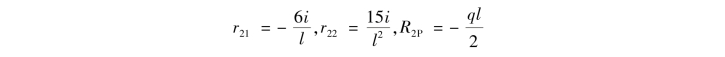(www.xing528.com)

将系数和自由项代入典型方程(15.3),有

解以上两个方程可得

所得结果为正值,说明结点1,2的实际位移方向与图15.13(c)中Z1,Z2所设的方向相同。

结构各杆端的最后弯矩可由叠加法求得。

结构的最后弯矩图如图15.16所示。

最后弯矩图的校核与力法中所述的校核方法相同。当确认弯矩图正确无误后,即可取隔离体并利用平衡条件计算出杆端的剪力和轴力。

从图15.13(a)中截取杆件12为隔离体,由如图15.16所示的M图可知杆端1的弯矩为,下侧受拉,杆端2截面的弯矩为0。画出杆12隔离体的受力图,杆端的剪力按正的方向假设,如图15.17(a)所示。由静力平衡方程,有

图15.16

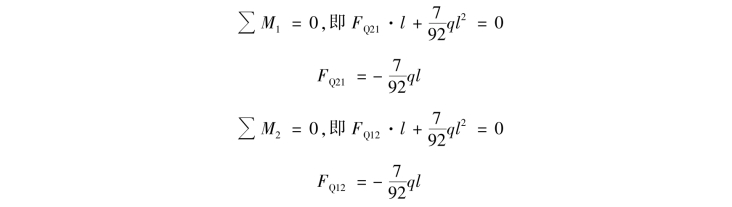
同理,从图15.13(a)中分别截取杆件13,24为隔离体,由图15.16得到各杆端弯矩,画出其受力图,杆端剪力均正方向假设,如图15.17(b)、(c)所示。由各杆的静力平衡条件,对于杆件13,有

图15.17

对于杆件24,有

由以上所求得的各杆端剪力给出结构的剪力图,如图15.17(d)所示。

由剪力图,根据静力平衡条件可求出各杆件的轴力,并画出轴力图。从图15.13(a)中分别截取结点1,2,由如图15.17(d)所示的剪力图得到各杆端的剪力,画出各结点的受力图,杆端轴力假设为正即拉力,如图15.18(a)、(b)所示。

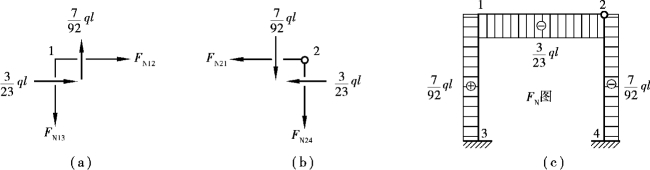
图15.18

对于结点1,由平衡方程,有

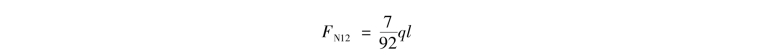
对于结点2,由平衡方程,有

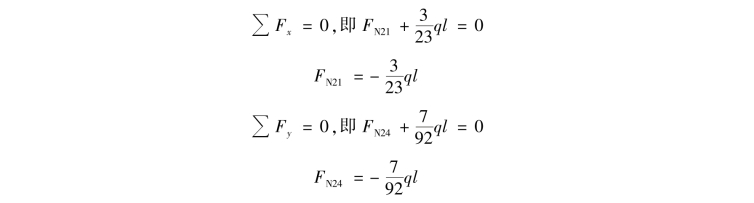
由以上计算出的各杆端轴力绘出结构的轴力图,如图15.18(d)所示。