如何用位移法计算连续梁结构的内力-建筑力学

下面我们以如图15.9(a)所示的连续梁为例,来说明如何用位移法计算超静定结构的内力。此连续梁只有一个刚结点,因此只有一个独立的结点角位移Z1,同时该连续梁中的各杆均没有侧移发生,此类结构称为无侧移结构,没有结点线位移。在结点B处增设一附加刚臂,便得到基本结构。由于附加刚臂限制了结点B的角位移,而原结构〔图15.9(a)〕中结点B是会产生角位移的,因此当荷载作用在基本结构上时,其位移和内力将与原结构不相同。如果令附加刚臂发生与原结构相同的角位移Z1,如图15.9(b)所示,那么二者的位移就完全相同了。将基本结构在荷载和独立的结点位移共同作用下的体系称为位移法的基本体系。

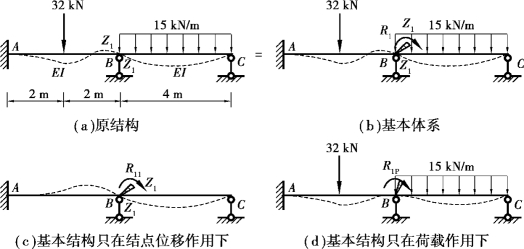
图15.9

就受力方面来说,基本结构中由于加入了附加刚臂,刚臂上将会产生附加反力偶R1(简称反力偶)。而原结构中并没有附加刚臂,当然也就不存在该反力偶。基本体系的位移与原结构的位移既然完全一致,其反力也就应完全相同。因此,基本结构在荷载和独立结点位移Z1共同作用下,附加刚臂上的反力偶R1必等于零,即

R1=0

设基本结构由Z1和荷载所引起的附加刚臂上的反力偶分别为R11和R1P,如图15.9(c)、(d)所示,根据叠加原理,则有

R1=R11+R1P=0

设基本结构在单位结点位移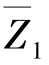=1单独作用下所引起的附加刚臂的反力偶为r11,如图15.10(a)所示,则R11=r11Z1,于是有

式(15.1)就是求解基本未知量Z1的位移法基本方程。

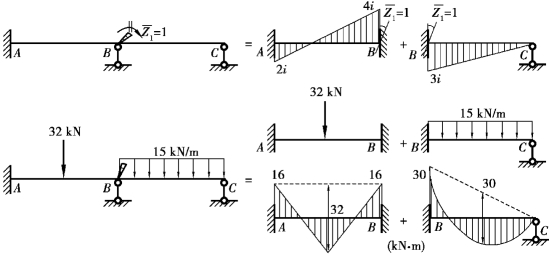
图15.10

由式(15.1)可知,要确定Z1,应先求出r11和R1P,因基本体系中各杆均可视为单跨超静定梁,如图15.10所示。

因此,可利用表15.1中的第1,3栏计算简图的杆端弯矩,绘出基本结构在单位结点位移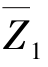=1单独作用下的弯矩图,如图15.11(a)所示的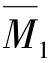图;利用表15.1中的第8,10栏计算简图的杆端弯矩,绘出基本结构在荷载单独作用下的弯矩图,如图15.11(b)所示的MP图。

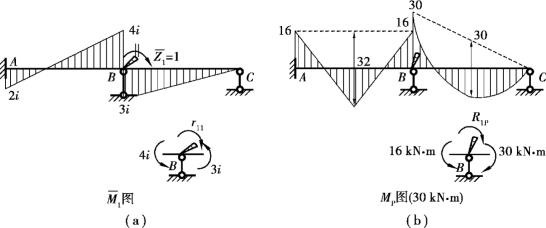
图15.11

由图,取结点B为隔离体,如图15.11(a)所示,根据力矩平衡条件,可得

r11=4&+3&=7&(www.xing528.com)

式中,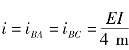是BA杆和BC杆的线刚度。

同样,由MP图,取结点B为隔离体,如图15.11(b)所示,根据力矩平衡条件0,可得

R1P=16kN·m-30kN·m=-14kN·m

将r11和R1P的计算结果代入位移法基本方程(15.3),可解得

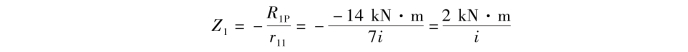
Z1的计算结果为正,表示Z1的方向与图15.11(b)中所设的方向相同。

结构的最后弯矩图可由叠加法绘制。

BA杆B端截面上的弯矩为

MBA结果为正表示BA杆B端截面上的弯矩的方向为绕杆端顺时针转动,即上侧受拉。

BC杆B端截面上的弯矩为

MBC结果为负表示该BC杆B端截面上的弯矩的方向为绕杆端逆时针转动,即上侧受拉。

根据以上计算结果绘出该连续梁的最后弯矩图,如图15.12所示。

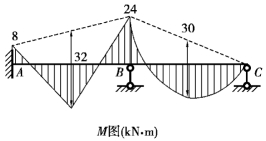
图15.12

上面以一个简单的例子讨论了位移法的基本原理,为了更进一步理解位移法的求解方法,下面用一个有侧移的刚架来说明位移法的典型方程和解题步骤。