(1)位移法基本未知量的确定
由前述的讨论可知,如果结构上的每根杆件两端的角位移和线位移均已求得,那么所有杆件的杆端内力就都可以由形常数和载常数确定。因此,在位移法中,基本未知量应该是各杆件的位移即结点位移。在应用位移计算时,应首先确定独立的结点角位移和线位移。
确定独立的结点角位移比较简单。根据刚结点的特点可知,在同一刚结点处各杆端的转角相等,因此每一个刚结点只有一个独立的结点角位移。在固定支座处,其转角等于零或者是已知的位移,不能作为结点角位移未知量;铰支座和铰结点各杆端的转角并不是独立的,在确定杆端的内力时可以不需要它们的数值,因此也不能作为结点角位移未知量。所以,确定结构独立的结点角位移时,只需要知道刚结点的数目即可。如图15.5(a)所示刚架,有两个刚结点,因此其独立的结点角位移有2个。
确定独立的结点线位移数目时,一般情况下每个结点都可能有水平位移和竖向位移两个线位移。但对于受弯杆件通常略去其轴向变形,并只考虑微小的弯曲变形,因而可以认为受弯直杆两端之间的距离在变形前后保持不变,这样每一根受弯直杆就相当于一个约束,从而减少了独立的结点线位移数目。如图15.5(a)所示的刚架,A,B,C三个固定支座均无任何位移,三根柱子的长度保持不变,因而结点1,2,3便都没有竖向线位移。同样由于两根水平杆的长度也保持不变,因而结点1,2,3的水平位移相同。由此可知,该刚架只有一个独立的结点线位移。
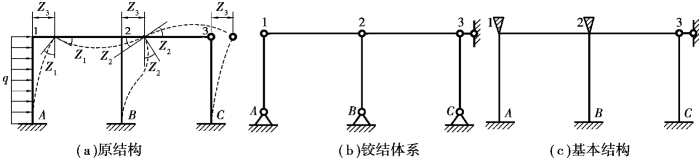
图15.5
确定独立的结点线位移还可用如下方法:由于每根杆件都可能有水平和竖向两个线位移,而每根受弯直杆提供一个两端距离不变的约束,可以假设将原结构中的所有刚结点和固定支座都改为铰结点或铰支座,而得到一个相应的铰结体系。如果此铰结体系为几何不变体系,则原结构所有结点都没有线位移;如果相应的铰结体系为几何可变或瞬变体系,那么,我们最少需要增加几根支座链杆才能使其成为几何不变体系,所需要增加的最少链杆数目就是原结构独立的结点线位移数目。如图15.5(a)所示刚架,其相应的铰结体系如图15.5(b)所示,显然这是一个几何可变体系,必须在某结点处增加至少一根非竖向的链杆才能成为几何不变体系,因此可知原结构有一个独立的结点线位移。
(2)位移法的基本结构
由位移法的基本思路可知,用位移法计算超静定结构时,每根杆视为一根单跨超静定梁,因而位移法的基本结构就是将每根杆件都暂时变为两端固定或一端固定一端铰支的单跨超静定梁。为此,可假想地在每个刚结点上加上一个附加刚臂,以阻止刚结点的转动(应注意:附加刚臂只能限制结点的转动而不能限制其移动),同时假想地在每一个有独立结点线位移的方向加上附加支座链杆以阻止结点线位移。
如图15.5(a)所示的刚架,在两刚结点1,2处分别加上附加刚臂,并在结点3处加一根水平方向的附加支座杆,这样原结构中的A1杆、12杆、B2杆就成为两端固定,而23杆、C3杆成为一端固定一端铰支的单跨静定梁,如图15.5(c)所示,这即是原结构的位移法基本结构,它是由单跨超静定梁形成的组合体。(https://www.xing528.com)
如图15.6(a)所示刚架,有4个刚结点,所以有4个独立结点角位移。将所有固定支座变成铰支座,将刚结点变成铰结点后,体系为几何可变体系,至少需要增加两根水平方向的链杆才能成为几何不变体系〔图15.6(b)〕,所以该刚架有2个独立的结点线位移。在每一个刚结点处增加附加刚臂,在结点4、结点5处增加水平方向的附加链杆,即得到该刚架位移法的基本结构,如图15.6(c)所示。
如图15.7(a)所示的刚架,经过分析可知有4个独立的结点角位移(注意:其中结点4也是刚结点,即杆件34和杆件54在该处刚结),2个独立的结点线位移,共有6个基本未知量。增加4个附加刚臂和2根附加链杆后,即可得到如图15.7(b)所示的基本结构。
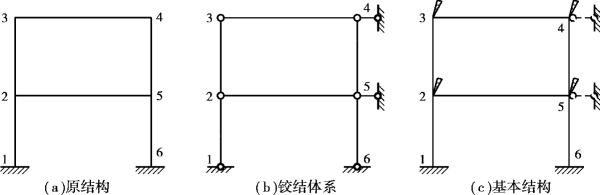
图15.6

图15.7
在确定独立的结点线位移时,必须要注意上述的确定方法是以受弯直杆变形后两端的距离保持不变为前提的。对于需要考虑轴向变形的链杆(EA≠∞),如图15.8(a)所示;或对于受弯曲杆,如图15.8(b)所示,则其两端的距离不能视为保持不变。因此,如图15.8(a)、(b)所示的结构,其独立的结点线位移应该是2个而不是1个。
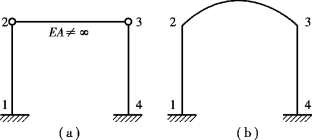
图15.8
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




