建筑力学（第2版）：支座移动超静定计算结果为

对于静定结构,支座移动时将使其产生位移而不会产生内力和反力,如图14.28(a)所示的静定梁,支座B有位移ΔB,沉降到B1,此时AB杆可绕A端和B端自由转动,AB杆只发生刚性位移,AB轴线保持为直线,没有产生变形,也就不会产生内力,也不会产生反力。而对于如图14.28(b)所示的超静定梁情况就有所不同了,同样是支座B有位移ΔB,沉降到B1,但由于A端是固定支座,AB杆不能绕A支座自由转动会而产生弯曲变形,由此就会产生内力,同时也会产生支座反力。

图14.28

用力法计算支座移动时超静定结构的内力,其原理与超静定结构在荷载作用下的计算类似,唯一的区别在于典型方程中的自由项不同。

如图14.29(a)所示超静定刚架,设支座B由于某种原因产生了水平位移a、竖向位移b及转角φ。选取如图14.29(b)所示的基本结构。根据基本结构在所有多余未知力和支座移动共同作用下,沿多余未知力方向的位移应与原超静定结构相应的位移相等的条件,可建立典型方程如下

δ11X1+δ12X2+δ13X3+Δ1c=0

δ21X1+δ22X2+δ23X3+Δ2c=-φ

δ31X1+δ32X2+δ33X3+Δ3c=-a

各方程中等号右边分别为原超静定结构中与X1,X2,X3方向对应的位移,φ,a前的负号是因为实际位移方向与所设的多余未知力X2,X3方向相反。典型方程中系数与支座移动无关,其计算方法同前。自由项Δ1c,Δ2c,Δ3c分别表示基本结构由于支座移动所引起的沿多余未知

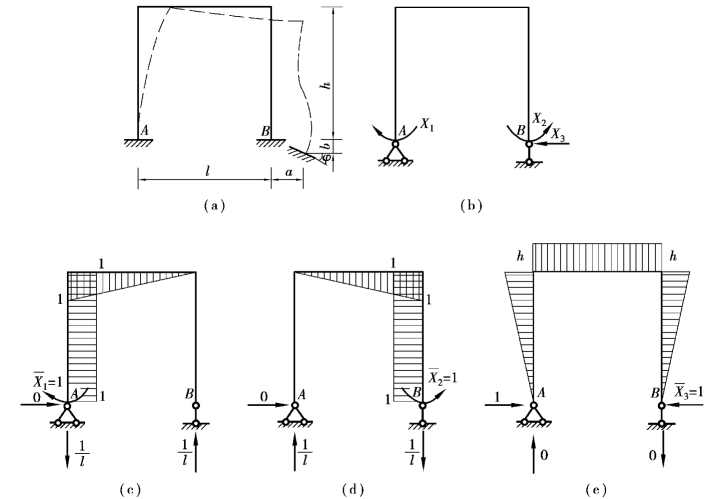
图14.29

力X1,X2,X3方向的位移,可按静定结构由于支座移动所引起的位移计算公式计算

式中,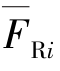为基本结构在单位多余未知力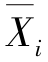=1单独作用下所产生的支座反力;c为与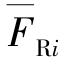相对应的支座位移,支座位移与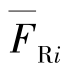方向相同乘积为正,相反则乘积为负。由如图14.29(c)、(d)、(e)所示的虚拟反力,可得

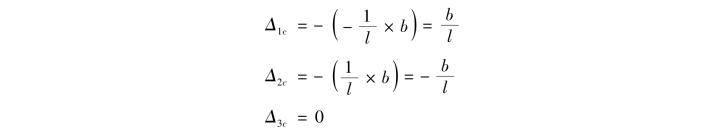
将求出的系数和自由项代入典型方程,即可求解出多余未知力X1,X2,X3。因为基本结构是静定结构,支座移动并不会使其产生内力,因此最后内力只是由多余未知力所引起,即(www.xing528.com)

【例14.8】　如图14.30(a)所示为两端固定的单跨超静定梁,支座A顺时针转动了角位移φ。试用力法计算内力,并绘制内力图。

【解】　取如图14.30(b)所示的简支梁为基本结构,因X3=0(参见例14.1),因此只需求解两个多余未知力,典型方程为

δ11X1+δ12X2+Δ1c=φ

δ21X1+δ22X2+Δ2c=0

绘出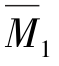图、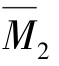图如图14.30(c)、(d)所示。由图乘法求得各系数为

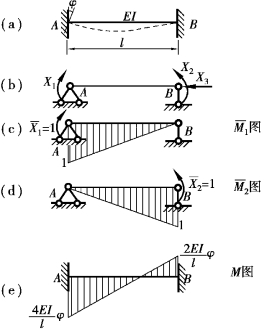
图14.30

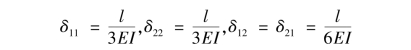
自由项Δ1c,Δ2c代表基本结构由于支座位移引起的沿X1,X2方向的位移。由于我们在取基本结构时已将发生转角的固定支座A改为铰支座,故支座A的转动已不再对基本结构产生任何影响,所以有

Δ1c=Δ2c=0

如按公式可得到同样的结果。

将系数、自由项代入典型方程可解得

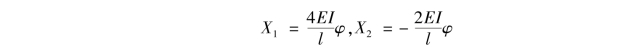
根据叠加公式绘出最后弯矩图,如图14.30(e)所示。