对称结构计算简化方法：应用于建筑力学

(1)选取对称的基本结构

计算对称结构时,应考虑选取对称的基本结构。如图14.17(a)所示的三次超静定刚架,可从横梁中点对称轴处切开,选取如图14.17(b)所示的基本结构。横梁的切口两侧有三对大小相等而方向相反的多余未知力,其中X1,X2为正对称的多余未知力,X3为反对称的多余未知力。根据基本结构在切口处相对位移为零的条件,建立力法方程为

显然在对称的基本结构上由正对称的单位多余未知力=1,=1所产生单位弯矩图〔图14.17(c)〕,图〔图14.17(d)〕及相应的变形是正对称的;而基本结构由反对称的单位多余未知力=1所产生的单位弯矩图图〔图14.17(e)〕及相应的变形是反对称的。用图乘法计算力法典型方程中的系数时,由于正、反对称的两图相乘的结果必然为零,因此有

图14.17

于是,典型方程便简化为

可以看出,典型方程被分为两组:一组是只包含正对称多余未知力X1,X2的二元一次方程组;另一组是只包含反对称多余未知力X3的一元一次方程。由此说明,在用力法计算对称结构时,只要选取对称的基本结构,正对称多余未知力的单位弯矩图与反对称多余未知力的单位弯矩图之间图乘所得的副系数必等于零;同时典型方程组将由高阶方程组降为两个低阶方程组,从而使计算系数和解算方程的工作得以简化。

下面进一步讨论对称结构在正对称荷载和反对称荷载作用下的简化计算。

(2)对称结构在正对称荷载作用下的特点

如图14.18(a)所示,当对称结构受正对称荷载作用时,选取对称的基本结构,则基本结构在荷载作用下所引起的弯矩图MP及相应变形的也是正对称的。因此

图14.18

代入典型方程式,则有

X1≠0,X2≠0,X3=0

最后的弯矩为

显然最后的弯矩图将是正对称的。由此可推知,此时结构的所有反力、内力和位移都将是正对称的。结构的弯矩图和轴力图是正对称的,而剪力图是反对称的(这是由于剪力的正负规定所致,而剪力的实际方向是正对称的)。

(3)对称结构在反对称荷载作用下的特点

如图14.19(a)所示,当对称结构受反对称荷载作用时,同样选取对称的基本结构,则基本结构在荷载作用下所引起的弯矩图MP及相应变形的也是反对称的。因此有

Δ1P=0,Δ2P=0,Δ3P≠0(www.xing528.com)

代入典型方程式可得

X1=X2=0,X3≠0

图14.19

最后的弯矩为

显然最后的弯矩图将是反对称的。由此可推知,此时结构的所有反力、内力和位移都将是反对称的。结构的弯矩图和轴力图是反对称的,而剪力图是正对称的(剪力的实际方向是反对称的)。

(4)对称结构在非对称荷载作用下的简化计算

当对称结构承受非对称荷载作用时,我们可以将荷载分解为正、反对称两组,将它们分别作用于结构上求解,然后将计算结果叠加,如图14.20所示。

显然,若取对称的基本结构进行计算,则在正对称荷载作用下将只有正对称的多余未知力,反对称荷载作用下只有反对称的多余未知力。

图14.20

【例14.5】　利用结构的对称性,试用力法计算如图14.21(a)所示刚架内力,并绘制弯矩图。

图14.21

【解】　此结构为三次超静定对称刚架,荷载是非对称的。将荷载分解为正对称荷载及反对称荷载两种情况,分别如图14.21(b)、(c)所示。在正对称荷载作用下〔图14.21(b)〕,如果忽略横梁的轴向变形,则只有横梁承受大小为F/2的轴向压力,其他杆件没有内力。故原结构的弯矩都是由反对称荷载〔图14.21(c)〕引起的,所以只需要对反对称荷载作用的情况进行计算。

选取如图14.21(d)所示的对称基本结构,由于荷载是反对称的,只有反对称多余未知力X1,建立典型方程为

δ11X1+Δ1P=0

分别绘出基本结构在=1及荷载作用下的弯矩图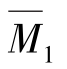图和MP图,分别如图14.21(e)、(f)所示。由图乘法计算系数和自由项为

将以上系数和自由项代入力法方程,解得

根据叠加法,绘出弯矩图,如图14.21(g)所示。