超静定梁和刚架在荷载下的内力计算方法

梁和刚架是以弯曲变形为主的结构,力法典型方程中的各系数和自由项可按下列公式计算:

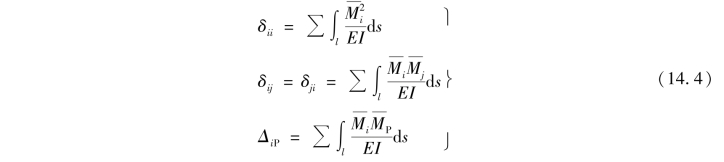
【例14.1】　如图14.10(a)所示为两端固定的超静定梁,受均布荷载q的作用,试用力法计算内力,并绘制内力图。

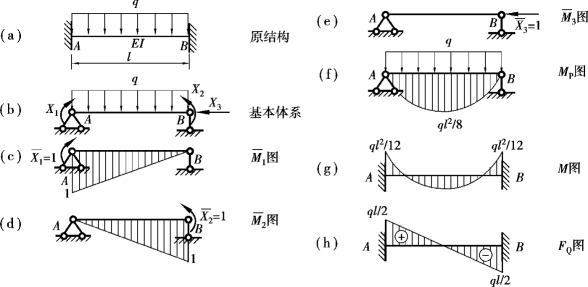
图14.10

【解】　①选取基本结构。这是一个三次超静定梁,可去掉A,B端的转动约束和B端的水平约束,代之以多余未知力X1,X2,X3,得到如图14.10(b)所示的基本体系。

②建立力法方程。

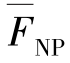基本结构的各图和MP图如图14.10(c)~(f)所示。由于=0,由位移计算或图乘法可知δ13=δ31=0,δ23=δ31=0,Δ3P=0。因此典型方程的公式变换为

δ33X3=0

在计算δ33时,若同时考虑弯矩和轴力的影响,则有

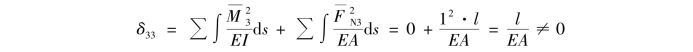
于是有

X3=0

这表明两端固定的梁在垂直于梁轴线的荷载作用下并不产生水平反力,因而此超静定梁可简化为只需求解两个多余约束的问题,典型方程简化为

δ11X1+δ12X2+Δ1P=0

δ21X1+δ22X2+Δ2P=0

③计算系数和自由项。分别绘出基本结构在单位多余未知力和作用下的弯矩图,即图,图〔图14.10(c)、(d)〕,以及荷载作用下的弯矩图MP图〔图14.10(f)〕,利用图乘法计算方程中各系数和自由项。由图自乘,可得

由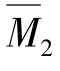图自乘,可得

由图与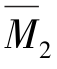图互乘,可得

由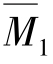图与MP图互乘,可得

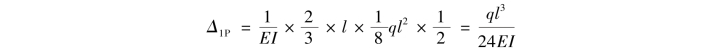
由图与MP图互乘,可得

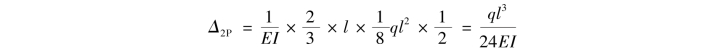
④解方程求多余未知力。将求得的系数和自由项代入力法方程,化简后得到

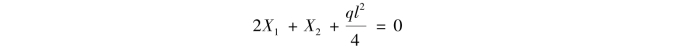
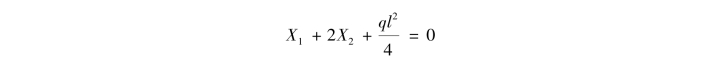(www.xing528.com)

由此解得

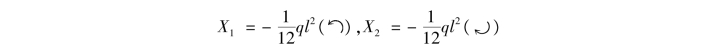
负号表示X1,X2的实际方向与假设的方向相反,即X1逆时针转向,X2为顺时针转向。

⑤绘制内力图。本题中由于已求出A,B两端截面上的弯矩,故用区段叠加法绘出原结构的弯矩图,如图14.10(g)所示。

绘剪力图时,可以取杆件为隔离体,利用已知杆端弯矩,由静力平衡条件,求出杆端剪力,然后绘出原结构的剪力图,如图14.10(h)所示。

由以上计算可知,单跨超静定梁的弯矩图与同跨度、同荷载的简支梁相比较,因超静定梁两端受多余约束限制,不能产生转角位移而出现负弯矩(上侧受拉),故梁中点处的弯矩值较相应简支梁减少,降低了最大内力峰值,使整个梁上内力分布得以改善。

【例14.2】　试用力法计算如图14.11(a)所示超静定刚架内力,并绘制内力图。

图14.11

【解】　①选取基本结构。此刚架为二次超静定结构,去掉B支座处的两个约束,代之以相应的多余未知力X1,X2,得到如图14.11(b)所示的基本体系。

②建立力法方程。由基本结构在多余未知力X1,X2及荷载共同作用下,B支座处沿X1,X2方向上的位移分别为零的位移条件,建立力法方程为

δ11X1+δ12X2+Δ1P=0

δ21X1+δ22X2+Δ2P=0

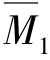③计算系数和自由项。分别绘出基本结构在单位多余未知力作用下的图,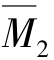图〔图14.11(c)、(d)〕,以及在荷载作用下的MP图〔图14.11(e)〕,利用图乘法计算方程中各系数和自由项。由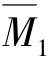图自乘,可得

由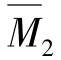图自乘,可得

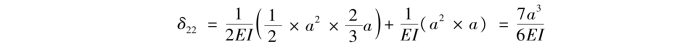
由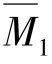图与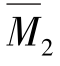图互乘,可得

由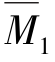图与MP图互乘,可得

由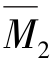图与MP图互乘,可得

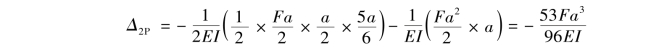
④解方程求多余未知力。将以上各系数和自由项代入力法方程,消去后得

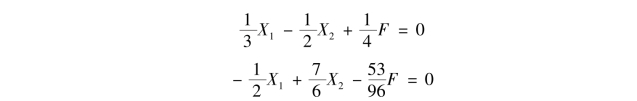
联立解得

负号表示X1的实际方向与假设的方向相反,即X1向左。

⑤绘制内力图。利用叠加公式,计算控制截面A,C上的弯矩值,绘出弯矩图如图14.11(f)所示。根据静定结构分析方法,由静力平衡条件,绘出剪力图和轴力图分别如图14.11(g)、(h)所示。