静定结构位移计算|建筑力学

如果要求结构只受荷载作用下K点沿指定方向的位移ΔKP。ΔKP有两个下标:第一个下标K表示该位移的位置和方向,即K点沿指定方向的位移;第二个下标P表示引起该位移的原因,即是由荷载引起的。此时由于支座没有移动,式(13.3)中的()为零,则其位移计算的一般公式为

在讨论结构在荷载作用下的位移计算时,仅限于研究线弹性结构,即结构的位移与荷载成正比,因而荷载对位移的影响就可以叠加,而且当荷载全部卸除后位移也完全消失。这样的结构,位移应是微小的,应力与应变的关系符合胡克定律。因此,如图13.7(b)所示,实际状态下各微段由内力FNP和MP分别引起的轴向变形和弯曲变形分别为

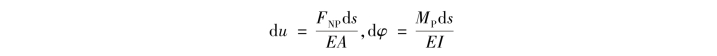
式中,E为材料的弹性模量,A和I分别为杆件截面的面积和惯性矩。实际状态下各微段由内力FQP引起的剪切变形为

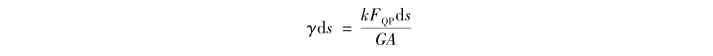
式中,G为剪切弹性模量;k为切应力沿截面不均匀分布而引入的修正系数,其值也与截面形状有关,对于矩形截面k=1.2,对于圆形截面k=1.11。

将微段变形代入式(13.4),得

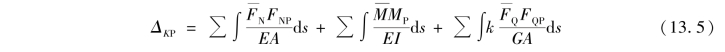
式(13.5)就是杆系结构在荷载作用下的位移计算公式。式(13.5)右边三项分别代表结构的轴向变形、弯曲变形和剪切变形对所求位移的影响。在实际计算中,根据结构的具体情况,常常可以只考虑其中的一项(或两项),以进一步简化位移计算。

(1)梁和刚架在荷载作用下的位移计算

对于梁和刚架,其位移主要由弯矩引起,轴力和剪力的影响很小,可以略去,因此梁和刚架的位移计算公式可简化为

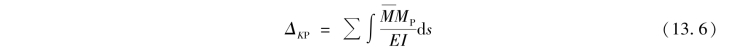
(2)桁架在荷载作用下的位移计算

理想桁架只受结点荷载作用,桁架中的每一根杆件只有轴力作用,没有剪力和弯矩,而且同杆件的轴力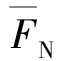,FNP以及轴向刚度EA沿杆长l均为常数,因此桁架在荷载作用下的位移计算可以简化为

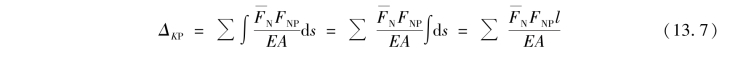
(3)组合结构在荷载作用下的位移计算

组合结构由梁式杆和桁架杆组成,对于其中的梁式杆只考虑弯矩M的影响,桁架杆只考虑轴力FN影响,因此组合结构在荷载作用下的位移计算可简化为

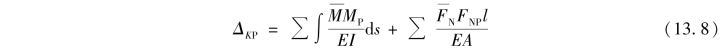
【例13.1】　如图13.9(a)所示的简支梁,受均布载q作用,抗弯刚度为EI。试求截面B的转角θB。

【解】　①因为拟求的位移是截面B的转角,因此在梁的B点加一单位集中力偶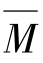=1作为虚拟状态,如图13.9(b)所示。

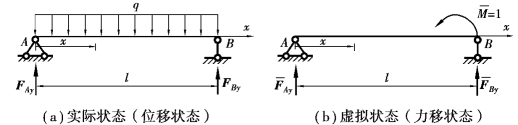
图13.9

②分别列出实际状态和虚拟状态的弯矩方程MP(x),(x)。由静力平衡条件分别求出两种状态下的支反力。

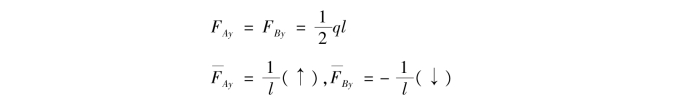
建立如图所示的x坐标,则有

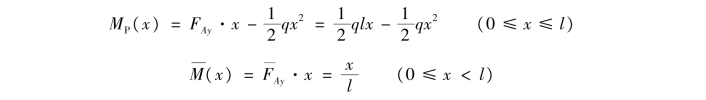(www.xing528.com)

③将MP(x),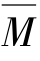(x)代入式(13.6),得

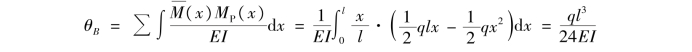
【例13.2】　一静定平面刚架各杆的抗弯刚度和所受荷载如图13.10(a)所示,试求刚架上C点的竖向位移ΔCy。

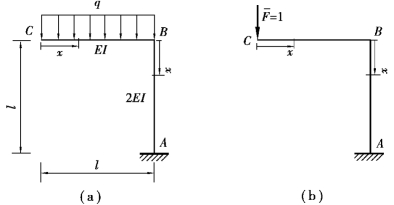
图13.10

【解】　①因需求C点的竖向位移ΔCy,故在C点加竖向单位荷载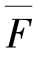=1作为虚拟状态,如图13.10(b)所示。

②分别列出各杆的,MP方程。

CB杆:以C点为坐标原点,x坐标向右为正向。

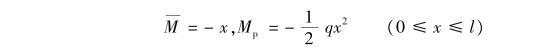
BA:以B点为坐标原点,x坐标向下为正向。

③计算位移。因结构由CB杆及BA杆组成,故应对各杆分别进行积分再求和。

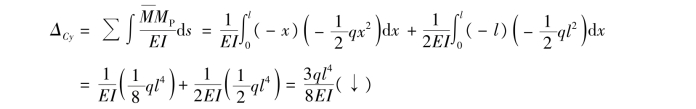
【例13.3】　如图13.11(a)所示桁架,各杆件的截面面积均为A=1cm2,弹性模量E=210GPa。试求结点C的竖向位移ΔCy。

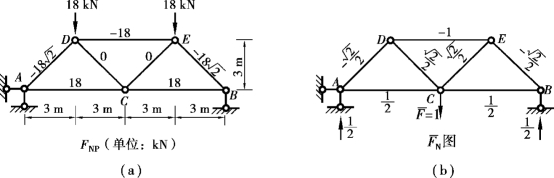
图13.11

【解】　①为求C点的竖向位移,在C点加一竖向单位力,并求出=1引起的各杆轴力,如图13.11(b)所示。

②求出实际状态下各杆的轴力FNP,如图13.11(a)所示。

③将各杆轴力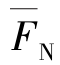,FNP及其长度列入表13.1中,再运用公式进行运算。

表13.1　桁架位移计算

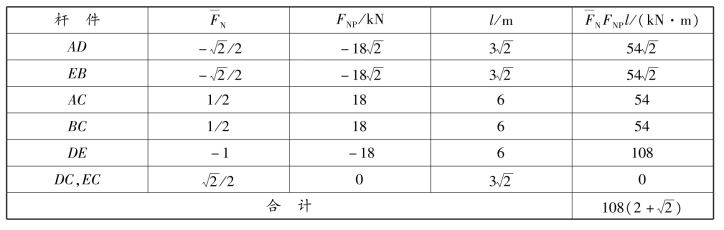
因为该桁架是对称的,所以由式(13.7)得

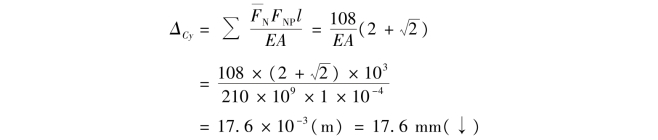
计算结果为正,说明C点的竖向位移与假设的单位力方向相同,即竖直向下。

如果桁架中有较多的杆件内力为零计算较为简单时,不用列表,可直接代入公式进行计算。