实功与虚功：力的功及其作用点位移

(1)功的概念

力在其作用点位移上的积累效应称为力的功。恒力做的功等于力的大小与作用点位移的乘积。如图13.4所示,设物体上A点受到恒力F的作用时,从A点移到A′点,发生了Δ的线位移,则力F在发生位移Δ的过程中所做的功为

式中,θ为力F与线位移Δ之间的夹角。功是标量,它的量纲为力乘以长度,其单位用N·m或kN·m表示。当力与其作用点的位移方向相同时,力做正功,反之则做负功。

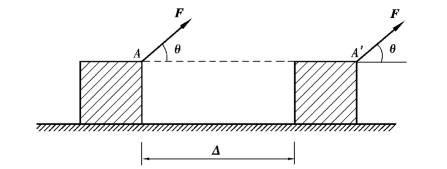
图13.4

(2)实功与虚功

力在由其本身原因所引起的作用点位移上所做功称为实功。而力在由其他原因所起的位移上所做的功称为虚功。

如图13.5(a)所示简支梁,在静力荷载F1的作用下发生了如图中虚线所示的变形,达到平衡状态。当F1由零逐渐缓慢地加到其最终值时,其作用点沿F1方向产生了位移Δ11,由于Δ11是由F1所引起的位移,所以F1沿Δ11所做的功是实功,用W11表示。(www.xing528.com)

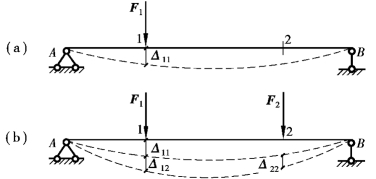
图13.5

弹性结构受外力作用而发生变形。在变形过程中,外力所做的功将转变为储存在弹性结构内的能量。当外力逐渐减小时,变形也逐渐减小,弹性结构又将释放出能量而做功。例如图13.5(a)所示的简支梁,在外力F1作用下发生弯曲变形而储存能量,当外力F1卸除后简支梁的变形将完全消失,然后又释放能量而恢复到原来的形状。弹性结构在外力作用下,因变形而储存的能量称为应变能。从另一角度来看,弹性结构在外力作用下将产生内力和变形,那么内力也将在其相应的变形上做功。结构的应变能可用内力所做的功来量度,即应变能等于内力所做的功。

与外力实功的定义类似,我们将内力在由其本身所引起的变形上所做的功称为内力实功。因为我们讨论的是静力平衡过程,所以结构的动能并没有变化。如果略去其他微小能量的损耗(如摩擦发生的热量),那么根据能量守恒定律,在加载过程中外力所做的实功将全部转化为结构的弹性应变能,也即外力所做的实功等于内力所做的实功。用U11表示图13.5(a)所示简支梁因外力F1作用所产生的内力在其相应变形上做的内力实功即应变能,于是有W11=U11。

若在F1作用的基础上,在梁上又施加另外一个静力荷载F2,梁就会达到新的平衡状态,如图13.5(b)所示。F1的作用点沿F1方向又将产生位移Δ12,F2的作用点沿F2方向产生了位移Δ22。由于Δ12不是由F1所引起的位移,所以F1沿Δ12所做的功便是外力虚功,用W12表示。显然,F2沿Δ22所做的功W22是实功。当然,F2所引起的内力也在将由它本身所引起的相应变形上做内力实功,用W22表示,同样有W22=U22。

将内力在由其他原因所引起的变形上所做的功称为内力虚功,那么,在F2的加载过程中,由F1所引起的内力在由F2所引起的相应变形上所做的功,是内力虚功,用U12表示。

在这里要强调,虚功之所以用“虚”字,只是强调做功的力与做功的位移无关,以示与实功的区别。同时还要注意,功和位移的表达符号都出现了两个脚标,第一个脚标表示位移发生的位置,第二个脚标表示引起位移的原因。因为实功是外力(或内力)在由其本身原因所引起的位移(或变形)上所做的功,其位移(变形)的方向始终与外力(内力)的方向相同,所以实功恒为正。而虚功则可能为正,可能为负,也可能等于零。