压杆稳定条件在建筑力学中的应用

下面只讨论折减系数法的稳定条件应用,将式(12.11)改写为:

式中　F——实际作用在压杆上的轴向压力;

A——截面的横截面面积;

φ——压杆的折减系数。

应用稳定条件,可对压杆进行三个方面的计算:

①稳定校核:即已知压杆的几何尺寸、所用材料、支承条件以及承受的压力,验算是否满足式(12.12)的稳定条件。

这类问题一般应首先计算出压杆的长细比λ,根据λ查出相应的折减系数φ,再按照式(12.12)进行校核。

②计算稳定时的许用荷载:即已知压杆的几何尺寸、所用材料及支承条件,按稳定条件计算其能够承受的许用荷载F值。

这类问题一般也要首先计算出压杆的长细比λ,根据λ查出相应的折减系数φ,再按照式[F]≤Aφ[σ]进行计算。

③进行截面设计:即已知压杆的长度、所用材料、支承条件以及承受的压力F,按照稳定条件计算压杆所需的截面尺寸。

这类问题一般采用“试算法”。这是因为在稳定条件(12.12)中,折减系数φ是根据压杆的长细比λ查表得到的,而在压杆的截面尺寸尚未确定之前,压杆的长细比λ不能确定,所以也就不能确定折减系数φ。因此,只能采用试算法。首先假定一折减系数φ值(0~1),由稳定条件计算所需要的截面面积A,然后计算出压杆的长细比λ,根据压杆的长细比λ查表得到折减系数φ,再按照式(12.12)验算是否满足稳定条件。如果不满足稳定条件,则应重新假定折减系数φ值,重复上述过程,直到满足稳定条件为止。

【例12.5】　如图12.8所示,构架由两根直径相同的圆杆构成,杆的材料为Q235钢,直径d=20mm,材料的许用应力[σ]=170MPa,已知h=0.4m,作用力F=15kN,试在计算平面内校核两杆的稳定性。

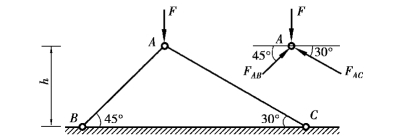
图12.8

【解】　①计算各杆承受的压力。取结点A为研究对象,根据平衡条件列方程有

解得

②计算两杆的长细比。

各杆的长度分别为

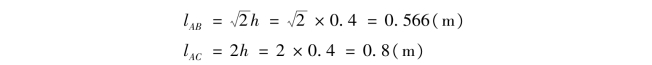
则两杆的长细比分别为

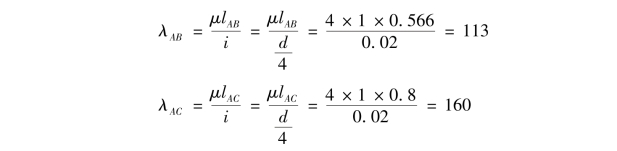
③查表得知折减系数

④按照稳定条件进行验算。

【例12.6】　如图12.9所示三铰支架,已知AB杆和BC杆都为圆形截面,直径d=50mm。材料为Q235钢,材料的许用应力[σ]=160MPa。在结点B处作用一竖向荷载F,AB杆的长为l=1.5m,按稳定条件考虑计算该三铰支架的许用荷载[F]。

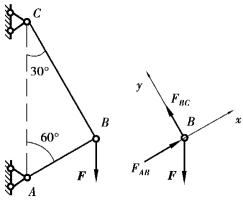
图12.9

【解】　①取点B为隔离体求各杆的内力。

(www.xing528.com)

则(压杆)。

则(拉杆)。

由此可知AB杆为压杆,受到的压力为F/2。

②计算长细比。

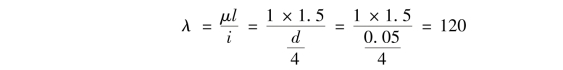
③查表得知折减系数φ=0.466。

④计算许用荷载[F]。将AB杆的压力F/2代入式[F]≤Aφ[σ]中,得

从压杆的稳定性考虑,其许用荷载[F]=292kN。

【例12.7】　如图12.10所示,一端固定一端铰支的压杆为工字钢,材料为Q235钢。已知杆长l=5m,F=300kN,材料的许用应力[σ]=160MPa,试选择工字钢的型号。

【解】　先假设φ=0.5,试选择截面尺寸、型号,算出λ后在查φ′。若φ′与假定的φ值相差较大,则再选二者的中间值重新计算,直至二者相差不大,最后再进行稳定校核。

①第一次试算,设φ1=0.5,则

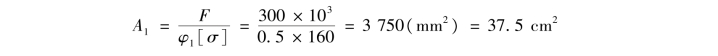
查型钢表,初选20b工字钢。该工字钢的截面面积A′1=39.5cm2,最小惯性半径&min=2.06cm,压杆柔度为

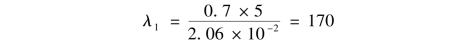
查表得折减系数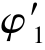=0.243,与φ1=0.5相差较大,故需进一步计算。

图12.10

②第二次试算,设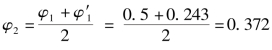,则

查型钢表,选25a工字钢,其横截面面积=48.5cm2,&min=2.4cm,压杆的柔度为

查表得折减系数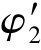=0.323,与φ2=0.372相差仍较大,故需再进一步计算。

③第三次试算,设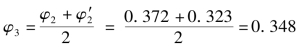,则

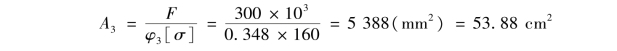
查型钢表,选28a工字钢,其截面面积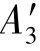=55.45cm2,&min=2.495cm,压杆的柔度为

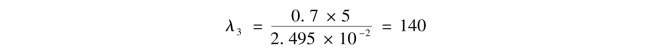
查表的折减系数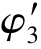=0.349,与φ3=0.348比较接近,故选用28a工字钢。

④稳定性校核。

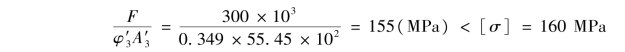
因此选用28a工字钢满足稳定性要求。

在稳定计算中,当遇到压杆局部截面被削弱的情况(例如有钻孔、开槽等)时,仍按没有被削弱的截面尺寸进行计算。这是因为压杆的临界力是由压杆整体的弯曲变形决定的,局部截面的削弱对整体弯曲变形的影响很小,也就是说对压杆临界力的影响很小,故可以忽略。但是,对这类压杆,除了进行稳定计算外,还应针对削弱了的横截面进行强度校核。