建筑力学（第2版）：压杆临界应力的计算方法与实例

综上所述,压杆的临界应力随着压杆柔度变化情况可用图12.5的曲线表示,该曲线是采用直线公式的临界应力总图,总图说明如下:

①当λ≥λp时,是细长杆,存在材料比例极限内的稳定性问题,临界应力用欧拉公式计算。

②当λs(或λb)≤λ<λp时,是中长杆,存在超过比例极限的稳定问题,临界应力用直线公式计算。

③当λ<λs(或λb)时,是短粗杆,不存在稳定性问题,只有强度问题,临界应力就是屈服强度σs或抗压强度σb。

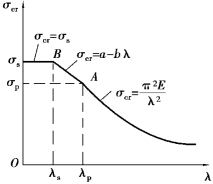
图12.5

由图12.5还可以看到,随着柔度的增大,压杆的破坏性质由强度破坏逐渐向失稳破坏转化。

【例12.3】　如图12.6所示为两端铰支的圆形截面受压杆,用Q235钢制成,材料的弹性模量E=200GPa,屈服强度σs=235MPa,直径d=40mm,试分别计算下面三种情况压杆的临界力:①杆长l=1.5m;②杆长l=0.8m;③杆长l=0.5m。

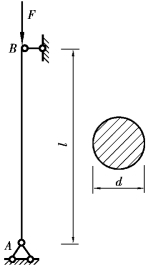
图12.6

【解】　①计算杆长l=1.5m时的临界力,两端铰支,因此μ=1。

惯性半径:。

柔度: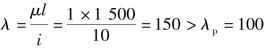,所以是大柔度杆,可以用欧拉公式计算。则

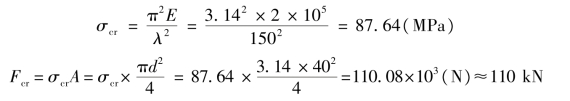
②计算杆长l=0.8m时的临界力

查表得λs=62,因为λs<λ<λp,所以该杆为中长杆,应用直线应验公式计算临界力,查表得a=304MPa,b=1.12MPa。

③计算杆长l=0.5m时的临界力

压杆为短粗杆,其临界力为(www.xing528.com)

【例12.4】　如图12.7所示的木柱,截面为120mm×200mm,l=7m,E=10GPa,λp=110。试求木柱的临界力和临界应力。

【解】　①计算最大刚度平面的临界力和临界应力,如图12.7(a)所示。

截面的惯性矩为:。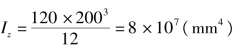

惯性半径为:。

两端铰接时长度系数为:μ=1。

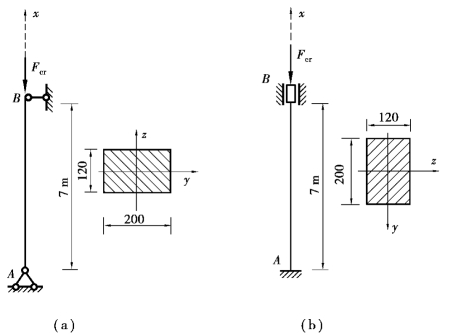
图12.7

其柔度为:。

因此可用欧拉公式计算,则

②计算最小刚度平面内的临界力和临界应力,如图12.7(b)所示。

截面的惯性矩为:。

惯性半径为:。

两端固定时长度系数为:μ=0.5。

柔度为:。

因此应用直线应验公式计算查表有a=28.7MPa,b=0.19MPa,则

σcr=a-bλ=28.7-0.19×101=9.51(MPa)

临界力

Fcr=σcrA=9.51×(120×200)=228.2×103(N)=228.2kN