建筑力学第2版-受压杆截面核心坐标及求解方法

工程中,有许多材料抗拉性能差,但抗压性能好且价格比较便宜,如砖、石、混凝土、铸铁等。在这类构件的设计计算中,往往认为其拉伸强度为零。这就要求构件在偏心压力作用下,其横截面上不出现拉应力。

由式(11.14)可知,中性轴在y,z轴上的截距与偏心力的偏心距成反比,由此说明,对于给定的截面,ey,ez值越小,ay,az值就越大,即外力作用点离形心越近,中性轴距形心就越远。因此,当外力作用点位于截面形心附近的一个区域内时,就可保证中性轴不与横截面相互,这个区域称为截面核心。当外力作用在截面核心的边界上时,与此相对应的中性轴就正好与截面的周边相切,如图11.16所示。利用这一关系就可确定截面核心的边界。

为确定任意形状截面(图11.16)的截面核心边界,可将与截面周边相切的任一直线①看作是中性轴,其在y,z两个形心主惯性轴上的截距分别为ay1和az1。由式(11.14)确定与该中性轴对应的外力作用点1,即截面核心边界上一个点的坐标(ey1,ez1):

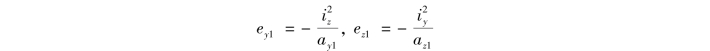
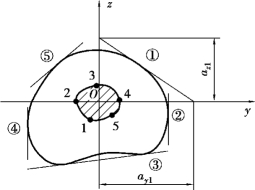
图11.16

同样,分别将与截面周边相切的直线②,③,…等看作是中性轴,并按上述方法求得与其对应的截面核心边界上点2,3,…的坐标。连接这些点所得到的一条封闭曲线,即为所求截面核心的边界,而该边界曲线所包围的带阴影线的面积,即为截面核心(图11.16),下面举例说明截面核心的具体作法。

【例11.8】　一矩形截面如图11.17所示,已知两边长度分别为b和h,求作截面核心。

【解】　先作与矩形四边重合的中性轴①,②,③和④,利用式(11.14)得

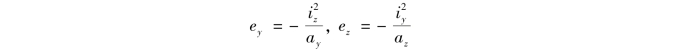
式中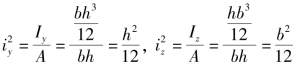,ay和az为中性轴的截距,ey和ez为相应的外力作用点的坐标。

对中性轴①,有,代入式(11.14),得

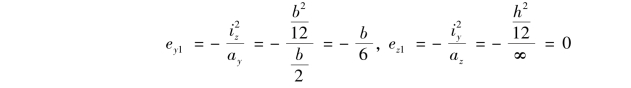
即相应的外力作用点为图11.17上的点1。

对中性轴②,有ay=∞,,代入式(11.14),得

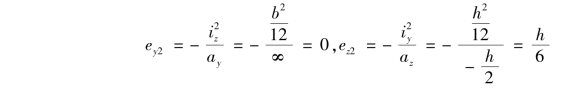(www.xing528.com)

即相应的外力作用点为图11.17上的点2。

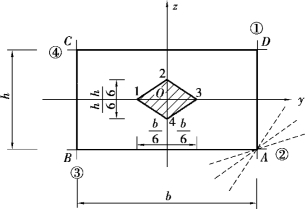
图11.17

同理,可得相应于中性轴③和④的外力作用点的位置如图上的点3和点4。

至于由点1到点2,外力作用点的移动规律如何,我们可以从中性轴①开始,绕截面点A作一系列中性轴(图中虚线),一直转到中性轴②,求出这些中性轴所对应的外力作用点的位置,就可得到外力作用点从点1到点2的移动轨迹。根据中性轴方程式(11.13),设ey和ez为常数,y0和z0为流动坐标,中性轴的轨迹是一条直线。反之,若设y0和z0为常数,ey和ez为流动坐标,则力作用点的轨迹也是一条直线。现在,过角点A的所有中性轴有一个公共点,其坐标为常数,相当于中性轴方程式(11.13)中的y0和z0,而需求的外力作用点的轨迹,则相当于流动坐标ey和ez。于是可知,截面上从点1到点2的轨迹是一条直线。同理可知,当中性轴由②绕角点B转到③,由③绕角点C转到④时,外力作用点由点2到点3、由点3到点4的轨迹都是直线。最后得到一个菱形(图中的阴影区),即矩形截面的截面核心为一菱形,其对角线的长度为截面边长的1/3。

对于具有棱角的截面,均可按上述方法确定截面核心。对于周边有凹进部分的截面(例如槽形或工字形截面等),在确定截面核心的边界时,应该注意不能取与凹进部分的周边相切的直线作为中性轴,因为这种直线显然与横截面相交。

【例11.9】　一圆形截面如图11.18所示,直径为d,试作截面核心。

【解】　由于圆截面对于圆心O是极对称的,因而,截面核心的边界对于圆心也是极对称的,即为一圆心为O的圆。在截面周边上任取一点A,过该点作切线①作为中性轴,该中性轴在y,z两轴上的截距分别为

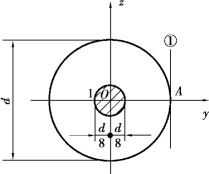
图11.18

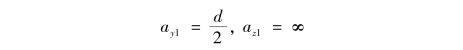
而圆形截面的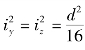,将以上各值代入式(11.14),即可得

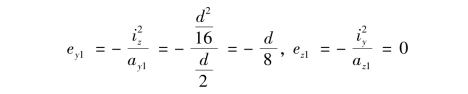
从而可知,截面核心边界是一个以O为圆心、以为半径的圆,即图中带阴影的区域。