(1)荷载简化
如图11.13(a)所示,已知F至z轴的偏心距为ey,至y轴的偏心距为ez。
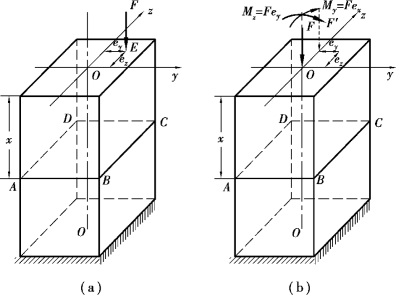
图11.13
首先将偏心压力F平移至z轴上(F′),附加力偶矩为Mz=Fey。再将压力F′从z轴上平移至与杆件轴线重合,附加力偶矩为My=Fez。如图11.13(b)所示,力F经过两次平移后,得到轴向压力F和两个力偶矩Mz,My,所以双向偏心压缩实际上就是轴向压缩和两个相互垂直的平面弯曲的组合。
(2)内力计算
由截面法截取任一横截面ABCD,其内力为
FN=-F,Mz=Fey,My=Fez
(3)应力计算
横截面ABCD上坐标为(y,z)的任意一点K的应力计算如下:
由轴力F引起K点的压应力为
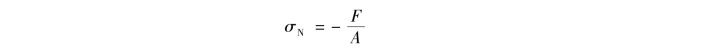
由弯矩Mz引起K点的应力为

由弯矩My引起K点的应力为
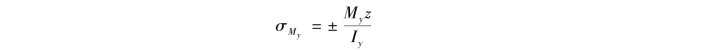
所以,K点的总应力为
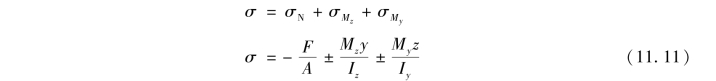
计算时,上式中F,Mz,My,y,z都可用绝对值代入,式中第二项和第三项前的正负号由观察弯曲变形的情况来确定。
(4)最大正应力
对于具有外棱角的横截面如矩形截面,处于双向偏心压缩时的最大应力和最小应力产生的位置可以直观判断。由图11.13(b)可见,横截面ABCD上的最大正应力(可能为拉、压或零)σmax发生在A点,而最小正应力(为最大压应力)σmin发生在C点,其值为

如果横截面没有外棱角,如图11.14所示的截面,y,z轴为形心主轴。对于这类截面,显然无法通过观察确定最大应力和最小应力发生的位置。但由于最大应力和最小应力必定发生在距中性轴最远的点处,因此可以先确定出中性轴的位置,然后确定出最大应力和最小应力发生的位置。下面来讨论如何确定中性轴位置。
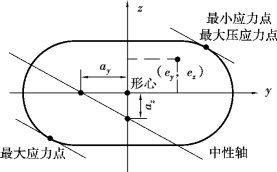
图11.14
根据式(11.11),横截面上得任意点的应力可表示为
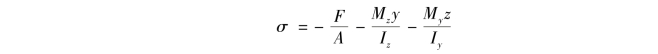
设y0,z0为中性轴上任一点的坐标,根据中性轴上各点的正应力等于零,则有(https://www.xing528.com)
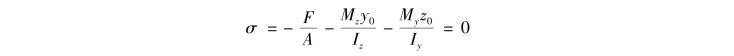
即
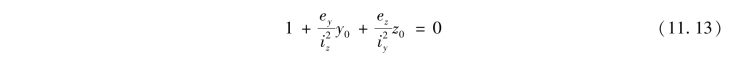
式中![]() 分别称为截面对z,y轴的惯性半径,也是截面的几何参数。式(11.13)称为中性轴方程,可见中性轴是一条不通过横截面形心的直线。
分别称为截面对z,y轴的惯性半径,也是截面的几何参数。式(11.13)称为中性轴方程,可见中性轴是一条不通过横截面形心的直线。
中性轴在y、z轴上的截距分别为
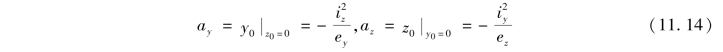
由此可以确定中性轴位置。由于中性轴截距ay,az和偏心距ey,ez符号相反,所以中性轴必与偏心力的作用点位于截面形心的相对两侧,如图11.14所示。如果中性轴把截面分为两部分,一部分为拉应力区,另一部分为压应力区。显然偏心压力作用点所在侧的区域为受压区,另一侧的区域为受拉区。
中性轴的位置确定后,作与中性轴平行并与截面周边相切的直线,受拉区切线的切点就是产生最大拉应力的位置,受压区切线的切点是产生最大压应力的位置,如图11.14所示。将两个切点的坐标分别代入式(11.11),即可求得最大的拉应力和最大的压应力。
当然,如果中性轴位于横截面之外,则全截面都为压应力区域,不会出现拉应力,其最大应力就是最小压应力。
(5)强度条件
根据上述的分析可知,双向偏心压缩(拉伸)杆件横截面上的所有点都只有正应力,处于单向应力状态,所以可类似于单向偏心压缩的情况建立相应的强度条件。
当杆件材料抗拉、抗压强度不相等且横截面同时出现拉压应力时,其强度条件为
![]()
对于如图11.13所示的矩形截面柱,其强度条件则为
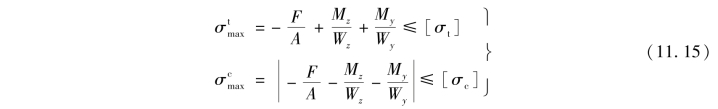
如果横截面不出现拉应力或材料抗拉、抗压强度相等,则只需按强度条件的第二个式子进行压应力强度计算即可。
【例11.7】 试求图11.15(a)所示偏心受压杆的最大拉应力和最大压应力。
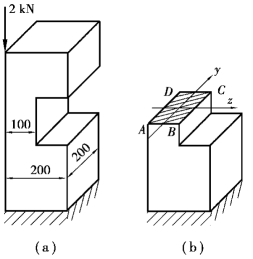
图11.15
【解】 此杆切槽处的截面〔图11.15(b)〕是危险截面。将力F向切槽截面的形心处简化,得
FN=-2kN
Mz=2×100×10-3=0.2(kN·m)
My=2×50×10-3=0.1(kN·m)
显然截面上C点产生最大的拉应力,而在截面A点产生最大的压应力,由式(11.12)可得
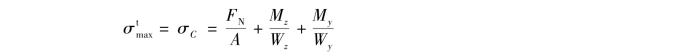
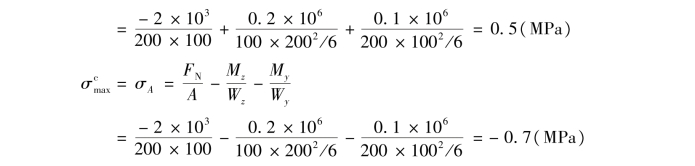
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




