斜弯曲梁应力与强度计算：建筑力学

矩形截面悬臂梁的自由端处作用一个垂直于梁轴线并通过截面形心的集中荷载F,F与横截面对称轴y成φ角,如图11.2(a)所示。由于外力不在纵向对称平面内,梁在弯曲过程中,轴线不能始终保持在力与轴线所确定的平面内,而是不断向平面外倾斜翘出。故称为斜弯曲。现以该梁为例,分析斜弯曲时的应力和强度计算问题。

图11.2

(1)荷载分解

将荷载F沿截面的两个对称轴y、z分解为两个分量:

Fy=Fcosφ,Fz=Fsinφ

由图11.2(a)可知,Fy将使梁在Oxy纵向对称面内发生平面弯曲,z轴为中性轴;Fz将使梁在Oxz纵向对称面内发生平面弯曲,y轴为中性轴。由此可见,斜弯曲可以分解为两个相互垂直的平面弯曲的组合。图11.1(a)中的檩条也产生这种斜弯曲变形。

(2)内力分析

与平面弯曲问题一样,梁的横截面上虽然存在着剪力和弯矩两种内力,但由剪力所产生的切应力影响很小,其强度是由弯矩所引起的正应力来控制的。所以,在此忽略剪力,只计算弯矩。

如图11.2(b)所示,Fy和Fz在距固定端为x处任意横截面上引起的弯矩分别为:

Mz=Fy(l-x)=F(l-x)cosφ=Mcosφ

My=Fz(l-x)=F(l-x)sinφ=Msinφ

式中,M=F(l-x)为力F引起的截面上的总弯矩。弯矩Mz、My分别作用在梁的纵向对称面Oxy,Oxz内。

(3)应力分析

利用弯曲正应力公式,可求得由Mz和My引起的K(y,z)点处的正应力分别为:

由叠加原理,任意点K的总正应力为:

代入总弯矩M=F(l-x),可得

式中Iz和Iy为横截面对形心主轴z和y的惯性矩;y和z为K点坐标。具体计算时,M、y、z均以绝对值代入,而σK的正负号,可通过K点所在位置直观判断,如图11.2所示。

(4)最大正应力

梁在斜弯曲情况下的强度仍由最大正应力来控制。因此,为了进行强度计算,必须求出梁内的最大正应力。横截面上的最大正应力发生在离中性轴最远处,故要求得最大正应力,必须先确定中性轴的位置。由于在中性轴上各点的正应力都等于零,为此令点P(y0,z0)代表中性轴上的任一点,将它的坐标值代入式(11.1b),即可得中性轴方程:

由式(11.2)可知,中性轴是一条通过截面形心的直线。设中性轴n—n与z轴间的夹角为α〔图11.2(c)〕,则

在一般情况下,Iy≠Iz,故α≠φ,即中性轴不垂直于荷载作用平面。只有当φ=0°,φ=90°或Iy=Iz时,才有α=φ,中性轴才垂直于荷载作用平面。显而易见,φ=0°或φ=90°的情况就是平面弯曲情况,相应的中性轴就是z轴或y轴。对于正方形、圆形等截面以及某些特殊组合截面,其Iy=Iz,故α=φ,因而,正应力可用合成弯矩M进行计算。

梁横截面上的最大正应力发生在截面上离中性轴最远的点处,例如图11.2(c)中的A、C两点处,且点A处的正应力为最大拉应力,点C处的正应力为最大压应力。将A、C两点的坐标(yA,zA),(yC,zC)代入式(11.1b),并因,可以得到:

式(11.4)对于具有凸角而又有两条对称轴的截面(如矩形、工字形截面等)均适用。(www.xing528.com)

(5)强度计算

梁内的最大正应力发生在最大弯矩为Mmax的截面(危险截面)上,如果Mmax的两个分量为Mzmax和Mymax,代入式(11.4)即可得整个梁的最大正应力σmax。当梁的材料抗拉压能力相同,则斜弯曲梁的强度条件为

当材料的抗拉、压强度不同,则须分别对拉、压强度进行计算。

【例11.1】　如图11.3(a)所示为一房屋的桁架结构。已知:屋面坡度为122,两榀桁架之间的距离为4m,木檩条的间距为1.5m,屋面重(包括檩条)为1.6kN/m2。若木檩条采用120mm×180mm的矩形截面,所用松木的许用应力为[σ]=10MPa。试校核木檩条的强度。

【解】　①确定计算简图。屋面的重量是通过檩条传给桁架的。檩条简支在桁架上,其计算跨度等于二桁架间的距离l=4m,檩条上承受的均布荷载q=1.6×1.5=2.4kN/m,其计算简图如图11.3(b)和(c)所示。

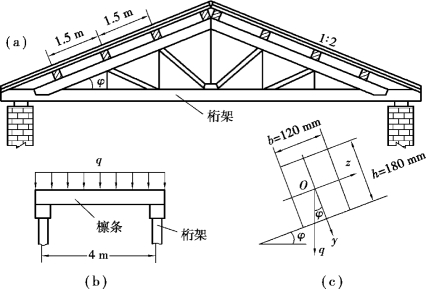
图11.3

②内力及有关数据的计算。

屋面坡度为122,即tan或φ=26°34′,故

sinφ=0.4472,cosφ=0.8944

另外算出

③强度校核。

由强度条件式(11.5),可得

σmax>[σ]=10MPa,而且超过的数值大于[σ]的5%,故不能满足强度要求。

【例11.2】　一长2m的矩形截面木制悬臂梁,弹性模量E=1.0×104MPa,梁上作用有两个集中荷载F1=1.3kN和F2=2.5kN,如图11.4(a)所示,设截面b=0.6h,[σ]=10MPa。试选择梁的截面尺寸。

图11.4

【解】　将自由端的作用荷载F1分解

F1y=F1sin15°=0.336kN

F1z=F1cos15°=1.256kN

此梁的斜弯曲可分解为在xOy平面内及xOz平面内的两个平面弯曲,如图11.4(c)所示。由图11.4可知Mz和My在固定端的截面上达到最大值,故危险截面上的弯矩

上式中Mz与My只取绝对值,且截面上的最大拉压应力相等,故

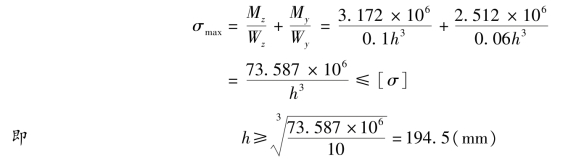
可取h=200mm,b=120mm。