梁正应力强度计算方法建筑力学

利用强度条件可进行强度校核、截面设计和确定许可荷载三类强度计算问题。

(1)强度校核

已知梁的横截面形状和尺寸、材料及作用在梁上的荷载,判断式(10.11)是否成立,以校核梁是否具有足够的正应力强度。

(2)设计截面尺寸

已知作用在梁上的荷载和制造梁的材料,根据强度条件,先计算出所需的最小抗弯截面系数

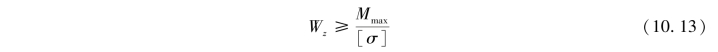
然后根据梁的截面形状,由Wz值确定截面的具体尺寸或型钢型号。

(3)确定许用荷载

已知梁的材料、横截面形状和尺寸,根据强度条件计算出梁所能承受的最大弯矩

然后根据Mmax与荷载的关系,计算出梁所能承受的最大荷载。

【例10.3】　一矩形截面悬臂梁在自由端受集中力作用,截面尺寸如图10.12(a)所示。已知材料的许用应力[σ]=160MPa。试校核梁的正应力强度。

【解】　①绘制弯矩图,如图10.12(b)所示。由M图可知最大弯矩发生在固定端截面A上,截面A为危险截面,最大弯矩值Mmax=72kN·m。

②计算抗弯截面系数:

图10.12

③校核正应力强度:

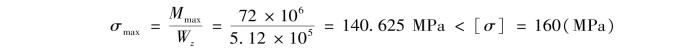
所以,该悬臂梁满足正应力强度条件,具有足够的强度。

【例10.4】　如图10.13(a)所示的T形截面外伸梁,已知材料的许用拉应力[σt]=32MPa,许用压应力[σc]=70MPa。试按正应力强度条件校核梁的强度。

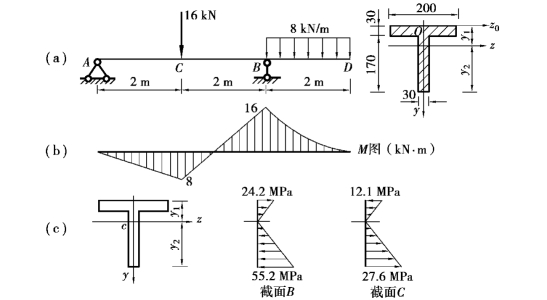
图10.13

【解】　①绘制梁的弯矩图,如图10.13(b)所示。由M图可知,截面B上最大负弯矩MB=16kN·m,截面C上有最大正弯矩MC=8kN·m。

②计算截面的几何特征值。首先确定截面的形心位置,以yOz0为参考坐标系,由形心的坐标公式可得

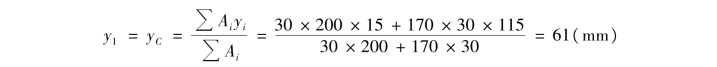
由T形截面的几何尺寸可知

y2=200-y1=200-61=139(mm)

计算截面对中性轴的惯性矩

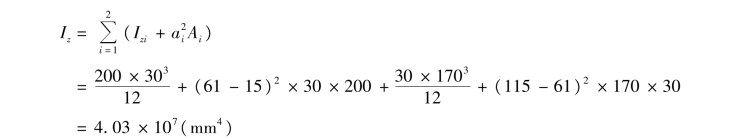
计算抗弯截面系数

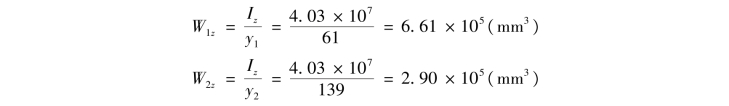
③校核强度。图中所示梁的许用拉压应力不相等,截面又不对称于中性轴,因此,对该梁的最大正弯矩和最大负弯矩所在截面均应进行强度校核。

校核截面B的强度:截面B上有最大的负弯矩,最大拉应力发生在截面上边缘各点,最大压应力发生在截面下边缘各点,其值为

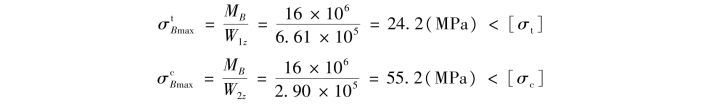
校核截面C的强度:截面C上有最大的正弯矩,最大拉应力发生在截面下边缘各点,最大压应力发生在截面上边缘各点,其值为

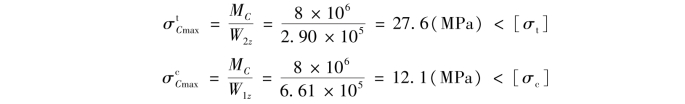
正应力分布情况如图10.13(c)所示。

计算结果表明,最大拉压应力均没有超过相应的许用应力,因此该梁的强度足够。

在本例中,最大拉应力发生在截面C的下边缘各点,而最大压应力发生在截面B的上边缘各点。梁的材料拉压极限应力不同,因此该梁有两个危险截面,即截面B是压应力的危险截面,截面C是拉应力的危险截面。

【例10.5】　如图10.14(a)所示悬臂梁,采用热轧工字钢制成。已知材料的许用应力[σ]=160MPa。试选择工字钢的型号。

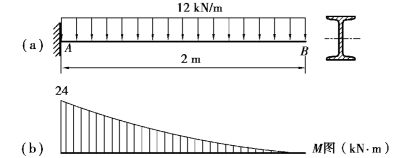
图10.14

【解】　①绘制弯矩图,如图10.14(b)所示。由M图可知,最大弯矩值Mmax=24kN·m。

②计算工字钢所需要的抗弯截面系数。由强度条件可得

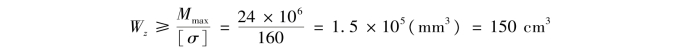
③选择工字钢型号。查型钢表,16号工字钢的抗弯截面系数Wz=185cm3,比所需的Wz略大,因此该梁采用16号工字钢。

【例10.6】　某简支梁的计算简图如图10.15(a)所示。材料的许用应力[σ]=170MPa。若该梁分别采用热轧工字钢、矩形(设b/h=2/3)和圆形截面制成。试分别设计三种截面的尺寸,并比较三种截面梁的合理性。

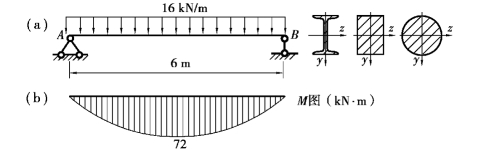
图10.15

【解】　①绘制梁的弯矩图,如图10.15(b)所示,最大弯矩值。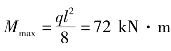

②计算梁所需要的抗弯截面系数Wz。(www.xing528.com)

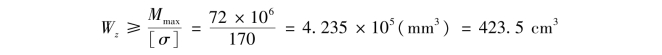
③分别计算三种横截面的截面尺寸。

a.热轧工字钢的型号。由型钢表,查得25b号工字钢的Wz=422.7cm3,虽小于所需的抗弯截面系数,但相差甚微,显然没有超过5%,能满足强度要求,故可采用选用25b号工字钢。

b.计算矩形截面的尺寸。由矩形截面的抗弯截面系数

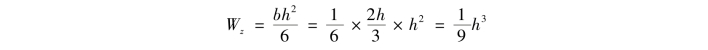
得

取截面的高度h=156mm,则截面的宽度为

c.计算圆形截面的尺寸。由圆形截面的抗弯截面系数,得

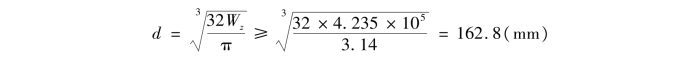
取圆截面的直径d=163mm。

④比较三种截面梁的合理性。所谓合理性的比较,就是在梁的跨度和所受荷载相同的情况下,哪种截面所用的材料越少就越合理。由于是同种材料,所以材料用量之比就是体积之比,而梁的跨度相同,体积之比就等于截面面积之比。为此,先计算三种截面的面积。

a.工字形截面:查得25b号工字钢截面的面积A工=53.5cm2=5350mm2。

b.矩形截面的面积:A矩=bh=156×104=16224(mm2)。

c.圆形截面的面积:。

三种截面梁的材料用量之比为

A工2A矩2A圆=5350216224220856=123.0323.90

即矩形截面梁所用材料是工字形截面梁的3.03倍,而圆形截面梁所用材料是工字形截面梁的3.90倍。显然,这三种形式的截面梁中,工字形截面梁最合理,圆形截面梁最不合理。

【例10.7】　如图10.16(a)所示外伸梁,采用箱形截面,尺寸如图所示。材料的许用应力[σ]=160MPa。试确定梁的许用荷载[F]。

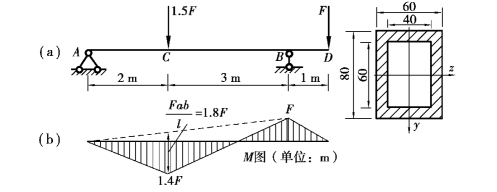
图10.16

【解】　①绘制梁的弯矩图,如图10.16(b)所示。由M图可知,最大弯矩发生在截面C上,即

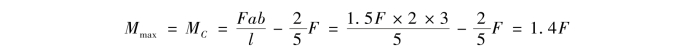
②计算抗弯截面系数:

截面对中性轴的惯性矩为

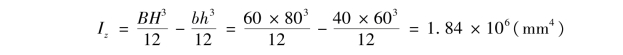
抗弯截面系数为

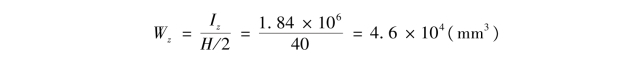
③计算该梁所能承受的最大弯矩。

由强度条件得

④确定许可荷载。由①可得

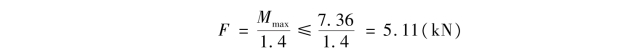
取

[F]=5kN

【例10.8】　如图10.17所示木质简支梁,材料的许用应力[σ]=10MPa,截面为矩形,尺寸如图所示。试确定:

①当截面按如图10.17(a)所示方式竖放时,梁的许可荷载[q1];

②当截面按如图10.17(b)所示方式横放时,梁的许可荷载[q2]。

【解】　①绘制梁的弯矩图,如图10.17(c)所示。由M图可知,跨中截面的弯矩最大。

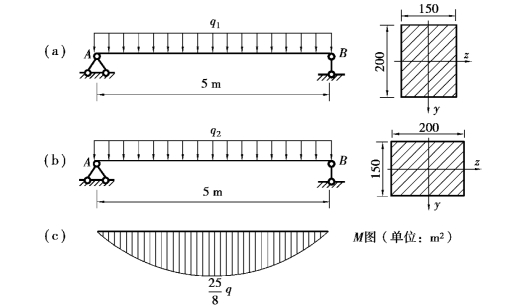
图10.17

②确定截面按如图10.17(a)所示方式竖放时的许可荷载。由强度条件可得

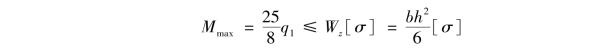
于是有

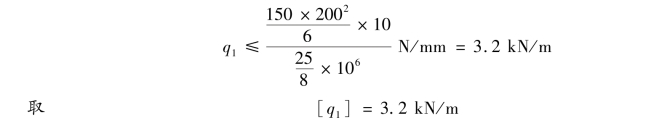
③确定截面按如图10.17(b)所示方式竖放时的许可荷载。由强度条件可得

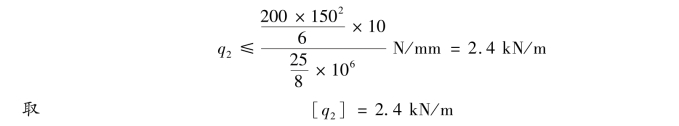
通过以上的计算可以发现,相同的矩形截面梁,截面竖向时的承载能力比横竖时提高了25%。因此,矩形截面梁应竖放(即高度大于宽度),而不适宜横放。