为了使所研究的问题简单,以矩形截面梁为例,先讨论梁纯弯曲时横截面上的正应力计算,然后再推广到梁的一般情况。研究梁纯弯曲时横截面上的正应力计算,要综合考虑变形的几何关系、物理关系和静力学关系三个方面。
(1)变形的几何关系
梁纯弯曲时,横截面上的正应力是如何分布的?怎样计算正应力的大小?要回答这些问题,就应先研究该截面上任一点处的变形,而梁内部的变形是无法直接观察到的,可以通过观察表面变形的现象来推测内部的变形。为此,取一段矩形截面等直梁,受力之前在其表面画上一系列代表纵向纤维的纵向线和一系列代表横截面边缘的横向线。纵向线与轴线平行,横向线与轴线垂直,这样纵向线与横向线就在梁的表面形成了一系列矩形小方格,如图10.2(a)所示。当在梁的两端施加一对大小相等、转向相反、作用面与横截面垂直的力偶,梁将产生纯弯曲变形,这时可以明显地观察到如图10.2(b)所示的变形现象:
①所有纵向线均变成了曲线,并仍然与变形后的梁轴线(挠曲线)平行;而且靠近梁凸边(下边缘)的纵向线伸长了,而靠近梁凹边(上边缘)的纵向线缩短了。
②所有的横向线仍为直线,只不过相互倾斜了一个角度,但仍然与变形后的纵向线垂直,即原来各矩形方格的直角在梁变形后仍然为直角。
③横截面的高度没有发生变化,但矩形截面梁的凸边(下部)宽度变窄,而凹边(上部)宽度变宽,如图10.2(c)所示。
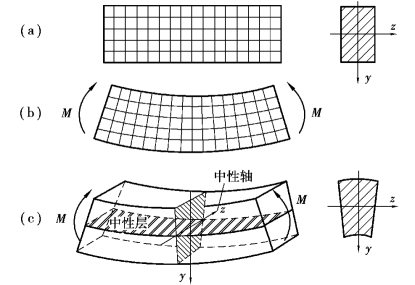
图10.2
根据上面观察到的表面变形现象,通过判断和推理,可对纯弯曲梁作如下假设:
①平面假设。变形前为平面的横截面,变形后仍为平面,它像刚性平面一样绕某轴旋转了一个角度,但仍垂直于梁变形后的轴线。
②单向受力假设。可将梁视为由无数根纵向纤维所组成,由于横截面的高度没有发生变化,因此可认为,各纵向纤维之间无挤压变形现象;同时,由于纵向线与横向线之间的直角在变形前后没有改变,便没有剪切变形,因此各纵向纤维只发生了单向拉伸或压缩变形。
③各纵向纤维的变形大小与其所在横截面宽度方向的位置无关,只与其在高度方向位置有关,即在梁横截面上位于同一高度的纵向纤维变形均相同。
根据现象③和单向受力假设,梁下部的纵向线伸长,截面变窄,表示梁下部各纤维受到伸长变形;梁上部的纵向线缩短,截面变宽,表示梁上部各纤维受到压缩变形。从下部各层纤维伸长到上部各层纤维缩短的连续变形中,必有一层纤维既不伸长也不缩短,这层纤维称为中性层,中性层与横截面的互线称为中性轴,如图10.2(c)所示。中性轴将截面分为两个区:凸边一侧为受拉区,凹边一侧为受压区。根据平面假设可知,纵向纤维伸长或缩短是由于横截面绕中性轴转动的结果。由于平面弯曲梁的外力作用在梁的纵向对称平面内,故梁的变形也对称于此平面。因此,中性轴应垂直于截面的对称轴y,如图10.2(c)所示。
根据上述假设和推理,通过几何关系便可求出横截面上任一点处纵向纤维的线应变,从而找出纵向线应变的变化规律。为此,用相邻的两截面m—m,n—n从梁上截取一微段梁dx进行分析〔图10.3(a)〕,O1O2为中性层。以中性轴为z轴,以截面的纵向对称轴为y轴,向下为正。现讨论距中性层y处的纵向纤维 的线应变〔图10.3(b)〕。
的线应变〔图10.3(b)〕。
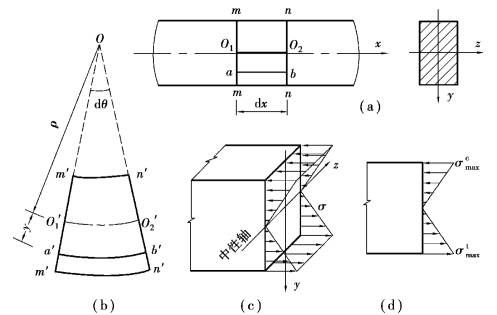
图10.3
如图10.3(b)所示,梁变形后截面m—m,n—n间相对转角为dθ,纤维![]() 由直线变成弧线
由直线变成弧线![]() ,O为中性层的曲率中心,曲率半径用ρ表示。纤维
,O为中性层的曲率中心,曲率半径用ρ表示。纤维![]() 的原长
的原长![]() ,因此,纤维
,因此,纤维![]() 的纵向变形为
的纵向变形为
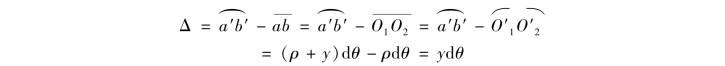
其线应变为
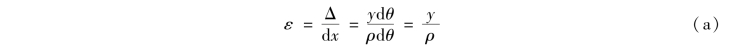
该式表明,横截面上各点处的纵向线应变ε与该点到中性轴的距离y成正比。
(2)物理关系
因为纵向纤维之间无挤压,每根纵向纤维均是单向拉伸或压缩,分别与轴向拉压杆的纵向纤维类似。由此可知纯弯曲梁横截面上各点只有正应力。当正应力不超过材料的比例极限σp时,由胡克定律可知
![]()
将(a)式代入(b)式得
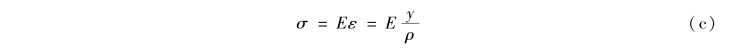
(c)式表明,横截面上任意点的正应力与该点到中性轴的距离成正比。综合前面的分析,可以得出梁纯弯曲时横截面上正应力的分布规律:正应力沿横截面的高度呈线性变化,并以中性轴为界,一侧为拉应力,另一侧为压应力;中性轴上各点处的正应力为零,到中性轴等距离各点处的正应力相等;距中性轴最远点处将产生最大拉应力或最大压应力,如图10.3(c)、(d)所示。
(3)静力学关系
如图10.4所示,在梁的横截面上取微面积dA,其上的法向微内力为σdA,此微内力沿梁轴线方向的合力为![]() ,它应等于该横截面上的轴力FN。而梁纯弯曲时,横截面上并没有轴力,即FN=0,于是有
,它应等于该横截面上的轴力FN。而梁纯弯曲时,横截面上并没有轴力,即FN=0,于是有

图10.4
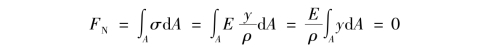
式中,![]() 常量,且不等于零,则有(https://www.xing528.com)
常量,且不等于零,则有(https://www.xing528.com)
![]()
Sz是横截面对中性轴z的面积矩,Sz=0说明横截面的中性轴z必定通过截面的形心。
同时,横截面上的所有微内力σdA对z轴的合力偶矩为![]() ,并等于该横截面上的弯矩M,于是有
,并等于该横截面上的弯矩M,于是有

式中积分
![]()
是横截面对z轴(中性轴)的惯性矩。因此可得
![]()
即

式中,![]() 是梁变形后轴线的曲率。该式表明,EIz越大,曲率
是梁变形后轴线的曲率。该式表明,EIz越大,曲率![]() 就越小,那么梁的变形也就越小,说明梁抵抗弯曲变形的能力就越强,故EIz称为梁的抗弯刚度。将式(10.1)代入式(c)可得纯弯曲梁横截面上任意点正应力计算公式:
就越小,那么梁的变形也就越小,说明梁抵抗弯曲变形的能力就越强,故EIz称为梁的抗弯刚度。将式(10.1)代入式(c)可得纯弯曲梁横截面上任意点正应力计算公式:
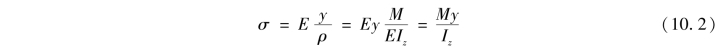
式中,M为横截面上的弯矩;y为所求正应力点到中性轴的距离;Iz为横截面对中性轴z的惯性矩,只与横截面的形状、尺寸有关,常用单位为m4或mm4,是横截面的几何特征之一(详见附录Ⅰ)。
应用公式(10.2)计算正应力时,通常不考虑式中M和y的正负号,而以其绝对值代入,正应力σ的正负号可根据梁的变形情况直接判断。以中性轴为界,梁凸出的一侧为拉应力,凹进的一侧为压应力。
由正应力计算公式的推导过程可知,它们的适用条件是:处于线弹性范围内(σmax≤σp)的纯弯曲梁。式(10.2)虽然是由矩形截面梁推导出来的,但在推导过程中并没有用到矩形的几何性质。因此,只要梁有一纵向对称面,且荷载作用在该平面内,如图10.5所示的圆形、圆环形、工字形、T形等截面梁,公式均适用。

图10.5
【例10.1】 矩形截面简支梁的截面尺寸如图10.6所示,在对称位置承受两集中力作用。试求梁跨中截面a,b,c三点处的正应力。

图10.6
【解】 ①绘制梁的内力图,如图10.6(b)、(c)所示。由内力图知,梁的跨中截面位于梁的CD段,该段剪力FQ=0,弯矩M=30kN·m,是纯弯曲梁段。
②计算正应力。根据图中所示尺寸,计算矩形截面的惯性矩

由式(10.2)计算跨中截面各点的正应力:
a点处的正应力

b点处的正应力

c点处的正应力
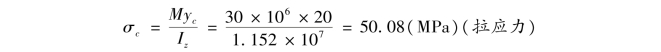
三点处正应力的正负也可由变形直接判定,a,c两点在受拉一侧,其应力为拉应力,而b点在受压一侧,则其应力为压应力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




