静定平面桁架内力计算方法

静定平面桁架的内力计算的方法通常有结点法和截面法。

(1)结点法

结点法是截取桁架的一个结点为隔离体,利用该结点的静力平衡方程来计算截断杆的轴力。由于作用于桁架任一结点上的各力(包括荷载、支座反力和杆件的轴力)构成了一个平面汇互力系,而该力系只能列出两个独立的平衡方程,因此所取结点的未知力数目不能超过两个。结点法适用于简单桁架的内力计算。一般先从未知力不超过两个的结点开始,依次计算,就可以求出桁架中各杆的轴力。

①零杆的判定。桁架中有时会出现轴力为零的杆件,称为零杆。在计算内力之前,如果能把零杆找出,将会使计算得到简化。通常在下列几种情况中会出现零杆:

a.不共线的两杆组成的结点上无荷载作用时,该两杆均为零杆,如图9.10(a)所示。

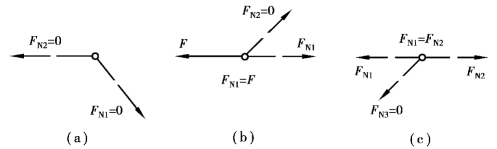
图9.10

b.不共线的两杆组成的结点上有荷载作用时,若荷载与其中一杆共线,则另一杆必为零杆,如图9.10(b)所示。

c.三杆组成的结点上无荷载作用时,若其中有两杆共线,则另一杆必为零杆,且共线的两杆内力相等,如图9.10(c)所示。

②比例关系的应用。在列平衡方程时,经常要将桁架中斜杆的轴力FN分解成水平分力FNx和竖向分力FNy(图9.11)。FN,FNx,FNy构成一个三角形,杆件AB的长度l及其在水平方向的投影长度lx和竖直方向的投影长度ly也构成了一个三角形,由于两个三角形相似,因而存在如下的比例关系:

图9.11

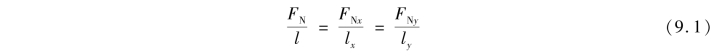
应用上述比例关系,可以避免计算斜杆的倾角θ及其三角函数,以减少工作量。

在桁架的内力计算中,一般先假定各杆的轴力为拉力,若计算的结果为负值,则该杆的轴力为压力。此外,为避免求解联立方程,应恰当地选取投影轴,尽可能使一个平衡方程中只包含一个未知力。

【例9.4】　求如图9.12(a)所示桁架各杆的轴力。

【解】　①求支座反力。由整体的平衡方程,可得支座反力为

FAx=0,FAy=40kN,FB=40kN

②求各杆的内力。在计算之前先找出零杆。由对结点C,G的分析,可知杆CD,GH为零杆。

此桁架和荷载都是对称的,只要计算其中一半杆件的内力即可,现计算左半部分。从只包含两个未知力的结点A开始,顺序取结点C,D,E为隔离体进行计算。

取结点A为隔离体〔图9.12(b)〕,由∑Fy=0得

FNADy=10kN-40kN=-30kN

利用比例关系,得

由∑Fx=0得

FNAC=-FNADx=60kN

取结点C为隔离体〔图9.12(c)〕,由∑Fx=0得

FNCF=FNAC=60kN

取结点D为隔离体〔图9.12(d)〕,列出平衡方程

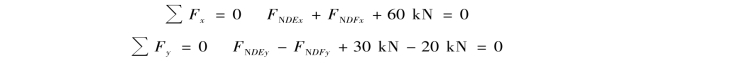
利用比例关系,得

FNDEx=2FNDEy

FNDFx=2FNDFy

代入平衡方程,得

2FNDEy+2FNDFy+60kN=0

FNDEy-FNDFy+10kN=0

解得

FNDEx=-40kN,FNDEy=-20kN,FNDE=-44.7kN

FNDFx=-20kN,FNDFy=-10kN,FNDF=-44.7kN

取结点E为隔离体〔图9.12(e)〕,由结构的对称性,FNEHy=FNDEy=-20kN。(www.xing528.com)

由∑Fy=0得

FNEF=2×20kN-20kN=20kN

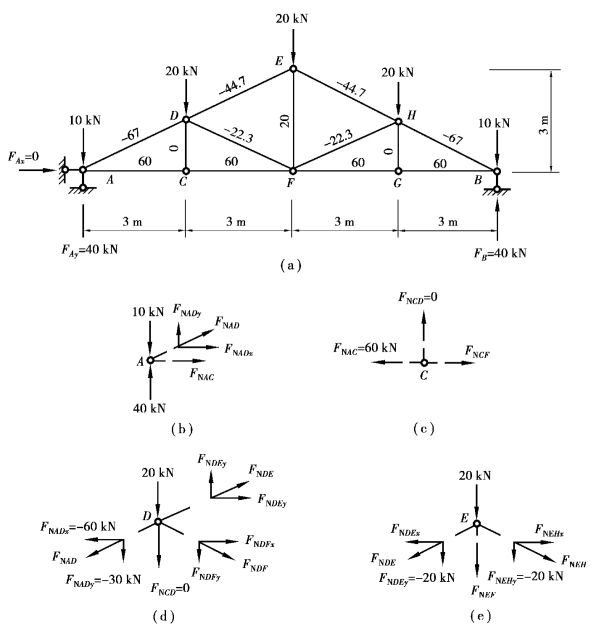
图9.12

内力计算完成后,将各杆的轴力标在图上〔图9.12(a)〕,图中轴力的单位为kN。

(2)截面法

截面法是用一截面(平面或曲面)截取桁架的某一部分(两个结点以上)为隔离体,利用该部分的静力平衡方程来计算截断杆的轴力。由于隔离体所受的力通常构成平面一般力系,而一个平面一般力系只能列出3个独立的平衡方程,因此用截面法截断的杆件数目一般不应超过3根。截面法适用于求桁架中某些指定杆件的轴力。用截面法计算杆的轴力时,为避免求解联立方程,应恰当地选取投影轴和矩心,尽可能使一个平衡方程中只包含一个未知力。

对于联合桁架必须先用截面法求出联系杆的轴力,然后与简单桁架一样用结点法求各杆的轴力。一般地,在桁架的内力计算中,往往是结点法和截面法联合加以应用。

【例9.5】　求如图9.13(a)所示的桁架中杆a,b,c,d的轴力。

【解】　①求支座反力。由整体平衡方程,可得支座反力为

FAx=0,FAy=50kN,FB=30kN

②求杆a,b,c的内力。

图9.13

用截面Ⅰ—Ⅰ截取桁架的左半部分为隔离体〔图9.13(b)〕,列平衡方程:

由∑MD=0,FNc×4m-20kN×3m-50kN×3m=0

得

FNc=52.5kN

由∑MF=0,-FNa×4m+20kN×3m+20kN×6m-50kN×9m=0

得

FNa=-67.5kN

由

∑Fx=0,FNa+FNbx+FNc=0

得

FNbx=-FNa-FNc=15kN

利用比例关系,得

③求杆d的内力。联合应用结点法和截面法计算杆d的内力较为方便。先取结点E为隔离体〔图9.13(c)〕,由平衡方程∑Fx=0,得

FNCE=FNc=52.5kN

再用截面Ⅱ—Ⅱ截取桁架左半部分为隔离体〔图9.13(d)〕,列平衡方程

∑MD=0,FNdx×4m+52.5kN×4m-50kN×3m=0

得

FNdx=-15kN

利用比例关系,得

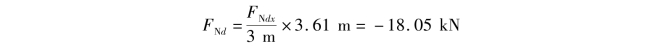
如前所述,用截面法计算桁架内力所截断的杆件一般不应超过3根。当被截断的杆件超过3根时,其中某根杆件的轴力也可选取适当的平衡方程求出。例如对图9.14(a)所示桁架,欲求杆ED的轴力,可用Ⅰ—Ⅰ截面将桁架截开,在被截断的5根杆件中,除杆ED外,其余4杆均会交于结点C,由力矩方程∑MC=0即可求得FNED。

图9.14

又如图9.14(b)所示的复杂桁架,欲求杆CB的轴力,可用Ⅰ—Ⅰ截面将桁架截开,在被截断的4根杆件中,除杆CB外,其余3根杆互相平行,选取y轴与此3根杆垂直,由投影方程∑Fy=0即可求得FNCB。