叠加法绘制弯矩图|建筑力学第2版

建筑力学讨论的内容是基于构件发生小变形的假设,在此假设前提下,当材料服从胡克定律时,构件的支座反力、内力、应力和变形等力学量均与外力间为线性关系。当构件上有几个荷载共同作用时,由每一个荷载引起的构件的支座反力、内力、应力和变形等力学量都不受其他荷载作用的影响,这种特性称为力的独立作用原理。这时,构件上的支座反力、内力、应力和变形等力学量可由各个荷载分别单独作用时的这些力学量叠加得到,称为叠加原理。

基于以上讨论,梁在几个荷载共同作用下所产生的内力,等于每个荷载单独作用时所产生的内力之和。叠加原理反映了荷载对构件影响的各自独立性。下面用例题说明如何用叠加原理来作梁的内力图。

【例8.13】　试用叠加法作如图8.26(a)所示简支梁的剪力图和弯矩图。

【解】　①荷载分组。首先将如图8.26(a)所示简支梁上作用的荷载看成两个分别由F和q单独作用下的简支梁〔图8.26(b)、(c)〕。

②内力计算。分别作出简支梁单独在集中力F和单独在均布荷载q作用下的剪力图和弯矩图,如图8.26(e)、(f)、(h)、(i)所示。图8.26(e)、(h)是该简支梁在集中力F单独作用时的剪力图、弯矩图;图8.26(f)、(i)是该梁在均布荷载q单独作用时的剪力图和弯矩图。

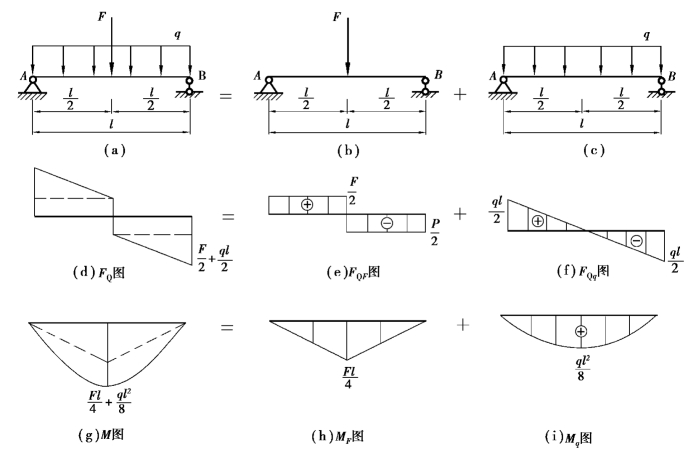
图8.26

③叠加内力图。根据叠加原理,在集中力F和均布荷载q共同作用下,其每个截面上的剪力、弯矩是集中力F和均布荷载q分别作用时该载面上的剪力、弯矩(图中的竖标)相叠加。因此,简支梁在q,F共同作用下的剪力、弯矩图,如图8.26(d)、(g)所示,应该等于该简支梁单独在集中力F和均布荷载q作用下的代数和。应该注意,两个弯矩、剪力图的叠加并非是两图形的简单拼合,而是指两图中对应的纵坐标相叠加。这样,同侧的纵坐标应相加,异侧的纵坐标应相减。

【例8.14】　试用叠加法作图8.27所示悬臂梁的剪力、弯矩图。

【解】　①荷载分组。首先将如图8.27(a)所示悬臂梁上作用的荷载看成两个分别由F和q单独作用下的悬臂梁,如图8.27(b)、(c)所示。(www.xing528.com)

②内力计算。分别作出悬臂梁单独在集中力F和单独在均布荷载q作用下的剪力图和弯矩图,如图8.27(e)、(f)、(h)、(i)所示。如图8.27(e)、(h)是该悬臂梁在集中力F单独作用时的剪力图、弯矩图;图8.27(f)、(i)是该梁在均布荷载q单独作用时的剪力图和弯矩图。

③叠加内力图。根据叠加原理,在集中力F和均布荷载q共同作用下,其每个截面上的剪力、弯矩是集中力F和均布荷载q分别单独作用时该载面上的剪力、弯矩(图中的竖标)相叠加。因此,悬臂梁在q、F共同作用下的剪力、弯矩图,等于该简支梁单独在集中力F和均布荷载q作用下的代数和,如图8.27(d)、(g)所示。

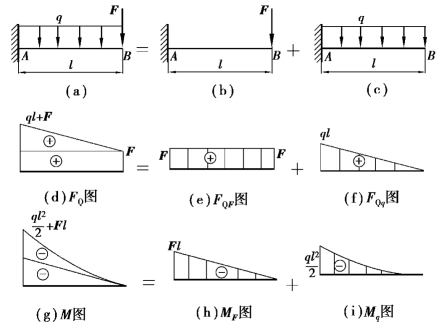
图8.27

【例8.15】　试用叠加法作如图8.28(a)所示简支梁的弯矩图。

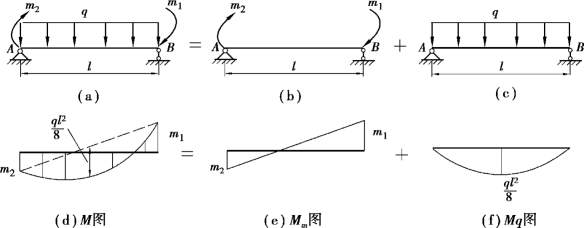
图8.28

【解】　当梁的两端分别有集中力偶m1,m2作用时,弯矩图如图8.28(e)所示,在均布荷载q作用下的弯矩图如图8.28(f)所示。其中对纵坐标具有不同正、负号的部分,叠加后图形重叠部分表示两个纵坐标值互相抵消,不重叠的部分即为所求的弯矩图。

有时用叠加法作梁的内力图是比较简单的。